Лекция 4. Теория множеств. Эквивалентные множества. Теорема Шрёдера -- Бернштейна. Мощность множества. Счётные множества и множества мощности континуума.

Теорию множеств называют фундаментом математики. На основе теоретико-множественных понятий формируются обычно все остальные математические понятия. Например, в элементарной математике рассматриваются множество точек и множество прямых, элементы которых связаны некоторыми соотношениями. При этом соотношение между точками – это бинарное отношение на т.е. подмножество множества соотношение между прямыми – подмножество множества а соотношение между точкой и прямой – это подмножество множества Далее, функция это отображение одного множества в другое (здесь область определения функции). В разных разделах математики часто используются операции над множествами – пересечение объединение разность Однако, для многих современных разделов математики (и, в частности, в нашем курсе математической логики) совершенно недостаточно лишь элементарных понятий и фактов теории множеств, а требуются более глубокие её результаты.

Основные идеи теории множеств были заложены немецким математиком Георгом Кантором в середине XIX века. В конце XIX – начале XX века было создано учение о мощности множества, сформулирован принцип трансфинитной индукции и были придуманы многие конструкции, без которых современная математика немыслима. Однако, вскоре в стройном здании теории множеств обнаружились трещины – логические противоречия, называемые антиномиями теории множеств. Устранить эти противоречия была призвана аксиоматическая теория множеств. Первой системой аксиом теории множеств была система аксиом Цермело – Френкеля (ZF), затем появилась система аксиом Гёделя – Бернайса (GB) и другие аксиоматические системы. Система GB основана на идее различения понятия “множество” и “класс” (грубо говоря, не всякая совокупность объектов имеет право называться множеством, запрещается существование таких “множеств”, как, например, “множество всех множеств”). Аксиоматизация теории множеств выдвинула такие вопросы, как независимость аксиом, непротиворечивость, полнота системы аксиом, т.е. чисто логические вопросы.

Мощность множества

Мощностью конечного множества мы будем называть количество его элементов. Оказывается, по количеству элементов можно сравнивать и бесконечные множества, т.е. не все бесконечные множества имеют одинаковое количество элементов. Точные формулировки мы дадим позже. Для конечного множества его мощность (т.е. количество элементов) обозначим Это число принадлежит множеству – расширенному множеству натуральных чисел. Чтобы изложение было целиком теоретико-множественным, нам надо дать определение натурального числа в терминах теории множеств. Это делается индуктивно:

число 0 – это множество (пустое множество);

число 1 – это множество (состоящее из одного элемента);

число 2 – это множество

и т.д.

То есть Отсюда, конечно, следует, что

Не определяя пока “количество элементов” бесконечного множества, мы можем легко определить, что значит, что два множества “состоят из одинакового количества элементов”.

Определение. Множества и называются эквивалентными (или равномощными), если существует взаимно однозначное отображение множества на множество

Для эквивалентных множеств мы будем писать или

Свойства эквивалентности множеств

1. 

2. если то

3. если а то

Определение. Мощностью множества называется совокупность всех множеств, эквивалентных множеству

Мощность множества обозначается

Теперь нам надо научиться сравнивать множества по мощности.

Определение. Говорят, что мощность множества не превосходит мощности множества (записываем: если существует вложение множества в множество Если существует вложение в но не существует взаимно однозначного отображения на то мы говорим, что мощность множества строго меньше мощности множества и пишем

Очевидны следующие свойства:

1. 

2. 

Гораздо менее очевидным является следующее свойство, называемое теоремой Шрёдера – Бернштейна:

Теорема 1 (теорема Шрёдера – Бернштейна). Если существуют вложения и то существует взаимно однозначное отображение

Эта теорема, наряду с теоретическим, имеет большое практическое значение. Она позволяет доказывать эквивалентность множеств и не строя взаимно однозначного отображения а построив лишь вложения и

Пример. Отрезок и интервал равномощны.

Действительно, тождественное отображение является вложением в Далее, отрезок вкладывается в интервал а он взаимно однозначно отображается на интервал с помощью отображения Отсюда по теореме Шрёдера – Бернштейна получаем:

Итак, отношение обладает обычными свойствами частичного порядка (рефлексивность, транзитивность, антисимметричность). Возникает вопрос: любые ли два множества сравнимы по мощности? Другими словами, верно ли, что для любых множеств и хотя бы одно из них вкладывается в другое? Ответ здесь положительный: для любых множеств А и В имеет место хотя бы одно из следующих соотношений: но доказать это мы сможем лишь позже – в разделе 2.2.

Счётные множества

Определение. Множество называется счётным, если

Например, счётным является множество чётных натуральных чисел. Действительно, отображение задаёт взаимно однозначное соответствие между множествами и

Свойства счётных множеств:

1. объединение двух счётных множеств счётно;

2. прямое произведение двух счётных множеств счётно;

3. объединение счётного числа счётных множеств счётно;

4. всякое бесконечное множество имеет счётное подмножество.

Доказательство. Докажем вначале утверждение 2). Пусть где счётные множества. Элементы множества можно расположить в виде таблицы:

			. . .
			. . .
			. . .
. . .	. . .	. . .	. . .

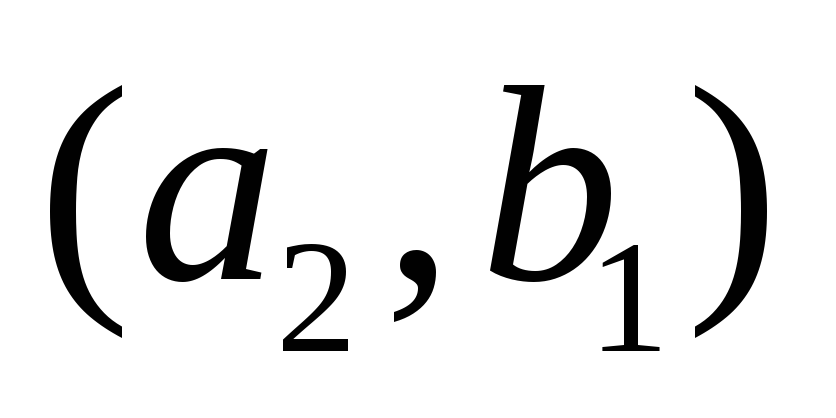
Пересчёт элементов множества т.е. установление взаимно однозначного соответствия между элементами множеств и может быть осуществлён, например, так:

1	2	4	7	11	16 . . .
3	5	8	12	17	23 . . .
6	9	13	18	24	31 . . .
10	14	19	25	32	40 . . .
15	20	25	33	41	50 . . .
21 . . .	27 . . .	34 . . .	42 . . .	51 . . .	. . . . . . . . .

Номер, который будет присвоен паре равен

Утверждение 3) следует из 2) и теоремы Шрёдера – Бернштейна. Поясним это. Пусть где каждое счётно. Так как вкладывается в то вкладывается в Осталось построить вложение По условию счётные множества, поэтому значит, элемент из имеет вид Не исключается, что при каких-нибудь Для каждого выберем одно какое-нибудь представление в виде Отображение определяет вложение в а по свойству 2) Значит,

Утверждение 1) следует из 3), так как

Докажем утверждение 4). Пусть бесконечное множество. Выберем элемент Так как бесконечно, то Значит, существует элемент Таким же образом найдём и т.д. Мы получили счётное подмножество множества

Мощность множества (а значит, любого счётного множества) обозначается (читается: “алеф-нуль”). Так как всякое бесконечное множество содержит счётное подмножество, то – самая маленькая из всех бесконечных мощностей.

Если и – два непересекающихся счётных множества, то по свойству 1) Это можно записать так: Аналогично этому свойство 2) можно записать так:

Определение. Множество называется несчётным, если оно бесконечно и неэквивалентно счётному множеству (т.е. его мощность больше ).

Следующая теорема принадлежит Г.Кантору.

Теорема 2 (Кантор). Множество несчётно.

Замечание. Приведённый здесь метод доказательства называется диагональным методом Кантора.

Определение. Мощность множества чисел отрезка называется мощностью континуума и обозначается с.

Очевидно, с

Свойства множеств мощности континуума

1) с + с = с; 2) с  с = с; 3) с + = с  = с.

4