Логика / lect1_m1_vm1_vt_lta_230100.62_niy06

Лекция 1.

Предмет математической логики. Язык исчисления высказываний. Формулы, секвенции, правила вывода, доказательства

Предмет математической логики. Необходимость изучения логики и теории алгоритмов. Машинное доказательство теорем. Понятие о недоказуемости. Непротиворечивость и модели. Пример: геометрия Лобачевского.

Синтаксис формальных языков

Алфавитом называется непустое множество. Его элементы называются символами или буквами. Конечные последовательности символов называются словами над алфавитом (включая пустую последовательность, которая обозначается Множество всех слов над алфавитом обозначается Языком над алфавитом называется подмножество

Замечание о метаязыке: Поскольку предметом изучения логики являются формальные языки, нам нужен язык, на котором мы могли бы говорить об этих языках (так называемый метаязык). В данном выше определении фигурируют символы Сами эти символы не являются выражениями и не принадлежат языку выражений. Это метапеременные, вместо которых можно подставить любое «натуральное число» (в смысле пунктов 1 и 2!) и арифметическое выражение соответственно. Вы уже знакомы с подобными примерами из анализа ( как метапеременные для функций), из алгебры ( как метапеременная для групп) и других разделов математики. Для каждой метапеременной, которую мы вводим, мы можем использовать верхние и нижние индексы, чтобы получить другие метапеременные того же типа.

Синтаксис ИВ. Формулы, секвенции

Алфавит ИВ содержит следующие символы:

1. пропозициональные переменные счётное множество пропозициональных переменных обозначается

2. символ абсурда

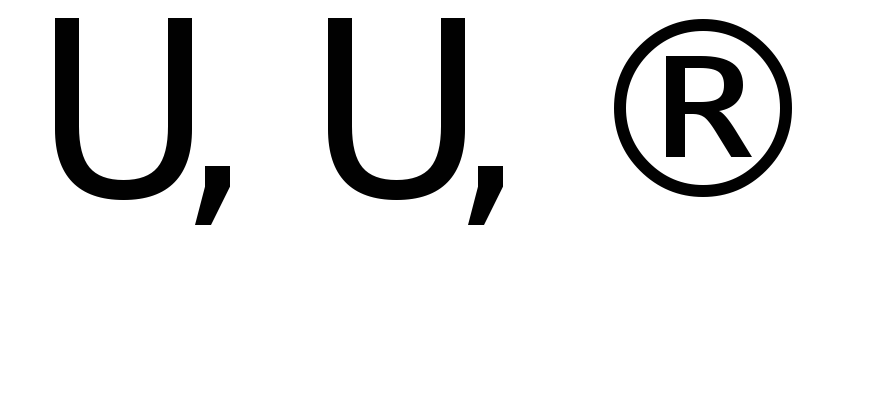3. логические связки: (одноместная) и (двухместные);

4. служебные символы: “(“, “)”, “,” (левая скобка, правая скобка, запятая);

5. символ

Атомарные формулы ИВ – это пропозициональные переменные и Множество атомарных формул обозначается

Множество формул ИВ – это множество, порожденное множеством атомарных формул и следующими операциями:

1. если – формула, то – формула;

2. если и – формулы, а – двухместная логическая связка, то – формула.

То есть в виде грамматики, используя метапеременные

Например, – формулы, а – не формулы.

Подформулой формулы мы будем называть любое подслово слова которое само является формулой. У одной подформулы может быть несколько вхождений в разных местах формулы

Длина формулыопределяется по рекурсии:

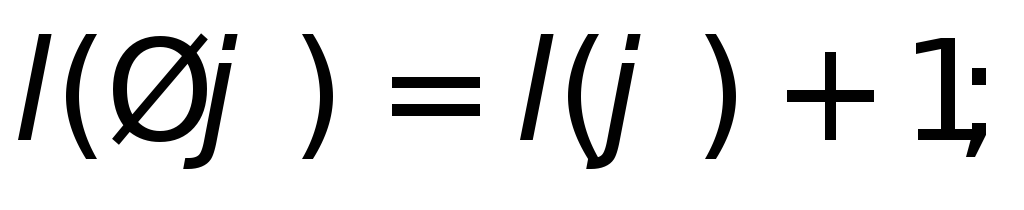1. 2) 3)

Лемма 1. Если и – формулы и – начало то

Доказательство проводится индукцией по построению формулы

Теорема 2 (об однозначности разбора). Всякая неатомарная формула единственным образом представима в одном из следующих видов: Соответствующая связка называется главной связкой а и – главными подформулами.

Из теоремы 2 следует, что существует алгоритм, определяющий по слову, записанному в алфавите ИВ, является ли оно формулой.

Объяснить, почему в неатомарных формулах необходимы внешние скобки.

Псевдосеквенциями называются записи вида где – множество формул ИВ (возможно, пустое), знак читается как «выводится». называется контекстом псевдосеквенции, а – ее заключением. Элементы называются гипотезами.

Вместо мы будем писать Кроме того, в записи контекста мы будем опускать фигурные скобки и использовать , как символ объединения (например, -- то же самое, что а -- то же самое, что Секвенция – это псевдосеквенция с конечным контекстом.

Множество секвенций обозначается множество псевдосеквенций – будет метапеременной для секвенций, – для псевдосеквенций.

Псевдовыражением называется формула, множество формул или псевдосеквенция. Конечное псевдовыражение называется выражением. и – обозначения множества и метапеременной для псевдовыражений соответственно.

Семантика ИВ

Интерпретации формул и секвенций

Всякое высказывание в классическом ИВ может быть истинно или ложно. Будем обозначать истину 1, а ложь 0. Множество значений истинности

Оценкой набора переменных называется функция Интерпретацией, соответствующей оценке называется функция такая, что

1. 2) 3) 4)

5) (считается, что 6)

Каждой оценке соответствует единственная интерпретация.

Будем говорить, что псевдовыражение истинно (соответственно, ложно) при оценке если (соответственно, В этом случае пишем (соответственно,

Тогда псевдосеквенция истинна при оценке если при этой оценке либо хотя бы одно ложно, либо истинно. Отсюда получается, что ложна при оценке если при этой оценке все истинны, а ложно.

называется тождественно истинным или общезначимым, если оно истинно при любой оценке, и выполнимым, если оно истинно при некоторой оценке.

Нетрудно увидеть, что тождественная истинность (выполнимость) формулы равносильна тождественной истинности (выполнимости) секвенции

Если псевдосеквенция тождественно истинна, будем писать К знаку относятся все вышеприведённые договорённости относительно знака

Формула называется следствием множества гипотез если

Оценка, на которой ложно, называется контрпримером для

Эквивалентность формул

Формулы и называются эквивалентными (обозначается: если и

Теорема о замене. Если и то

Следствие. Если то

Некоторые важные эквивалентности (это вовсе не исчерпывающий список!):

Законы поглощения:

Закон двойного отрицания:

Законы коммутативности:

Законы ассоциативности:

Законы дистрибутивности:

Законы де Моргана:

Законы импликации:

Эти эквивалентности можно доказать, либо составив таблицы истинности, либо проведя простые вычисления.