
Логика / lect3_m1_vm1_vt_lta_230100.62_niy06
.docЛекция 3. Интуиционистская логика
Обнаружившиеся в математике к началу ХХ века противоречия (см. раздел 2.4: антиномии теории множеств) вызвали естественное желание разобраться в причинах этих противоречий и устранить их. Голландский математик Брауэр решил, что причина проблемы в слишком абстрактном подходе к математике и отходе логических связок от их интуитивного понимания. В частности, он считал, что утверждать, что формула истинна, можно только предъявив ее доказательство; причем доказательства неатомарных формул строятся из доказательств подформул следующим образом:
![]() Чтобы
доказать
Чтобы
доказать
![]() необходимо доказать
необходимо доказать
![]() и
и
![]()
![]() Чтобы
доказать
Чтобы
доказать
![]() необходимо либо доказать
необходимо либо доказать
![]() либо доказать
либо доказать
![]()
![]() Чтобы
доказать
Чтобы
доказать
![]() необходимо найти способ превратить
любое доказательство
необходимо найти способ превратить
любое доказательство
![]() в доказательство
в доказательство
![]()
![]() Доказательства
Доказательства
![]() не существует.
не существует.
![]()
![]() понимается
как
понимается
как
![]() то есть, чтобы доказать
то есть, чтобы доказать
![]() необходимо доказать, что у формулы
необходимо доказать, что у формулы
![]() нет доказательства.
нет доказательства.
Введем
обозначение
![]() для множества доказательств
для множества доказательств
![]() Тогда вышесказанное можем перефразировать
так:
Тогда вышесказанное можем перефразировать
так:
![]()
![]()
![]()
![]()
![]()
![]() (множество
конструктивных
функций,
то есть функций, заданных некоторым
алгоритмом, из
(множество
конструктивных
функций,
то есть функций, заданных некоторым
алгоритмом, из
![]() в
в
![]()
![]()
![]()
![]()
![]()
Теперь
мы можем писать
![]() вместо «
вместо «![]() -- доказательство
-- доказательство
![]() ».
».
Примеры. Теперь мы можем рассмотреть несколько формул с интуиционистской точки зрения:
-
 Пусть
Пусть
 Тогда
Тогда
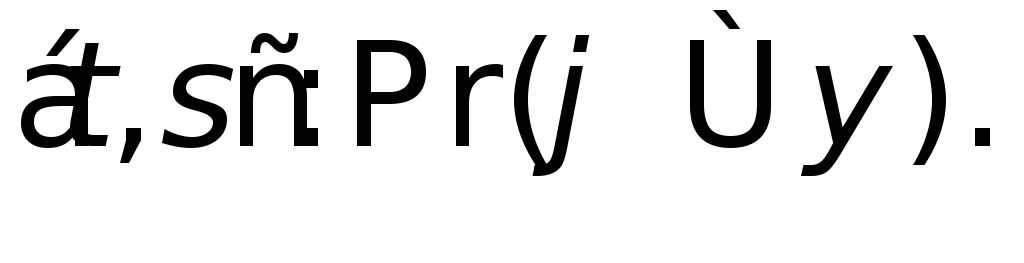 Определим следующую функцию
Определим следующую функцию

 В частности,
В частности,
 Тогда легко видеть, что
Тогда легко видеть, что
 то есть
то есть
 – доказательство искомой формулы.
– доказательство искомой формулы. -
 Пусть
Пусть
 По определению это функция, преобразующая
любое доказательство
По определению это функция, преобразующая
любое доказательство
 формулы
формулы
 в доказательство
в доказательство
 формулы
формулы
 То есть,
То есть,
 Нам нужно построить доказательство
формулы
Нам нужно построить доказательство
формулы
 то есть функцию
то есть функцию
 из
из
 в
в
 Но такую функцию можно определить как
Но такую функцию можно определить как
 Поэтому формула
Поэтому формула
 доказуема.
доказуема. -
 А
вот этого доказать нельзя. Чтобы доказать
А
вот этого доказать нельзя. Чтобы доказать
 нужно доказать одну из формул
нужно доказать одну из формул
 или
или
 Таким образом, чтобы убедить интуициониста
в доказуемости
Таким образом, чтобы убедить интуициониста
в доказуемости
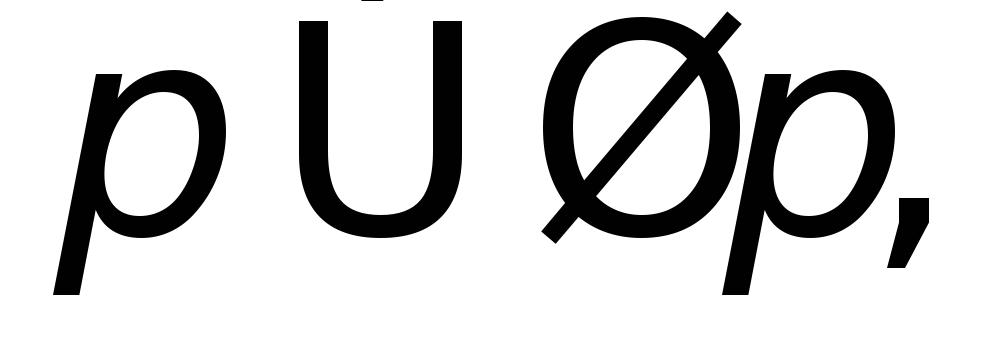 нужно найти единый способ, позволяющий
за конечное время решить любую
математическую задачу! Очевидно, такого
способа не существует.
нужно найти единый способ, позволяющий
за конечное время решить любую
математическую задачу! Очевидно, такого
способа не существует.
Для
формализации интуиционистского
исчисления высказываний воспользуемся
натуральной дедукцией. Из рассуждений,
подобных вышеприведённым, мы можем
убедиться, что почти все правила НД
корректны с интуиционистской точки
зрения. Например, рассмотрим правило
![]() Если у нас есть доказательство
Если у нас есть доказательство
![]() посылки
посылки
![]() и доказательство
и доказательство
![]() посылки
посылки
![]() то
то
![]() является доказательством заключения
является доказательством заключения
![]()
Единственное
правило НД, недопустимое с точки зрения
интуиционизма, это
![]() В самом деле, посылку
В самом деле, посылку
![]() следует понимать так: «нельзя доказать,
что
следует понимать так: «нельзя доказать,
что
![]() нельзя доказать». Но это никак не
позволяет нам найти доказательство
формулы
нельзя доказать». Но это никак не
позволяет нам найти доказательство
формулы
![]()
Многие теоремы классической логики верны и в интуиционистской логике. Кроме уже вышеприведённых это, например:
Выводы
для них всех без применения
![]() легко построить.
легко построить.
Примеры теорем классической логики, невыводимых в ИИВ:
Разумеется,
при подстановке вместо переменных
неатомарных формул может получиться
выводимый результат, например,
![]()
Итак,
в интуиционистской логике двойное
отрицание неэквивалентно отсутствию
отрицания. Однако тройное отрицание
эквивалентно однократному. Действительно,
![]() будет частным случаем
будет частным случаем
![]() а
а
![]() – частным случаем
– частным случаем
![]() Так как
Так как
![]() уже доказано, то по modus ponens получим:
уже доказано, то по modus ponens получим:
![]() а отсюда
а отсюда
![]()
Докажем
теперь невыводимость секвенции
![]() (закона
исключённого третьего)
в интуиционистской логике формально.
Рассмотрим трёхзначное множество
значений истинности
(закона
исключённого третьего)
в интуиционистской логике формально.
Рассмотрим трёхзначное множество
значений истинности
![]() в котором 0 интерпретируется как ложь,
1 – как истина,
в котором 0 интерпретируется как ложь,
1 – как истина,
![]() – как неопределённость. Определим
логические операции на
– как неопределённость. Определим
логические операции на
![]() следующим образом:
следующим образом:
![]()
![]()
![]()
![]()
![]()
Понятия
оценки и интерпретации на
![]() вводятся по аналогии с
вводятся по аналогии с
![]() Назовем секвенцию
Назовем секвенцию
![]() истинной при оценке
истинной при оценке
![]() если
если
![]() и тождественно истинной в трёхзначной
логике, если она истинна при всех оценках.
Можно проверить, что все правила НД,
кроме
и тождественно истинной в трёхзначной
логике, если она истинна при всех оценках.
Можно проверить, что все правила НД,
кроме
![]() корректны на
корректны на
![]() (то есть из тождественно истинных в
(то есть из тождественно истинных в
![]() посылок получаются тождественно истинные
заключения). Кроме того, аксиомы
тождественно истинны. Значит, все
выводимые в ИИВ формулы тождественно
истинны в
посылок получаются тождественно истинные
заключения). Кроме того, аксиомы
тождественно истинны. Значит, все
выводимые в ИИВ формулы тождественно
истинны в
![]() Однако, формула
Однако, формула
![]() тождественно истинной не является, так
как при
тождественно истинной не является, так
как при
![]()
![]() Значит, формула
Значит, формула
![]() невыводима в ИИВ.
невыводима в ИИВ.
Замечание.
Существуют тождественно истинные в
трёхзначной логике, но невыводимые в
ИИВ формулы. Например,
![]()
![]() Более того, никакой конечный набор
значений истинности не полон для ИИВ.
Более того, никакой конечный набор
значений истинности не полон для ИИВ.
Задачи для самостоятельного решения
-
Доказать выводимость в ИИВ формулы

-
Доказать невыводимость в ИИВ формул:
