Логика / lect15_m2_vm1_vt_lta_230100.62_niy06

Лекция 15. Существование перечислимого неразрешимого множества. Алгоритмически неразрешимые задачи

Теорема 6. Существует вычислимая функция от которой никакая вычислимая функция одного аргумента не может отличаться во всех точках, т.е. для любой вычислимой функции найдётся такое N, что

Теорема 7. Существует вычислимая функция, не имеющая всюду определённого вычислимого продолжения.

Теорема 8. Существует перечислимое неразрешимое множество натуральных чисел.

Будем говорить, что для машины Тьюринга проблема остановки алгоритмически разрешима, если существует другая машина Тьюринга которая для каждого натурального числа выясняет, остановится или не остановится машина имея на входе число Для определённости пусть имея на входе число выдаёт на выходе 1, если останавливается (будучи запущенной на ленте, на которой написано число и выдаёт на выходе 0, если не останавливается.

Теорема 9. Существует машина Тьюринга для которой проблема остановки алгоритмически неразрешима.

Задачи для самостоятельного решения

1. Доказать, что всякое конечное множество разрешимо.

2. Доказать, что функция вычислима. (Здесь [ ] обозначает целую часть числа).

Указание: воспользоваться равенством

3. Является ли разрешимым:

а) множество всех простых чисел;

б) множество N}?

Ответ: а) да; б) да.

Указание: воспользоваться равенством

4. Даны два пересекающихся перечислимых множества и Доказать, что существуют непересекающиеся перечислимые множества и такие, что

5. Доказать, что всякое бесконечное перечислимое множество можно записать в виде где 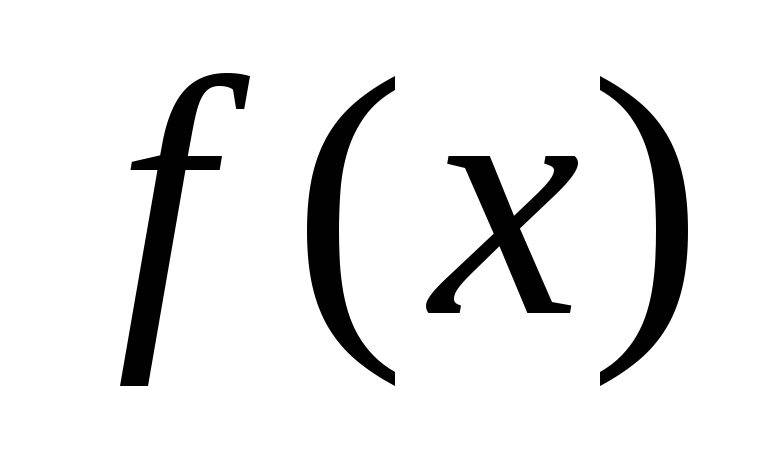– вычислимая функция, все значения которой различны.

6. Доказать, что всякое бесконечное перечислимое множество содержит бесконечное разрешимое подмножество.

Указание: воспользоваться результатом предыдущей задачи.

7. Пусть и – множества натуральных чисел такие, что Доказать, что разрешимо (соотв., перечислимо) в том и только том случае, если разрешимо (соотв., перечислимо).

Алгоритмически неразрешимые задачи

В разных разделах математики встречаются алгоритмически неразрешимые задачи, т.е. задачи, для которых нет алгоритма решения, причём нет не потому что его пока не придумали, а потому что он невозможен в принципе. Разумеется, алгоритм надо понимать в смысле машин Тьюринга и рекурсивных функций (см. разделы 4.1-4.4). Сформулируем некоторые из этих задач. Доказывать их алгоритмическую неразрешимость мы не будем, так как это выходит за рамки данного пособия.

Проблема остановки машины Тьюринга. В теореме 9 предыдущего раздела было доказано существование машины Тьюринга с неразрешимой проблемой остановки. Постановку задачи о неразрешимости проблемы остановки можно несколько расширить. Машина Тьюринга – это объект, определяемый конечным числом параметров. Все частичные отображения одного конечного множества в другое могут быть эффективным образом перенумерованы. Поэтому каждой машине Тьюринга можно присвоить номер (натуральное число). Пусть машина Тьюринга с номером Некоторые машины, начинающие работать на пустой ленте, в конце концов останавливаются, а некоторые работают бесконечно долго. Возникает задача: по натуральному числу определить, остановится или нет машина Тьюринга запущенная на пустой ленте. Эта задача алгоритмически неразрешима. То есть не существует автоматической процедуры, для каждого решающей, останавливается или нет машина Это не исключает того, что для какой-либо конкретной машины мы установим, останавливается она или нет. Не существует метода, решающего это сразу для всех машин.

Проблема равенства слов. Группы и полугруппы часто задаются образующими элементами и определяющими соотношениями. Например, группа подстановок на трёхэлементном множестве имеет образующие элементы и и определяющие соотношения Каждый элемент из является произведением элементов и взятых, возможно, несколько раз, т.е. словом в алфавите причём это слово в общем случае не единственно. Например, и один и тот же элемент из Возникает вопрос: равны два данных слова в группе или нет? Существует ли алгоритм, решающий этот вопрос для любых двух слов? Для группы ответ положительный: алгоритм существует, и читатель сформулирует его без труда. Однако, существуют полугруппы (и группы), для которых такого алгоритма нет. Итак, пусть полугруппа задана образующими элементами и соотношениями ( слова от ), то в общем случае не существует алгоритма, определяющего для двух произвольных слов равны они как элементы из или не равны (т.е. следует равенство из равенств или не следует). Кроме того, в общем случае алгоритмически неразрешим вопрос о том, будет ли полугруппа конечной (или коммутативной, или периодической).

Проблема истинности формулы. Всякая аксиоматическая теория определяется наличием аксиом и правил вывода утверждений из аксиом. Будем считать, что тех и других конечное число. Утверждения, выводимые из аксиом, называются теоремами. Пусть дана правильно построенная формула Является ли теоремой, т.е. выводима ли из аксиом Существуют аксиоматические теории, для которых выяснить для произвольной формулы является ли она теоремой, алгоритмически неразрешимо.

Проблема существования решения диофантова уравнения. Диофантовым уравнением называется уравнение в целых числах, т.е. уравнение вида где – многочлен с целыми коэффициентами. Оказывается, что существуют такие многочлены для которых не существует алгоритма определения для каждого натурального числа имеет или не имеет целочисленных решений уравнение