
Моделирова / Отчёт
.docxЗадание 1
Часть «а»
Вход – сила F, выход - координата
Дифференциальное уравнение

Передаточная функция

Весовая функция
>> m=8;p=0.6;k=12;
>> syms s
>> W=1/(m*s^2+p*s+k);
>> ilaplace(W)
ans =
(10*9591^(1/2)*sin((9591^(1/2)*t)/80))/(9591*exp((3*t)/80))
>> vpa(ans,5)
ans =
(0.10211*sin(1.2242*t))/exp(0.037500000000001421085471520200372*t)
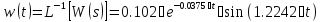
Описание в пространстве состояний


Моделирование в MATLAB
m=8;
p=0.6;
k=12;
A=[0 1; -k/m -p/m]; B=[0; 1/m]; C=[1 0]; D=0;
M=ss(A, B, C, D);
tf(M)
subplot(211)
step(M)
subplot(212)
impulse(M)

Часть «б»
Вход – ток i; Выход – напряжение на всех элементах(соединены параллельно)
Дифференциальное уравнение

Передаточная функция

Весовая функция
r=0.6;
l=8;
c=12;
syms s;
W=s/(s^2*c+s*1/r+1/l);
vpa(ilaplace(W), 5)
(0.083333*(cos(0.074794*t) - 0.92848*sin(0.074794*t)))/exp(0.069444444444442865460587199777365*t)

Описание в пространстве состояний


Моделирование в MATLAB
r=0.6;
l=8;
c=12;
A=[0 1/l; -1/c -1/(r*c)]; B=[0; 1/c]; C=[0 1]; D=0;
M=ss(A, B, C, D);
tf(M)
subplot(211)
step(M)
subplot(212)
impulse(M)

Часть «в»
Вход - напряжение на источнике. Выход – ток в цепи
Дифференциальное уравнение

Передаточная функция

Весовая функция
r=0.6;
l=8;
c=12;
syms s;
W=s/(s^2*l+s*r+1/c);
vpa(ilaplace(W), 3)
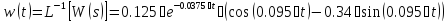
Описание в пространстве состояний

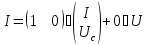
Моделирование в среде MATLAB
r=0.6;
l=8;
c=12;
A=[-r/l -1/l; 1/c 0]; B=[1/l; 0]; C=[1 0]; D=0;
M=ss(A, B, C, D);
tf(M)
subplot(211)
step(M)
subplot(212)
impulse(M)

Задание 2
Часть «а»
>> dsolve('D3x+D2x+Dx+x=0, x(0)=1, D3x(0)=1, Dx(0)=-2')
ans =
1/(2*exp(t)) + cos(t)/2 - (3*sin(t))/2
>> S=ans;
>> diff(S,3)+diff(S, 2)+diff(S)+S
ans =
0
>> subs(diff(S), 0)
ans =
-2
Часть «б»
>> dsolve('D3x+D2x+Dx+x=0, x(0)=60, Dx(0)=0, D3x(0)=0')
ans =
60*cos(t)
Задание 3
Часть «а»
>> dsolve('D3x-2*Dx+Dx=4, x(0)=1, Dx(0)=2, D2x(0)=-2')
ans =
2*exp(t) - 4/exp(t) - 4*t + 3
Часть «б»
>> dsolve('D2x+n^2*x=a*sin(n*t+a), x(0)=0, Dx(0)=0')
ans =
- (1/exp(n*t*i))*((a*t*(1/exp(a*i)))/(4*n) + (a*exp(a*i)*exp(2*n*t*i)*i)/(8*n^2)) - exp(n*t*i)*((a*t*exp(a*i))/(4*n) - (a*(1/exp(a*i))*(1/exp(2*n*t*i))*i)/(8*n^2)) - (a*(1/exp(a*i))*exp(n*t*i)*i)/(8*n^2) + (a*exp(a*i)*(1/exp(n*t*i))*i)/(8*n^2)
Задание 4
syms t s a b l
X_t=exp(-l*t);
W_s=1/(a*s+b);
X_s=laplace(X_t);
Y_s=W_s*X_s;
Y_t=ilaplace(Y_s)
tmax=solve(diff(Y_t, t), t)
DATANAME={'a', 'b', 'T', 'l'};
DATAVAL = {1, 2, 3, 0.8};
W_s_=subs(W_s, DATANAME, DATAVAL);
[num, den] = numden(W_s_);
num_c = fliplr(double(coeffs(num, s)));
den_c = fliplr(double(coeffs(den, s)));
M=tf(num_c, den_c);
X_t_f=matlabFunction(subs(X_t, DATANAME, DATAVAL));
t=0:0.1:10;
X_t_v = X_t_f(t);
lsim(M, X_t_v, t);

Задание 5
>> S=dsolve('D4y-y=exp(-t), y(0)=3, Dy(0)=-5.25, D2y(0)=7.5, D3y(0)=-5.75');
>> simplify(S)
ans =
5*exp(-t) - 2*cos(t) - (t*exp(-t))/4

odefun=@(t, X)((diag([1 1 1], 1)+diag([1],-3))*X+exp(-t)*[0 0 0 1]');
Y0=[3 -5.25 7.5 -5.75]';
tspan=[0 15];
solve=@(t)(5*exp(-t) - 2*cos(t) - (t*exp(-t))/4);
close all
figure
fplot(solve, tspan,'k')
hold on
Y23=ode23(odefun, tspan, Y0);
Y45=ode45(odefun, tspan, Y0);
Y15=ode15s(odefun, tspan, Y0);
plot(Y23.x, Y23.y(1, :), ...
Y45.x, Y45.y(1, :), ...
Y15.x, Y15.y(1, :))
legend('A', '23', '45', '15')
grid on

