
- •Введение
- •1.2. Принципы автоматического управления
- •1.3. Классификация математических моделей динамических систем
- •1.4. Типовые входные воздействия, их представление во временной и комплексной областях, практическое применение
- •1.6. Частотные характеристики линейных динамических систем
- •1.7. Экспериментальное определение частотных характеристик линейной динамической системы
- •1.8. Передаточная функция линейной динамической системы и ее свойства
- •2.1. Общая характеристика типовых звеньев и их классификация
- •2.2. Апериодическое звено
- •2.4. Дифференцирующее звено первого порядка
- •2.5. Безынерционное звено
- •2.6. Интегрирующее звено
- •2.7. Идеальное дифференцирующее звено
- •2.8. Колебательное звено
- •2.9. Дифференцирующее звено второго порядка
- •2.10. Запаздывающее звено
- •2.12. Методика построения ЛЧХ сложных САУ
- •Глава 3. Структурные схемы и передаточные функции автоматических систем
- •3.2. Функциональная схема замкнутой САУ, назначение отдельных устройств и элементов. Классификация САУ
- •3.4. Правила преобразования структурных схем
- •3.5. Примеры преобразования структурной схемы сложной динамической системы
- •Глава 4. Устойчивость систем автоматического управления
- •4.1. Понятие устойчивости. Устойчивость и корни характеристического уравнения
- •4.2. Алгебраический критерий устойчивости Рауса – Гурвица
- •4.3. Критерий устойчивости Михайлова
- •4.4. Следствия из критерия Михайлова
- •4.5. Критерий устойчивости Найквиста
- •4.6. Применение критерия устойчивости Найквиста для астатических систем
- •4.7. Логарифмический критерий устойчивости
- •4.8. Запасы устойчивости по амплитуде и фазе
- •Литература
Входной величиной является смещение z(t) поршня гидравлического клапана (золотника) относительно нейтрального положения, а выходной - смещение x(t) поршня исполнительного цилиндра.
Сигнал z(t) вызывает смещение поршня гидравлического клапана и, следовательно, возникает перепад давления масла в левой и правой частях гидроцилиндра и соответственно движение поршня x(t) .
Так как p = const , то скорость перемещения поршня гидравлического цилиндра
t
пропорциональна степени открытия клапанов, т.е. x&(t) = kz(t) или x(t) = kòz(t)dt .
0
2.7. Идеальное дифференцирующее звено
Выходной сигнал дифференцирующего звена пропорционален производной от входного сигнала. Дифференциальное уравнение дифференцирующего звена:
a0 x(t) = b1z&(t) ; x(t) = kz&(t) ,
где k = b1  a0 .
a0 .
Возьмем преобразование Лапласа от обеих частей дифференциального уравнения при нулевых начальных условиях и определим передаточную функцию:
X (s) = ksZ(s) ;
W (s) = X (s) = ks . Z(s)
Заменив в передаточной функции s на jω , получим АФХ:
W ( jω) = kjω ;
U (ω) = 0 ;
V (ω) = jkω .
Найдем частотные характеристики дифференцирующего звена:
H (ω) = kω ;
ϕ(ω) = argtg V (ω) = arctg(+∞) = +π/ 2 . U (ω)
Графики соответствующих функций показаны на рис.2.41 и 2.42.
U(ω), V(ω)
V(ω)
0 |
ω |
U(ω)
Рис.2.41. Вещественная и мнимая
части АФХ идеального дифференцирующего звена для ω
60
H(ω) |
ϕ(ω) |
|||||
|
|
|
π/2 |
|
|
|
0 |
|
|
0 |
|
|
|
ω |
ω |
|||||
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2.42. Графики АЧХ и ФЧХ идеального дифференцирующего звена для w ³ 0
Годограф АФХ расположен на мнимой оси (рис.2.43). Для положительных частот
годограф совпадает с положительной частью мнимой полуоси: lim W ( jw) = ¥ ;
ω→∞
lim W ( jw) = 0 .
ω→0
V(w)
8 ω
0 ω
0 U(w)
Рис.2.43. Годограф идеального
дифференцирующего звена
ЛАЧХ дифференцирующего звена:
Lm (w) = 20lgkω = 20lgk + 20lgω .
Таким образом, ЛАЧХ соответствует прямая линия с наклоном +20 дБ/дек. Определим характерные точки ЛАЧХ. При k = 1 Lm (w) = +20lgω . Точка пересечения
ЛАЧХ с осью частот находится из уравнения Lm (w) = 0 , 20lgω = 0 , откуда ωc =1. Если k ¹ 1 , то из уравнения Lm (w) = 0 следует, что 20lg(kω) = 0 и ωc = 1 / k
(рис.2.44).
Lm(ω), дБ
+20 дБ/дек
|
|
|
|
lg ω |
|
|
|
|
|
|
|
1 |
|
|
|
ω, Гц |
|
|
ωc = 1/k |
||||
|
|||||
|
|||||
|
|||||
20lgk
Рис.2.44. График ЛАЧХ идеального
дифференцирующего звена
61

ЛФЧХ подобна ФЧХ и представляет собой прямую линию, проведенную на уровне
+π / 2.
Идеальное дифференцирующее звено хорошо пропускает высокочастотные сигналы и плохо - низкочастотные, т.е. является фильтром высоких частот.
В реальных условиях на вход дифференцирующего звена одновременно с полезным сигналом поступает помеха, которая, как правило, является высокочастотной. График ЛАЧХ имеет возрастающий характер, поэтому на выходе звена удельный вес помехи больше, чем полезного сигнала, что является недостатком применения этого звена в данной ситуации.
Приведем примеры реализации дифференцирующего звена. Пример 1. RC-цепочка (рис.2.45)
U1 |
C |
R |
U2 |
|
Рис.2.45. RC-цепочка - пример реализации
дифференцирующего звена
W (s) = U2 |
(s) |
= |
|
R |
= |
|
RCs |
= |
Ts |
|
, T = RC. |
|
||
|
|
|
1 |
|
RCs + 1 |
Ts + 1 |
|
|||||||
U1 |
(s) |
|
R |
|
|
|
|
|
|
|||||
|
|
|
+ sC |
|
|
|
|
|
|
|
|
|
||
Этой передаточной функции соответствует дифференциальное уравнение |
||||||||||||||
|
|
TU ′ |
(t) + U |
2 |
(t) = TU ′(t). |
|
|
|||||||
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
||
Очевидно, что RC-цепочка не является идеальным дифференцирующим звеном, |
||||||||||||||
′ |
|
|
|
|
|
|
|
|
|
|
|
|
′ |
(t) . |
однако при условии, что TU2 (t) << U2 |
(t) , можно считать, что U2 (t) = TU1 |
|||||||||||||
Пример 2. В качестве дифференцирующего элемента в САУ наряду с электронными дифференциаторами часто используют тахогенераторы (тахометры) постоянного тока. Они представляют собой малогабаритные электрические генераторы постоянного тока, применяемые для измерения угловой скорости вращения валов различных машин и механизмов (рис.2.46).
α(t) Uтг(t)
Uтг(t)
Рис.2.46. Тахогенератор - пример реализации
дифференцирующего звена
Входной величиной тахогенератора Выходная величина - напряжение Uтг(t). угловой скорости вала Ω(t).
является угол поворота |
якоря •(t). |
Это напряжение линейно |
зависит от |
62

Так как Ω(t) = dadt(t) , то Uтг(t) = = kΩ(t), или Uтг (t) = k dadt(t) .
Взяв преобразование Лапласа от обеих частей последнего равенства при нулевых начальных условиях, получим:
Uтг (s) = ksa(s);
W (s) = Uтг (s) = ks. a(s)
2.8. Колебательное звено
Колебательное звено является частным случаем звена второго порядка,
динамика которого описывается дифференциальным уравнением
a2&x&(t) + a1x&(t) + a0 x(t) = b0 z(t) .
Возьмем преобразование Лапласа от обеих частей дифференциального уравнения при нулевых начальных условиях:
a2 X (s) × s2 + a1sX (s) + a0 X (s) = b0Z(s); X (s) × (a2s2 + a1s + a0 ) = b0 z(s).
Следовательно, передаточная функция колебательного звена имеет вид:
W (s) = |
X (s) |
= |
b0 |
|
|
|
. |
||
Z(s) |
a2s2 + a1s + a0 |
|||
Во многих случаях (радиоэлектроника, электротехника, механика) бывает удобно
использовать дифференциальное уравнение колебательного звена в несколько ином виде:
T 2 &x&(t) + 2Txx&(t) + x(t) = kz(t) .
Между двумя формами записи дифференциального уравнения существует однозначное соответствие:
T = |
|
a2 |
|
|
, T |
- постоянная времени; |
||||
a0 |
||||||||||
|
|
|
|
|
|
|||||
x = |
|
|
|
a1 |
|
|
, ξ - относительный коэффициент затухания (коэффициент |
|||
2 |
|
|
|
|
a2 |
|||||
|
a0 |
|||||||||
демпфирования). В колебательном звене 0 < ξ < 1 ;
k = b0 - коэффициент передачи. a0
Второй форме записи дифференциального уравнения колебательного звена соответствует следующая передаточная функция:
W (s) = |
X (s) |
= |
k |
|
. |
(2.8) |
|
Z (s) |
T 2s2 + 2xTs +1 |
||||||
|
|
|
|
||||
Полюсами W ( jω) или корнями характеристического уравнения
T 2s2 + 2xTs +1 = 0
при 0 < ξ < 1 будут два комплексных числа:
63

|
|
|
|
s |
= |
- 2xT ± |
|
4x2T 2 - 4T 2 |
|
= |
- x ± |
|
|
x2 -1 |
= -b ± jw, |
(2.9) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1,2 |
|
|
|
2T 2 |
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где β - коэффициент, характеризующий скорость затухания колебаний звена, |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1- x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
b = |
= w x ; |
w = |
; |
w = w |
1- x2 = |
|
|
- собственная частота колебаний звена. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
T |
0 |
0 |
|
T |
1 |
0 |
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Переходная функция звена (реакция системы на единичную ступенчатую |
||||||||||||||||||||||||||||
функцию): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
é |
|
|
1 |
ù |
; |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
h(t) = L W (s) |
|
ú |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
s |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
û |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
é |
|
|
|
|
|
k |
|
|
|
1 |
ù |
|
|
|||
|
|
|
|
|
|
|
|
|
|
h(t) = |
L−1 ê |
|
|
|
|
|
|
|
|
|
|
ú . |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 2xTs +1 s |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ëT 2s |
2 |
|
û |
|
|
|||||||||
|
С учетом введенных обозначений |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
h(t) = k(t)é1 - e- βt (cosw t + |
|
|
b |
sin w t)ù . |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
1 |
|
|
w1 |
1 ú |
|
||||||
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
|
û |
|
||||||
Вид функции h(t) показан на рис.2.47.
h(t) 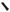
k
0 |
t |
Рис.2.47. Переходная функция
колебательного звена
Рассмотрим частотные характеристики колебательного звена. АФХ колебательного звена:
W ( jw) = |
|
|
k |
k |
|
||
|
|
= |
|
|
; |
||
- T 2w2 + 2xTjw +1 |
(1- T 2w2 ) + 2 jxTw |
||||||
|
U (w) = |
k(1- w2T 2 ) |
; |
|
|||
|
(1- T 2w2 )2 + (2xTw)2 |
|
|||||
|
V (w) = |
|
- 2kxTw |
. |
|
||
|
|
(1- T 2w2 )2 + (2xTw)2 |
|
||||
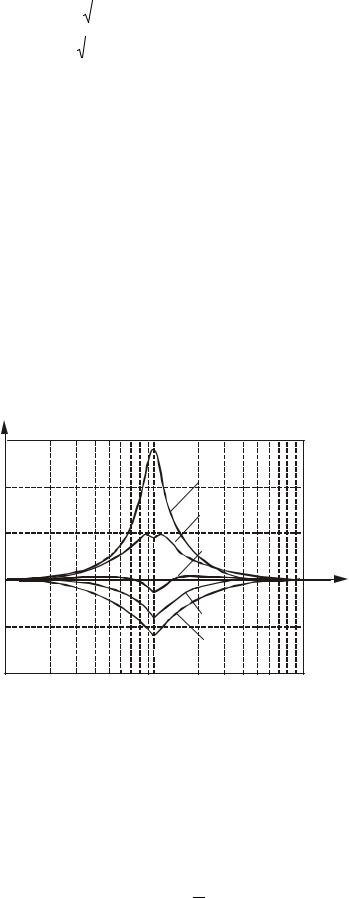
Графики вещественной и мнимой частей АФХ колебательных звеньев с различным соотношением относительных коэффициентов затухания ξ показаны на рис.2.48.
64
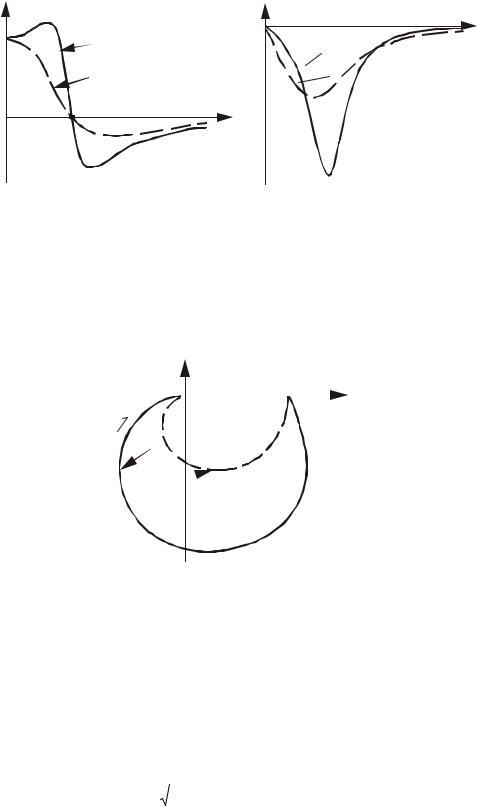
U(ω) |
|
V(ω) |
|
|
k |
1 |
0 |
1 1/T |
ω |
|
||||
|
|
|
||
|
2 |
|
2 |
|
|
|
|
|
|
0 |
1/T |
ω |
|
|
Рис.2.48. Вещественная и мнимая части АФХ колебательных звеньев: 1 - звено с относительным коэффициентом затухания ξ1; 2 - звено с относительным коэффициентом затухания ξ2 (ξ1 < ξ2)
На рис.2.49 представлено семейство кривых годографа АФХ колебательных звеньев при различных значениях ξ . Годограф при ω = 0 начинается на вещественной
оси, так как W (0) = k , и с ростом частоты от ω = 0 до ω = ∞ последовательно проходит четвертый и третий квадранты. С уменьшением ξ годограф расширяется ("разбухает").
|
|
jV |
k |
|
|
|
|
||
8 |
ω = 0 |
|
U |
|
|
|
|
|
|
ω |
1 |
|
|
|
2
Рис.2.49. Годографы колебательных звеньев при
различных значениях относительного коэффициента затухания ξ: 1 - звено с ξ1; 2 - звено с ξ2 (ξ1 < ξ2)
АЧХ колебательного звена можно получить обычным образом, но проще это сделать, рассматривая его передаточную функцию в виде дроби (см. § 2.1), в числителе которой записана передаточная функция усилительного звена (W1(s) = k ), а
в знаменателе - передаточная функция дифференцирующего звена второго порядка
(W2 (s) = T 2s2 + 2ξTs + 1): |
|
|
|
||
H (ω) = |
|
k |
|
. |
|
|
|
|
|||
(1− ω2T 2 )2 + (2ξTω)2 |
|||||
|
|
|
|
||
На частоте ω0 = 1/T при ξ = 0 колебания не затухают (рис.2.50). Колебательное звено, для которого ξ = 0 , называют консервативным звеном.
65

H(ω)
1
2
3
k
0 |
ω0 = 1/T |
ω |
||
Рис.2.50. График АЧХ
колебательного звена при различных значенияx
относительного коэффициента затухания: 1 - ξ = 0,05; 2 - ξ = 0,5; 3 - ξ = 0,7
ФЧХ колебательного звена найдем путем вычитания из ФЧХ усилительного звена ( j1(w) = 0 ) ФЧХ дифференцирующего звена второго порядка. В результате получим следующие формулы:
j(w) = -arctg |
|
2xTw |
при w < |
1 |
|
; |
|
|||||
|
|
|
T |
|
|
|||||||
1- w2T 2 |
|
|
|
|
1 |
|
||||||
j(w) = -p - arctg |
2xTw |
|
при w > |
; |
||||||||
1- w2T 2 |
T |
|||||||||||
|
|
|
1 |
|
|
|
||||||
ϕ(ω) = −π/ 2 при w = |
. |
|
|
|
|
|||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
T |
|
|
|
|
||
Колебательное звено вносит отрицательный сдвиг фаз между входным и выходным сигналами в пределах от ϕ = 0 при ω = 0 до ϕ = −π при ω → ∞ . При
w = w0 = 1/T независимо от ξ j(w0 ) = -π / 2. ЛАЧХ колебательного звена:
L m (w) = 20lgH (ω ); |
|
|
|||
Lm (ω ) = 20lg |
|
k |
|
; |
|
|
|
|
|||
(1-T 2w2 )2 + (2xTw)2 |
|||||
|
|
|
|
||
Lm (w) = 20lgk - 20lg
 (1-T 2w2 )2 + (2xTw)2 .
(1-T 2w2 )2 + (2xTw)2 .
При k =1 имеем Lm (w) = -20lg
 (1-T 2w2 )2 + (2xTw)2 .
(1-T 2w2 )2 + (2xTw)2 .
Определим низкочастотную и высокочастотную асимптоты ЛАЧХ. При малых значениях ω ( ω → 0 ) имеем:
|
é |
|
|
|
|
|
|
|
|
|
ù |
|
lim |
-20lg (1-T |
2 |
w |
2 |
) |
2 |
+ (2xTw) |
2 |
= -20lg1 = 0. |
|||
ê |
|
|
|
|
ú |
|||||||
ω→0 |
ë |
|
|
|
|
|
|
|
|
|
û |
|
Следовательно, низкочастотная асимптота ЛАЧХ приближается к оси абсцисс. При больших значениях ω ( ω → ∞ ) имеем:
Lm (w) = -20lg
 (1 -T 2w2 )2 + (2xTw)2 » -20lg
(1 -T 2w2 )2 + (2xTw)2 » -20lg 
 (1 -T 2w2 )2 = = -20lgT 2w2 = -40lgTw.
(1 -T 2w2 )2 = = -20lgT 2w2 = -40lgTw.
Поступив по аналогии с определением наклона ЛАЧХ апериодического звена (см. § 2.2), найдем, что наклон высокочастотной асимптоты ЛАЧХ колебательного звена составляет –40 дБ/дек. Точка пересечения низкочастотной и высокочастотной асимптот соответствует частоте wc = 1/T . На этой частоте имеет место максимальное отклонение
асимптотических ЛАЧХ от реальных. Его величина определяется по формуле
66
|
|
|
|
|
|
|
|
|
|
L m (ω) = −20lg |
|
(1−T 2ω2 )2 + (2ξTω)2 для ξ =1. |
|||
|
1 |
|
|
|
|||
При w = |
имеем: Lm (ω) = -20lg |
02 + (2×1×1)2 = -20lg2 » -6 дБ. |
|||||
T |
|||||||
|
|
|
|
|
|
||
В интервале частот вблизи ωc =1/T ЛАЧХ колебательного звена
не могут быть заменены прямолинейными асимптотами. Для уточнения асимптотических ЛАЧХ в окрестности частот, близких к частоте ωc =1/T , необходимо
ввести поправки L в зависимости от величины ξ . Поправки для некоторых значений ξ приведены в табл.2.2 и на рис.2.51.
Таблица 2.2
Таблица поправок L к асимптотическим ЛАЧХ колебательного звена
ξ |
|
|
ω/ω0 |
|
|
|
0,1 |
0,3 |
0,6 |
0,8 |
1,0 |
||
|
||||||
|
|
|
|
|
|
|
0,1 |
0,086 |
0,800 |
3,726 |
8,091 |
13,979 |
|
0,3 |
0,071 |
0,653 |
2,683 |
4,437 |
4,437 |
|
|
|
|
|
|
|
|
0,6 |
0,024 |
0,188 |
0,325 |
–0,217 |
–1,584 |
|
|
|
|
|
|
|
|
0,8 |
–0,025 |
–0,247 |
–1,242 |
–2,475 |
–4,082 |
|
|
|
|
|
|
|
|
1 |
–0,086 |
–0,749 |
–2,671 |
–4,297 |
–6,021 |
|
|
|
|
|
|
|
L, дБ |
|
|
15 |
|
|
10 |
x = 0,1 |
|
|
|
|
|
0,3 |
|
5 |
0,6 |
|
|
|
|
0 |
|
lg(ω) |
|
ω |
|
|
|
|
−5 |
0,8 |
|
1 |
|
|
|
|
|
−10 0,1 |
1 |
10 |
Рис.2.51. Графики поправок к асимптотическим ЛАЧХ |
||
|
колебательного звена |
|
Из графиков поправок видно, что скачок может быть вверх или вниз в зависимости от величины ξ . Поэтому для уточнения асимптотических ЛАЧХ удобно
применять комплект шаблонов, каждый из которых изготовлен для постоянного значения ξ .
ЛФЧХ колебательного звена подобна ее ФЧХ в обычном масштабе, но деформирована по оси частот. На частоте ωc = T1 при ξ = 0 ЛФЧХ получает
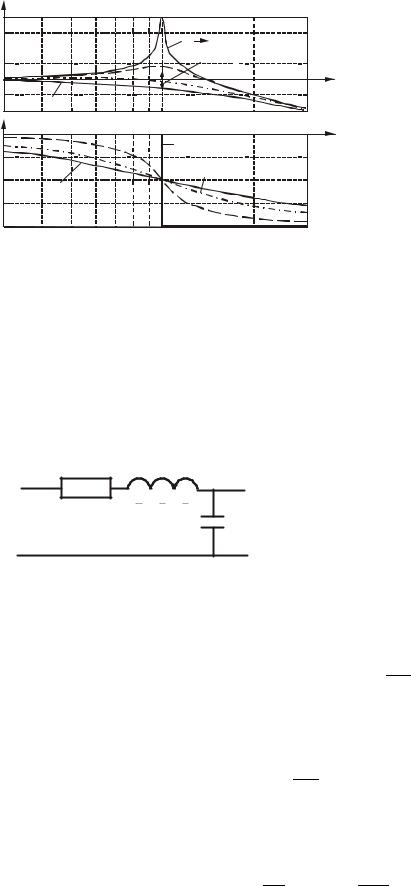
скачкообразное изменение фазы от 0 до 180° . Графики ЛАЧХ и ЛФЧХ показаны на рис.2.52.
67
Lm(ω) |
|
|
|
|
|
ξ |
0 |
|
|
|
−6 дБ |
|
|
|
lg(ω) |
|
ξ=1 |
ωс=1/T |
ω |
|
|
||
ϕ(ω) |
|
|
lg(ω) |
0 |
|
ξ= 0 |
ω |
|
|
||
−π/2 |
|
0<ξ<1 |
|
ξ=1 |
|
||
|
|
||
−π |
|
|
|
Рис.2.52. Графики ЛАЧХ и ЛФЧХ колебательного |
|||
звена при различных значенияx относительного |
|||
|
|
коэффициента затухания ξ |
|
Колебательные звенья способны накапливать два вида энергии: кинетическую и потенциальную. Процесс колебаний сопровождается переходом одной энергии в
другую, и наоборот. Примерами колебательного звена могут служить:
∙металлический демпфер;
∙акселерометр (измеритель ускорения);
∙RLC-контур в радиотехнике (рис.2.53).
|
R |
L |
|
|
U1 |
|
C |
U2 |
|
Рис.2.53. RLC-контур - пример |
|
|||
реализации колебательного звена |
|
|||
Входным сигналом RLC-контура является напряжение U1 , выходной величиной - |
||||
напряжение на конденсаторе U 2 |
. Если цепь не нагружена и ток в цепи i(t) = C du2 |
, то в |
||
|
|
|
dt |
|
соответствии с законом Кирхгофа уравнение динамики контура:
U1 |
= Ri(t) + L |
di(t) |
+ U 2 . |
|
dt |
||||
|
|
|
После несложных преобразований с учетом того, что i(t) = C dudt2 , получим:
é |
du |
2 |
ù |
|
d é |
du |
2 |
ù |
|
|
|
RêC |
|
ú |
+ L |
|
êC |
|
ú |
+ U2 |
= U1; |
||
dt |
|
dt |
|||||||||
ë |
û |
|
dt ë |
û |
|
|
|||||
LC |
d 2u |
+ RC |
du |
+ U2 |
= U1. |
|
dt 2 |
dt |
|||||
|
|
|
|
Последнее уравнение после введения обозначений T = 
 LC ; x = 0,5R
LC ; x = 0,5R
 C / L приводится к стандартному виду:
C / L приводится к стандартному виду:
68
