31.Явления в нелинейных цепях переменного тока.

32.Методы расчета нелинейных цепей переменного тока. Графический расчёт с использованием характеристик для мгновенных значений

       В качестве примера  использования характеристик для мгновенных значений построим при синусоидальной ЭДС кривую тока в цепи на рисунке 16.1, для которой ВАХ диода представлена на рисунке 16.2.

Рисунок16.1Рисунок 16.2

 

       1. Строим результирующую ВАХ u(i)цепи ( рисунок 16.2) согласно соотношению .Находя для различных значений e(t)с использованием полученной кривой соответствующие им значения тока, строим по точкам (рисунок 16.3) кривую искомой зависимостиi(t) .Важнейшим элементом в цепях переменного тока является катушка с ферромагнитным сердечником. В общем случае кривая зависимости ψ(i)имеет вид гистерезисной петли, но, поскольку в устройствах, работающих при переменном напряжении, используются магнитные материалы с узкой петлей гистерезиса, в большинстве практических случаев допустимо при расчетах использовать основную кривую намагничивания. Условное изображение нелинейной катушки индуктивности приведено на рисунке 16.4.

Здесь Ф–основной поток, замыкающийся по сердечнику,Фs- поток рассеяния, которому в первом приближении можно поставить в соответствие потокосцепление рассеяния,ψs=LsI где индуктивность рассеянияLs=constв силу прохождения потоком части пути по воздуху. Так как характеристика ψ(i)катушки симметрична относительно начала координат, а напряжениеU(t)симметрично относительно оси абсцисс (оси времени), то кривая ψ(t)также должна быть симметричной относительно последней. Находя для различных значенийψ(t)с использованием кривой ψ(i)соответствующие им значения тока, строим по точкам ( рисунок 16.5) кривую зависимостиi(t) .

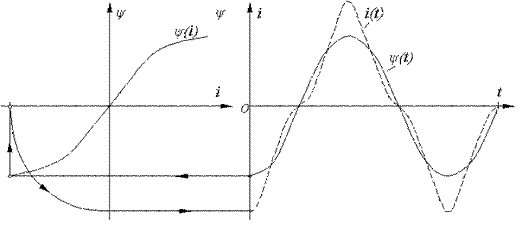Рисунок 16.

2)Метод эквивалентных синусоид.При анализе нелинейной цепи данным методом реальные несинусоидально изменяющиеся переменные заменяются эквивалентными им синусоидальными величинами, действующие значения которых равны действующим значениям исходных несинусоидальных переменных. Кроме того, активная мощность, определяемая с помощью эквивалентных синусоидальных величин, должна быть равна активной мощности в цепи с несинусоидальной формой переменных. Переход к эквивалентным синусоидам позволяет использовать при анализе цепей векторные диаграммы.Рассмотрим данный метод на примере исследования явлений в цепях, содержащих нелинейную катушку индуктивности и линейный конденсатор (феррорезонансных цепях). Различают феррорезонанс в последовательной цепи (феррорезонанс напряжений) и феррорезонанс в параллельной цепи (феррорезонанс токов). Рассмотрим первый из них на основе схемы на  рисунке 16.6. Для этого строим  (рисунок 16.7) прямую зависимостиUc(I).Далее для двух значений сопротивлений R (R=0иR≠0) строим графики зависимостей U(I):для R=0-согласно соотношению U(I)=UL(I)-Uc(I)(кривая на рисунке 16.7); дляR≠0-согласно выражению

Рисунок 16.6          Рисунок 16.7

(кривая на рисунке 16.7). Точка пересечения кривойUL(I)с прямой Uc(I)соответствует феррорезонансу напряжений. Феррорезонансом напряжений называется такой режим работы цепи, содержащей последовательно соединенные нелинейную катушку индуктивности и конденсатор, при котором первая гармоника тока в цепи совпадает по фазе с синусоидальным питающим напряжением.