61. Уравнения Максвелла

1.Основные понятия

Основные законы электродинамики (уравнения Максвелла) были сформулированы в 1873 году. По своей значимости они аналогичны законам Ньютона в механике. Современная формулировка дана Герцем и Хевисайдом. Эти уравнения связывают характеристики электромагнитного поля и его источники.

В данные уравнения входят - напряженность электрического поля, индукция магнитного поля. Эти величины являются основными, т.к. определяют силу, действующую на заряженную частицу (Fл) – силу Лоренца.

Входят две вспомогательные величины - индукция электрического поля и - напряженность магнитного поля. Также входят - плотность тока и ρ - плотность заряда.

Уравнения Максвелла позволяют по известному полю найти токи и заряды (достаточно просто), а также по известным токам и зарядам найти поле (сложно).

2.Интегральная форма

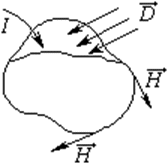
I уравнение представляет собой обобщение закона полного тока.

Закон: Циркуляция напряженности магнитного поля по произвольному замкнутому контуру определяется током проводимости и быстротой изменения потока электрической индукции через произвольную поверхность, охваченную данным контуром.

II уравнение обобщает закон электромагнитной индукции.

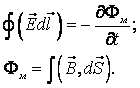
Закон: Циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения потока магнитной индукции через площадку, охваченную данным контуром, взятой с обратным знаком

III уравнение: теорема Гаусса для электрической индукции.

Закон: Поток электрической индукции через произвольную замкнутую поверхность определяется зарядом внутри этой поверхности.

IV уравнение: закон Гаусса для индукции магнитного поля.

Закон: Поток индукции магнитного поля через произвольную замкнутую поверхность равен нулю.

3.Дифференциальная форма

Используя формулы Остроградского-Гаусса и Стокса можно получить

I уравнение Максвелла.

II уравнение Максвелла.

III уравнение Максвелла.

IV уравнение Максвелла

4.Материальные уравнения

В систему уравнений Максвелла входят 16 скалярных функций координат и времени. Самих уравнений – 8.

Чтобы замкнуть эту систему, используют материальные уравнения.

Величины e, μ, σ получаются из других разделов физики или определяются экспериментально.

62.Теорема Умова-Пойнтинга.

(ВОПРОСНИОЧЕМ)

Для теории электромагнитных полей важное значение имеет формулировка законов сохранения энергии и импульса. Мы начнем с рассмотрения закона сохранения энергии, который часто называют теоремой Пойнтинга (1884 г.). Работа, совершаемая электромагнитным полем Е, В в единицу времени над отдельным зарядом q, равна где v — скорость заряда. Магнитное поле работы не совершает, поскольку магнитная сйла перпендикулярна скорости. При непрерывном распределении зарядов и токов полная работа, совершаемая полем в объеме V в единицу времени., равна

Это выражение определяет скорость превращения электромагнитной энергии в механическую или тепловую. Очевидно, с такой же скоростью уменьшается энергия электромагнитного полявнутри объема V. Чтобы найти этот закон сохранения в явном виде, преобразуем выражение с помощью уравнений Максвелла. Для исключения J воспользуемся законом Ампера — Максвелла:

Учитывая векторное тождество

и закон Фарадея, преобразуем правую часть (6.78) к виду

Для дальнейшего необходимо сделать два допущения. Первое из них не имеет существенного значения и делается только для простоты. Будем предполагать, что макроскопическая среда обладает линейными электрическими и магнитными свойствами. Тогда два члена в, содержащие производные по времени, можно в соответствии с и интерпретировать как производные по времени от плотностей электростатической и магнитной энергий. Теперь мы сделаем второе предположение, а именно будем считать, что сумма выражений и представляет собой полную электромагнитную энергию также и в случае переменных во времени полей. Если плотность полной энергии поля обозначить через

то перепишется в виде

Поскольку объем V произволен, это соотношение можно представить в форме дифференциального закона сохранения, или уравнения непрерывности:

Вектор S, определяющий поток энергии, называется вектором Пойнтинга. Он равен

и имеет размерность энергия/(площадь X время). Так как в законе сохранения фигурирует только дивергенция этого вектора, к вектору Пойнтинга можно прибавить ротор произвольного вектора поля. Однако этот добавочный член не приводит ни к каким физическимследствиям, и поэтому обычно используется частная форма.

Физический смысл интегральной или дифференциальной формы законов или заключается в том, что скорость возрастания электромагнитной энергии внутри некоторого объема в сумме с энергией, вытекающей за единицу времени через поверхность, ограничивающую этот объем, равна взятой со знаком минус полной работе, совершаемой полем над источниками внутри данного объема. Соотношения выражают закон сохранения энергии. Если имеются нелинейные эффекты, такие, как гистерезис в ферромагнитных материалах, то простая форма закона сохранения неприменима и необходимо добавить соответствующие члены, учитывающие потери на гистерезис.