1.Четырехполюсники и их основные уравнения.

Четырехполюсником называется часть электрической цепи или схемы, содержащая два входных вывода (полюса) для подключения источника энергии и два выходных вывода для подключения нагрузки. К четырехполюсникам можно отнести различные по назначению технические устройства: двухпроводную линию, двухобмоточный трансформатор, фильтры частот, усилители сигналов и др.

Если четырехполюсник не содержит внутри себя источников энергии, то он называется пассивным (обозначается буквой П), если внутри четырехполюсника имеются источники, то он называется активным (обозначается буквой А).

На электрических схемах четырехполюсники условно обозначаются прямоугольником с двумя парами выводов: 1 и 1' - входные выводы, 2 и 2' - выходные выводы (рис. 75.1). Соответственно напряжение и ток на входе индексируются цифрой 1 (U1, I1) , а на выходе - цифрой 2 (U2, I2).

Для записи уравнений четырехполюсника выделим в произвольной схеме ветвь с единственным источником энергии и любую другую ветвь с некоторым сопротивлением   (см. рис. 1,а).

В соответствии с принципом компенсации заменим исходное сопротивление   источником с напряжением   (см. рис. 1,б). Тогда на основании метода наложения для цепи на рис. 1,б можно записать

;

(1)

 

.

(2)

Решая полученные уравнения (1) и (2) относительно напряжения и тока на первичных зажимах, получим

;

или

;

(3)

,

(4)

где  ;  ;  ;   - коэффициенты четырехполюсника.

Учитывая, что в соответствии с принципом взаимности  , видно, что коэффициенты четырехполюсника связаны между собой соотношением

.

(5)

Уравнения (3) и (4) представляют собой основные уравнения четырехполюсника; их также называют уравнениями четырехполюсника в А-форме (см. табл. 1). Вообще говоря, существует шесть форм записи уравнений пассивного четырехполюсника. Действительно, четырехполюсник характеризуется двумя напряжениями   и   и двумя токами    и  . Любые две величины можно выразить через остальные. Так как число сочетаний из четырех по два равно шести, то и возможно шесть форм записи уравнений пассивного четырехполюсника, которые приведены в табл. 1. Положительные направления токов для различных форм записи уравнений приведены на рис. 2. Отметим, что выбор той или иной формы уравнений определяется областью и типом решаемой задачи.

 

Таблица 1.    Формы записи уравнений пассивного четырехполюсника

Если при перемене местами источника и приемника энергии их токи не меняются, то такой четырехполюсник называется симметричным. Как видно из сравнения А- и В- форм в табл. 1, это выполняется при  .

Четырехполюсники, не удовлетворяющие данному условию, называются несимметричными.

2.Определение коэффициентов четырехполюсника.

Коэф 4хполюсника зависят от конфигурации и параметров элементов схемы 4полюсника и для данного 4хполюсника яв-ся пост величиной.

Коэф 4хполюсника можно найти расчетным путем, если заданы схема и параметры эл-ов или опытным путем измеряем напряж и токи

Прежде всего, коэф определяются из режимов холостого хода и короткого замыкания

Сущность первого метода состоит в том, что сложная схема четырехполюсника путем последовательных преобразований сворачивается к простейшей Т- или П-образной схеме. Коэффициенты четырехполюсника определяются по соответствующим формулам, полученным ранее для этих схем.

    Пусть требуется определить коэффициенты четырехполюсника, схема которого приведена на рис. 77.1.

    Выполняется первое преобразование: треугольник Z₂, Z₃, Z₄ преобразуется в эквивалентную звезду Z₆, Z₇, Z₈ (рис. 77.2):

    Затем выполняются последовательные преобразования Z_1э=Z1+Z6, Z_2э=Z7+Z5, Y0=1/Z8, после чего схема получает стандартный Т-образный вид (рис. 77.3):

    Коэффициенты четырехполюсника находятся по формулам для Т-схемы:

    Сущность второго метода заключается в том, что коэффициенты четырехполюсника определяются через его входные сопротивления со стороны входных (Z_1X и Z_1K) и выходных (Z_2X и Z_2K) выводов в режимах холостого хода и короткого замыкания на противоположной стороне. Значения этих сопротивлений рассчитываются аналитически методом свертки схемы четырехполюсника в соответствующем режиме (х.х. или к.з.) относительно его выводов.

    При питании четырехполюсника со стороны первичных выводов применяются уравнения формы А:

    В режиме холостого хода на вторичной стороне I_2X = 0, а в режиме короткого замыкания U_2K = 0. Из уравнений следует:

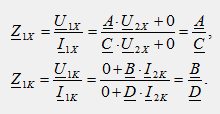
    При питании четырехполюсника со стороны вторичных выводов применяются уравнения формы В:

    В режиме холостого хода на первичной стороне I_1X = 0, а в режиме короткого замыкания - U_1K = 0. Из уравнений следует:

    Совместное решение полученных уравнений позволяет установить связь между входными сопротивлениями четырехполюсника в режиме холостого хода и короткого замыкания, но не дает возможности определить его коэффициенты:

    Для определения коэффициентов четырехполюсника берут любые три из четырех уравнений для входных сопротивлений и дополняют их уравнением связи между коэффициентами AD-BC = 1, после чего решают полученную систему из четырех уравнений. В качестве примера возьмем уравнения для Z_1X, Z_2X и Z_2K, тогда получим:

    Из уравнений (1), (2) и (3) делаем подстановку в уравнение (4), получим:

    Остальные коэффициенты (B, C, D) получим путем подстановки найден¬ного значения А в уравнения (1), (2) и (3).