Билеты с ответами / 17

17 билет

1. В основе метода лежит принцип суперпозиции (наложения): ток в любой ветви сложной электрической цепи, содержащей несколько ЭДС, может быть найден как алгебраическая сумма токов в этой ветви от действия каждой ЭДС в отдельности.

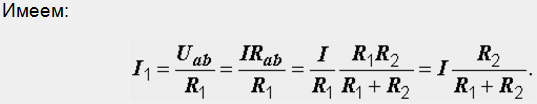
Из полученной формулы вытекает правило: ток в одной из двух параллельных ветвей равен произведению общего тока на сопротивление соседней ветви, деленному на сумму сопротивлений параллельных ветвей.

Или

Метод наложения

Метод наложения целесообразно использовать в тех случаях, когда нужно рассчитать ток в одной из ветвей в разветвленной цепи, при этом производится расчет частичных токов создаваемых в этой ветви каждым из источников в отдельности, затем действующий ток в этой ветви находится как алгебраическая сумма частичных токов, т.е с учетом их сопротивлений.

12.Входные и взаимные проводимости ветвей

По принципу наложения ток в любой ветви (к) можно представить как алгебраическая сумма частичных токов от (n) источников. 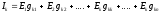Проводимость с двумя одинаковыми индексами называется входной проводимостью данной ветви. Она численно равна отношению частичного тока создаваемого в этой ветви источником, включенным в эту же ветвь и ЭДС этого источника.

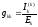
Проводимость с двумя разными индексами называется взаимной проводимостью двух ветвей. Взаимная проводимость 2х ветвей численно равна отношению частичного тока создаваемого в одной ветви с источником ЭДС включенным в другую ветвь к величине ЭДС этого источника. 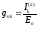. Входные и взаимные проводимости зависят от конфигурации схемы и от величины сопротивления и для данной схемы являются неизменными характеристиками ; .

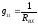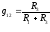2. цепей со смешанным соед-м компл. сопротивлений Расчёт цепей со смешанным соед компл токов

 .
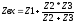