
Билеты с ответами / XXXTOE_33_33_33
.doc1.Осн.понятия синус-го тока
Синус-й ток
–изменяющ-я ток во времени по синусиод-му
закону.Мгно-ое знач-ие синус-го тока
запис-я в след. виде «i».![]()
![]() -начал-я
фаза.
-начал-я
фаза.
2.Действую-ее значение син-го тока
Действ-ее знач-е
син-го тока это среднеквадратичное
знач-е за период, запис-я:
 .Дейст-ее
знач-ее перемен-го тока численно равно
такому постоян-му току,который за
интервал времени равный периоду
переменного тока,выделяет такое кол-во
тока,что и перем-й ток.Выведем выражение
действ-ее знач-е син-го тока через его
амплитуду:
.Дейст-ее
знач-ее перемен-го тока численно равно
такому постоян-му току,который за
интервал времени равный периоду
переменного тока,выделяет такое кол-во
тока,что и перем-й ток.Выведем выражение
действ-ее знач-е син-го тока через его
амплитуду: ,
, ,
,
 .
.
3.Изображение син- величин времени,векторами и комклекс-ми числами
![]()
На комплек-й пл-ти
построим вектор длина которого в
выбранном масштабе равна амплитуде
син-го тока, а угол наклона относ-но
действ-й оси равен нач-й фазе
![]() .
.
Придадим данному
вектору вращение с угловой скоростью
равной угловой скорости
![]() в
направлении против часовой стрелки.
в
направлении против часовой стрелки.
Через промежуток
времени t
вектор повернется на угол
![]() .
.
Возьмем проекцию
этого вектора на ось мнимых чисел:
![]()
Таким образом,
проекция вращающегося вектора
![]() на
ось мнимых чисел в любой момент времени
соответствует мгновенному знач-ю тока,
поэтому вращя-ся вектор явл-я изображением
син-го тока.
на
ось мнимых чисел в любой момент времени
соответствует мгновенному знач-ю тока,
поэтому вращя-ся вектор явл-я изображением
син-го тока.
Для изображения
син-го тока достаточно брать выражение
вращя-ося вектора при t
равного нулю:
![]()
Эта величина наз-я
компл-ой амплитудой и обоз-я
![]() .
.
![]() Можно
записать комплексно дейст-ее значение:
Можно
записать комплексно дейст-ее значение:
 .
.
![]()
Таким образом, любую син-ю величину можно представлять в виде вектора на комплексной пл-ти или комплексного числа.
![]()

![]() - комплекс напряжения
на индуктивности.Умножение на j
соответствует повороту вектора в сторону
опережения на угол пи пополам.
- комплекс напряжения
на индуктивности.Умножение на j
соответствует повороту вектора в сторону
опережения на угол пи пополам.
 - комплексное
напряжение на конденсаторе.При переходе
к комплексам, производные и интегралы
заменяются прост алегбр выр-ми.вследствие
чего диффер ур-е отн-но мгн значений
заменяются алгебр ур-ми для комплексов
напряжений и токов.
- комплексное
напряжение на конденсаторе.При переходе
к комплексам, производные и интегралы
заменяются прост алегбр выр-ми.вследствие
чего диффер ур-е отн-но мгн значений
заменяются алгебр ур-ми для комплексов
напряжений и токов.
6.Закон Ома в компл форме для послед цепи RLC:
х

Каждый из комплексов представим в показ форме , тогда закон ома для действ значений будет записан (так же тока без точек)
7.Векторная диаграмма для посл цепей RLC
В.Д.- сов-ть векторов изображающих напряжение и токи нанесенных на комплексную плоскость.
Для построения выбираем вектор тока:
1)тогда откладываем против часовой стрелки угол фи от положит полуоси действ чисел
2)отн-но тока строим вектора напряжения, для этого выбир масштаб напряжения. Вектор Ur откладываем по направлению тока
3)из конца вектора Ur строим вектор напр-я на индуктивности с учетом, что напр-е на инд-ти опережает вектор тока на пи пополам.
4)из конца Ul строим вектор напр-я на емкости учитывая Uc отстает от тока на 90
8.Сопротивление в цепях синусоидального тока
В цепи синусоидального тока использ нес-ко видов сопротивлений.
Комплексное сопротивление Z

R-активное сопрот-е
X-реактивное сопр-е
XL=wL
Xc=![]()
Таким образом,реактив сопр-е цепи опр как разность реак сопр инд-ти и емкостей и емкостей.Реак сопр-е инд-ти и емкости

9.Разность фаз напряжения и тока
Угол сдвига фаз
между рапряжением и тока
![]() равен разности начальных фаз напряжения
и тока
равен разности начальных фаз напряжения
и тока
![]()
![]() -определ-я
характером комплексного соед-я
-определ-я
характером комплексного соед-я
![]() -
реакт-е сопр-е цепи.
-
реакт-е сопр-е цепи.
Если
![]() ,то
характер цепи акт.-индук-й
и
,то
характер цепи акт.-индук-й
и
![]() .Напряжение
опережает по фазе ток.
.Напряжение
опережает по фазе ток.
![]() - акт.-инд-й
- акт.-инд-й
Характер цепи акт.-емкостный
![]()
![]() -
акт.-емкост-й
-
акт.-емкост-й
Угол сдвига фаз
изменяется в пределах
![]() при чисто емкостном сопрот-и
при чисто емкостном сопрот-и
При
![]() (резонанс).
(резонанс).
10. Параллельное соединение R,L,C


Ток через акт.сопр-е
совпадает по фазе с напряжением, ток
ч/з индук-ть отстает, а ток ч/з емко-ть
опережает на угол
![]() по фазе напряжения
по фазе напряжения
Ток на входе по I зак-у Кирхгофа равен сумме токов

-Закон Ома для парал-го RLC
11. Проводимости в цепях син-го тока
Компле-ая проводимоть
в цепиУ равна отношению компл. Тока к
компл-му U
 у-полная
проводимость в цепи равная модулю
проводимости
g=
у-полная
проводимость в цепи равная модулю
проводимости
g=![]() b=
b=![]() для
паралл. Цепи rlc
для
паралл. Цепи rlc

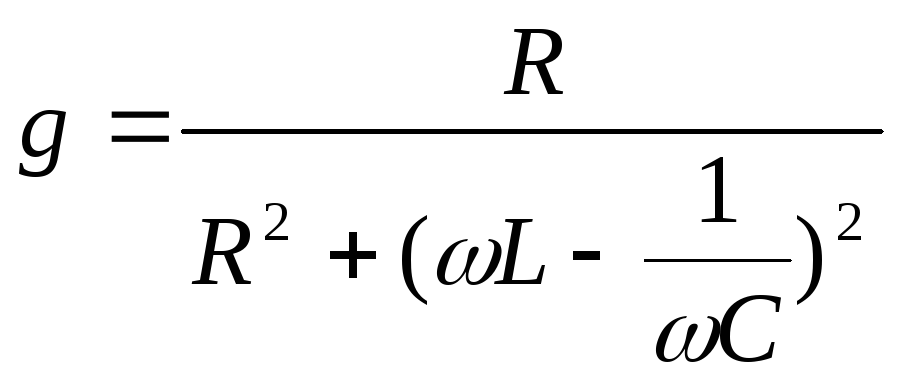
 а
общем случае акт проводимость зависит
ещё и от реактивн. Проводимости и
наоборот
12.Законы
Кирхг. В комплексной форме
1
з-н.Сумма
компл токов сходящ в узле равна 0. -
а
общем случае акт проводимость зависит
ещё и от реактивн. Проводимости и
наоборот
12.Законы
Кирхг. В комплексной форме
1
з-н.Сумма
компл токов сходящ в узле равна 0. -
![]() 2
з-н.в замкн
контуре алг сумма произведений компл
токов на компл. Сопрот-я ветвей равна
алг. Сумме компл. ЭДС
2
з-н.в замкн
контуре алг сумма произведений компл
токов на компл. Сопрот-я ветвей равна
алг. Сумме компл. ЭДС
![]() 13.
Расчёт цепей синусоид-го тока в компл.
Форме.Расчёт цепей с послед соед-м компл.
Сопротивлений.
13.
Расчёт цепей синусоид-го тока в компл.
Форме.Расчёт цепей с послед соед-м компл.
Сопротивлений.
 14.
Расчёт цепей со смешанным соед-м компл.
сопротивлений
Расчёт
цепей со смешанным соед компл токов
14.
Расчёт цепей со смешанным соед-м компл.
сопротивлений
Расчёт
цепей со смешанным соед компл токов
![]() 15.
Расчёт разветвл. цепей синусоид тока
комплл мет-м
При
к расчёте цепей синусоид тока в компл.
Ф. могут исп-ся все изв. М-ды расчёта
разветвл. Цепей.
15.
Расчёт разветвл. цепей синусоид тока
комплл мет-м
При
к расчёте цепей синусоид тока в компл.
Ф. могут исп-ся все изв. М-ды расчёта
разветвл. Цепей.

 16.
Топографи-я
диаграмма
Топограф.
Диаграмма представл собой совокупн
комплексных потенциалов точек цепи
нанесённых на компл пл-сть
Для построения
топографич диагр потенциал 1-й из точки
принимаем за 0
Рассчитыв-ся компл.
Потенциалы всех точек цепи затем они
наносЯтся на компл пл-сть
16.
Топографи-я
диаграмма
Топограф.
Диаграмма представл собой совокупн
комплексных потенциалов точек цепи
нанесённых на компл пл-сть
Для построения
топографич диагр потенциал 1-й из точки
принимаем за 0
Рассчитыв-ся компл.
Потенциалы всех точек цепи затем они
наносЯтся на компл пл-сть
![]() Точки на компл плсти соедин-ся отрезками
прямых в соответсвии со схемойком при
смешан
Рассм качеств построение
топографич диагр с 1 источн при смеш
соединении
Точки на компл плсти соедин-ся отрезками
прямых в соответсвии со схемойком при
смешан
Рассм качеств построение
топографич диагр с 1 источн при смеш
соединении
Затем соед-ем
N
с O
получаем точку пересечения с дугой
окружн-ти М
В масштабе напря-й отрезок
ОМ изобр-т напряжение на неизмен-м
сопро-и Z1
отрезок МК изобр-т напряжение на пременном
U2
Пассивный
2-хполюсник в цепи синусоид тока. Содерж
только потр.
![]()
![]() пассивн
2хполюсн можно заменить экв схемой с
послед соед-м реакт и акт сопротивл.
пассивн
2хполюсн можно заменить экв схемой с
послед соед-м реакт и акт сопротивл.
18.
Мощности в цепях син-го тока
Мгновен-я
мощность - р=ui
Акт-я
мощность представляет собой среднее
значение за период:
![]() Акт-я мощ-ть
харак-т процесс преобразования электр-й
энергии в другии виды энергии
Акт-я мощ-ть
харак-т процесс преобразования электр-й
энергии в другии виды энергии
Реакт-я мощ-ть:
![]()
![]()
Реак-я мощ-ть харк-т запас электромаг-й энергии создаваемой в электрич-х полях емкости и магн-х полях индук-ти
Полная мощ-ть S
![]() S=UI
коэф-ты мощ-ти:
S=UI
коэф-ты мощ-ти:
Cosy=P/S , tgy=Q/P
![]()
Все три вида мощ-ти можно объед-ть с помощью компл-й мощ-ти.
![]() равна произ-ю
равна произ-ю
![]() на сопря-й комплекс тока
на сопря-й комплекс тока
![]() ----
----![]()
![]()
19. Мощности сопротивлений индук-ти
Q=0
P=S=UI
Таким образом, акт.сопрот-е явл-я потребит-м только активной мощности.
![]()
P=0, Q=S=UI
Таким образом, инд-ть явл-ся потре-м только реакт-й мощ-ти, потреб-я акт-я мощ-ть равна нулю.
![]()
P=0, Q=-UI
Таким образом, емкость явл-я генератором реакт-й мощ-ти.Реакт-я мощ-ть цепи опр-я как разность
![]()
20. Баланс мощ-ти в цепях син-го тока
Для полных мощ-й баланс не состав-я,можно составлять только для акт-х и реакт-х мощ-й.
Ур-е баланса для комл-х мощ-й:
![]()
![]() ,
,
![]()
Из баланса компл-х мощ-й следует баланс для акт-х и реакт-х мощн-й
![]()
 Резонансовое
явл-е в электрич-х цепях
Резонансовое
явл-е в электрич-х цепях
Фазовый резонанс в эл-й цепи наблюдается при условии, что напряж и ток на входе цепи совпадают по фазе. Это возможно при усл-ии, что вход-е реак.сопрот-е или вход-е реак-я проводимость равна нулю.
Резонанс напряжений
Резонанс напр-ий набл-я в последней цепи содержащей катушки индук-и и емкости.

X=0;
![]()
![]()
Добиться резонанса
можно изменяя одну из трех величин:
частоты, индуктивности, емкости. Резонанс
частота
![]() получается из равенства.
получается из равенства.
![]() .
.
Добротность
цепи это отн-ие напр-ия на индуктивность
или емкости в режиме резонанса к входному
напряжению.
![]()
![]()
![]()
![]() =IR
=IR
![]() Q-называют
коэф-м резонанса т к она показывает во
ск-ко раз U
индуктивности или Uёмкости
превышает напряж на входе
Частотные
хар-ки послед цепи RLC
Q-называют
коэф-м резонанса т к она показывает во
ск-ко раз U
индуктивности или Uёмкости
превышает напряж на входе
Частотные
хар-ки послед цепи RLC
![]()
![]()
![]() Построим
зависимости
Построим
зависимости
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() При
увеличении от
При
увеличении от
![]() скор
возрастания сопрот-я инд-сти больше чем
поэтому напряжение на инд-сти
OL
продолжает расти.
скор
возрастания сопрот-я инд-сти больше чем
поэтому напряжение на инд-сти
OL
продолжает расти.
![]()
![]()
![]()
![]() Резонансные
кривые при изменении параметров
Резонансные
кривые при изменении параметров
![]()
![]()
![]() L=const
I=0
L=const
I=0
![]()
![]()
![]()
![]()
![]()
Резонанс токов
Наблюдается в параллельной цепи.в одной в одной катушке L в другой емкость С
Резонанс наступает при условии, что вх реакт пров-ть =0 (b=0)
b=0;![]()
![]() ;
;
![]() -
-

Резонансная частота имеет действ значение при условии
![]() или
или
![]()
![]() При
резонансе ток меньше чем токи парал
ветвей. В идеале:
При
резонансе ток меньше чем токи парал
ветвей. В идеале:
![]()
Цепи cо взаимными инд-тью.индукционно связан эл-ты цепи.
Два эл-та наз инд-но связанными если при пропуск тока по одному из нихна зажимах второго возник ЭДС и наоборот.
Пропустим ток по
первой катушке. Этот ток создаст
магнит.поток самоиндукции
![]() связанный с 1-й катушкой и магнит поток
взаимоиндукции
связанный с 1-й катушкой и магнит поток
взаимоиндукции
![]() связан
со 2-й катушкой.
связан
со 2-й катушкой.
Инд-ть 1й катушки
равна
![]()
Взаим инд-ть м/у катушками
![]()
Пропустим ток
![]() по
2 й катушке.он создаст магн поток
самоиндукции
по
2 й катушке.он создаст магн поток
самоиндукции
![]() связан
со 2й катушкой и поток взаим индукции
связан
со 2й катушкой и поток взаим индукции
![]() связан с 1 катушкой
связан с 1 катушкой![]()
![]()
![]()
Степень инд-й двух катушек хар-ся коэф-том инд-й связи К
![]()
![]()
![]() ,
,![]() след-но
след-но
![]()
Магнит поток взаим
инд меньше магнит потоков самоинд,поэтому
![]()
ЭДС и напряжение взаим индукции
Для определения знака напряж и ЭДС необх разметка зажимов двух инд-но связан катушек.
Два зажима пренадлеж двум разным катушкам наз одноимен если при одинок направлениях токов отн-но одноименных зажимов 2х катушек. Магнит потоки само и взаим инд –ии имеют одинак напр-е………………………………
