- •Биофизическая химия Сборник примеров и задач
- •Оглавление
- •Введение
- •1. Термодинамическое описание биохимических реакций
- •1.1. Расчёт изменения свободной энергии химических реакций
- •1.2. Практические расчёты при описании биохимических реакций
- •Примеры решения задач
- •Теоретические вопросы для самоподготовки
- •2. Стехиометрические расчёты биотехнологических процессов
- •2.1. Стехиометрия и материальный баланс микробиологических процессов
- •2.2. Расчёт выхода биомассы на субстрат (источник углерода)
- •Значения γs и максимальные теоретические значения выхода биомассы для различных субстратов
- •Оценка теплового эффекта и свободной энергии некоторых процессов биосинтеза
- •Задачи для самостоятельного решения
- •Данные для решения задачи 1
- •Данные для решения задачи 2
- •Теоретические вопросы для самоподготовки
- •3. Ферментативная кинетика и катализ
- •3.1. Общая характеристика ферментов
- •3.2. Кинетическое описание ферментативных процессов
- •3.3. Различные типы координат, используемые для графического решения уравнения Михаэлиса–Ментен
- •3.4. Интегральная форма уравнения Михаэлиса–Ментен
- •3.5. Ингибирование ферментативных реакций
- •Кинетические схемы, основные формулы различных ферментативных процессов
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Теоретические вопросы для самоподготовки
- •Заключение
- •Приложение 1
- •Приложение 2 Константы диссоциации аминокислот, органических кислот и оснований
- •Константы диссоциации различных соединений при 25 °с
- •Приложение 3 Элементарный состав сухой биомассы микроорганизмов
- •Элементарный состав сухой биомассы микроорганизмов
- •Элементарный состав и восстановленность сухой биомассы микроорганизмов, выращенных в условиях непрерывного культивирования
- •Элементный состав и восстановленность сухой биомассы микроорганизмов различных типов дрожжей, выращенных в условиях непрерывного культивирования при лимитировании роста субстратом
- •Список литературы
- •Суясов Николай Александрович
3.4. Интегральная форма уравнения Михаэлиса–Ментен
Значительным недостатком классической исходной формы уравнения Михаэлиса–Ментен (3.10) является необходимость сбора огромного массива экспериментальных данных для определения кинетических характеристик ферментативных процессов. Альтернативой, позволяющей определить кинетические характеристики ферментативной реакций при минимальном количестве экспериментов, является интегральная форма уравнения Михаэлиса–Ментен. Исходное дифференциальное уравнение Михаэлиса–Ментен может быть представлено следующим образом:
![]() ;
;
![]() ;
;
![]() .
.
Проведём интегрирование уравнения:
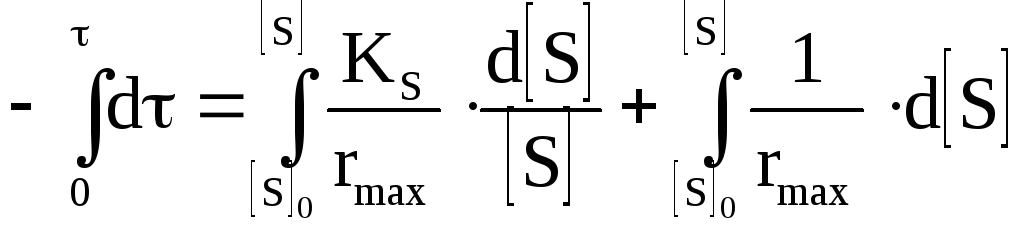 ;
;
![]() ;
;
![]() .
(3.14)
.
(3.14)
Уравнение (3.14) представляет собой интегральную форму уравнения Михаэлиса–Ментен. После преобразования получим:
![]() .
(3.15)
.
(3.15)
Линейные преобразования (3.15) графически представляются прямой с углом наклона |tgα| = KS (рис. 3.6).

Рис. 3.6. Линеаризация зависимости, описываемой интегральной формой уравнения Михаэлиса–Ментен (3.14)
3.5. Ингибирование ферментативных реакций
Скорость ферментативных реакций может быть частично снижена или полностью заблокирована определёнными соединениями. Вещества, подавляющие каталитическую активность ферментов, называют ингибиторами. Также активность многих ферментов тормозится избытком субстрата.
Ингибитор способен к образованию комплекса с ферментом, но не может быть подвергнут каталитическому превращению и препятствует образованию комплекса фермент-субстрат. Инактивация фермента предполагает либо необратимое связывание фермента с отравляющими фермент веществами, либо разрушение структуры фермента под действием физико-химических параметров. В отличие от обратимого ингибирования, при инактивации активность фермента уменьшается во времени.
Исследование подавления активности ферментов служит одним из способов изучения специфичности действия ферментов и расшифровки механизма их действия.
Основные типы ингибирования, а также ряд других типичных для ферментативных реакций процессов, представлены в табл. 3.1.
Таблица 3.1
Кинетические схемы, основные формулы различных ферментативных процессов
|
Кинетическая схема |
Основные формулы |
Графическое решение |
|
Однокомпонентное полностью конкурентное ингибирование фермента | ||
|
|
|
Рис. 3.7а, б
Анализ
в координатах Диксона
рис.
3.7 (в) |
|
Однокомпонентное полностью неконкурентное ингибирование фермента | ||
|
|
|
Рис. 3.8.(а, б)
Анализ
в координатах Диксона
рис. 3.8 (в) |
|
Продолжение табл. 3.1 | ||
|
Двухкомпонентное взаимозависимое полностью конкурентное ингибирование фермента | ||
|
|
|
Рис. 3.9 |
|
Двухкомпонентное взаимонезависимое полностью конкурентное ингибирование фермента | ||
|
|
|
|
|
Продолжение табл. 3.1 | ||
|
Двухкомпонентное взаимонезависимое полностью неконкурентное ингибирование фермента | ||
|
|
|
Рис. 3.10 |
|
Ингибирование фермента высокими концентрациями субстрата | ||
|
|
ES2
– неактивный комплекс
Если
высокие концентрации [S]:
|
Рис. 3.11 (а, б) |
|
Продолжение табл. 3.1 | ||
|
Ингибирование фермента продуктом по полностью конкурентному типу | ||
|
|
|
Рис. 3.12 |
|
Обратимая изомеризация фермента в неактивную форму | ||
|
|
[S] высокая:
[S] низкая:
|
|
|
Продолжение табл. 3.1 | ||
|
Необратимая инактивация фермента в свободном виде | ||
|
|
k ин – константа скорости
|
Рис. 3.13 |
|
Необратимая инактивация фермента в составе фермент-субстратного комплекса | ||
|
|
|
Рис. 3.14 |
|
Окончание табл. 3.1 | ||
|
Влияние кислотности среды на кинетику ферментных реакций | ||
|
|
|
Рис. 3.15, 3.16 |
|
|
|
|
|
Р
| ||
|
а
|
|
в
|
|
Рис. 3.8. Определение основных кинетических параметров в случае однокомпонентного полностью неконкурентного ингибирования фермента | ||
|
а |
|
| |||||
|
|
Рис. 3.9. Определение основных кинетических параметров в случае двухкомпонентного полностью конкурентного взаимозависимого ингибирования |
Рис. 3.10. Определение основных кинетических параметров в случае двухкомпонентного полностью неконкурентного взаимозависимого ингибирования |
| ||||
|
|
б Рис.
3.11.
Определение
основных кинетических параметров в
случае ингибирования фермента
субстратом: а
– в общем виде; б – при высоких
концентрациях субстрата
|
Рис.
3.12. Интегральные координаты для случая
ингибирования фермента продуктом
| |||||
|
|
|
| |||||
|
|
а Рис.
3.13.
Необратимая
инактивация фермента в свободном
виде
|
б Рис.
3.14.
Необратимая
инактивация фермента в составе
фермент-субстратного комплекса
| |||||
|
|
|
| |||||


Рис. 3.15. Определение k2, рКа', рКb' Рис. 3.16. Определение k2, Ks, pKa, pKb


 ;
;
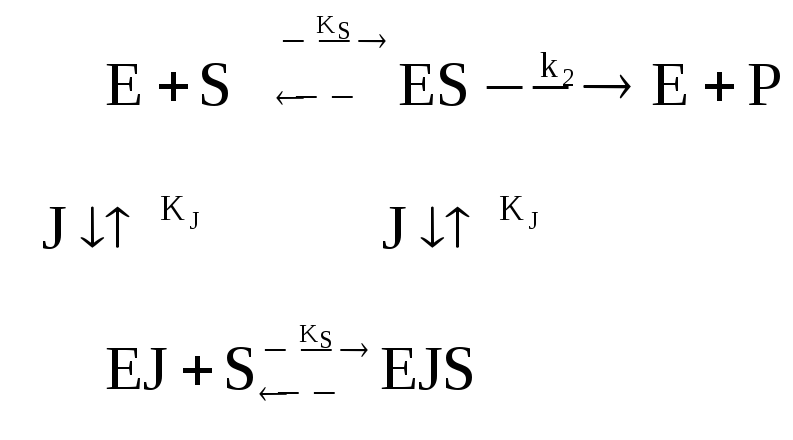 [S]>>[E]
[S]>>[E] ;
; .
.
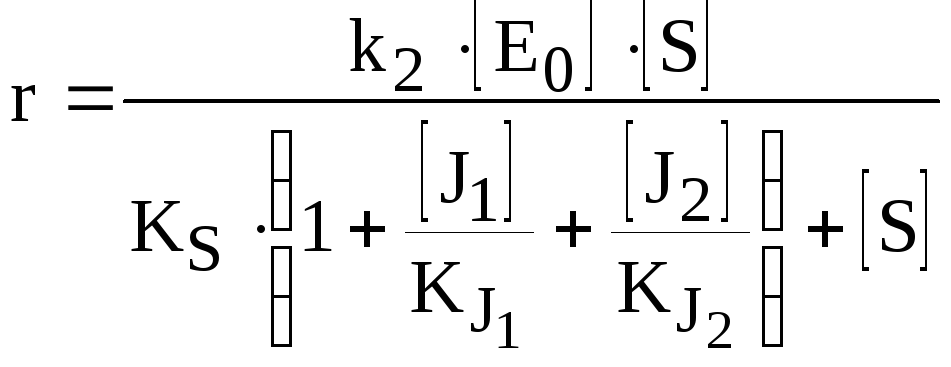 ;
;
 ;
; .
.
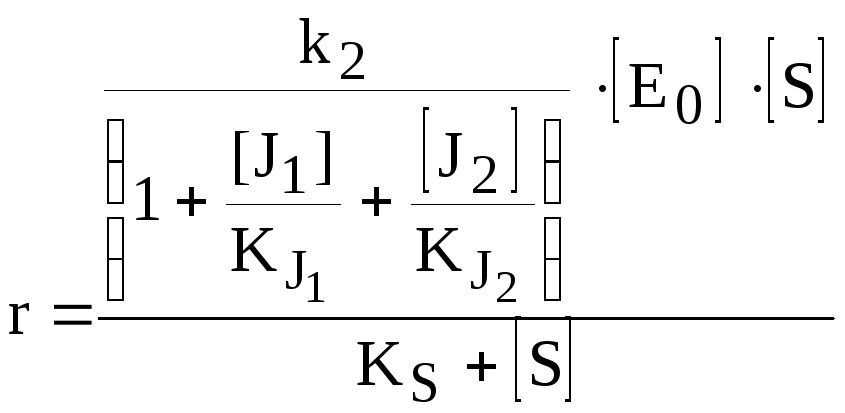 ;
;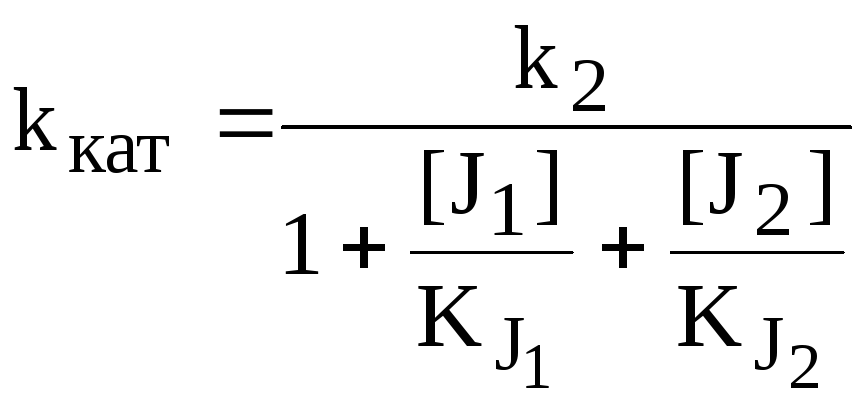 .
.
 .
Если низкие концентрации [S]:
.
Если низкие концентрации [S]:
 .
.
 .
.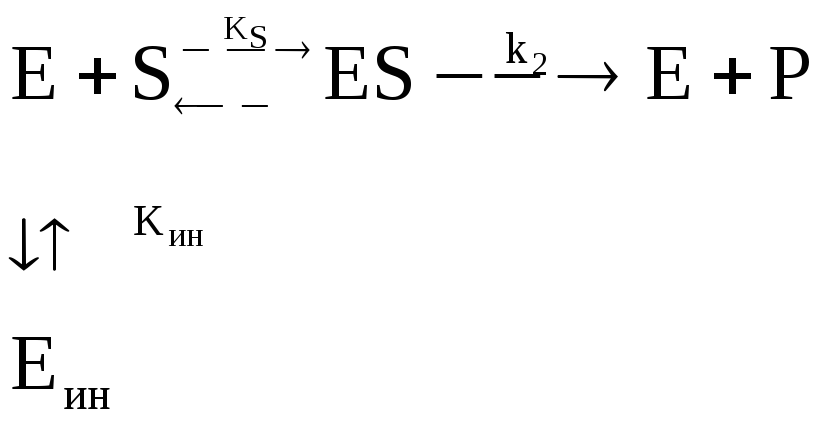

 ;
;


 ;
; ;
;