2. Стехиометрические расчеты биотехнологических процессов

Стехиометрические расчёты биологических процессов имеют не только теоретическое, но и большое практическое значение. На основе стехиометрических закономерностей может быть составлен материальный баланс основной стадии процесса – ферментации или ферментативного превращения, а затем может быть построен и тепловой баланс. Эти расчёты являются базой для проектирования промышленных производств.

С теоретической точки зрения интересным представляется вопрос об энергетической эффективности потребления субстратов клетками микроорганизмов и оценка на этой основе целесообразности осуществления тех или иных процессов. Хотя прямые расчеты изменения свободной энергии в микробиологических процессах затруднены из-за отсутствия сведений о свободной энергии биомассы и многих продуктов, ряд выводов может быть сделан уже на основе общих термодинамических расчётов.

В данном разделе рассмотрено практическое приложение законов стехиометрии и термодинамики к популяциям клеткок как системам более сложного уровня по сравнению с ферментативными биохимическими реакциями, которым был посвящен предыдущий раздел настоящего пособия.

2.1 Стехиометрия и материальный баланс микробиологических процессов

Любой процесс может быть описан стехиометрическим уравнением, связывающим количества исходных веществ и продуктов. Стехиометрическое уравнение любого химического процесса представляет собой равенство, в левой и правой частях которого массы различных веществ суммируются таким образом, что бы число грамм-атомов любого элемента слева или справа от знака равенство совпадало.

Стехиометрическое уравнение простой химической реакции имеет вид:

(1), где

ν_i; ν_i – стехиометрические коэффициенты в рассматриваемой реакции;

I_i – исходные вещества;

P_j – продукты.

Эта зависимость с учётом закона сохранения массы, может быть представлена следующим образом:

(1), где

ν_i – стехиометрический коэффициент i-го компонента в рассматриваемой реакции;

M_i – молекулярная масса i-го компонента.

При этом стехиометрические коэффициенты учитывают количество молей каждого из веществ, вступающих во взаимодействие или образующихся в его результате, при этом коэффициенты продуктов считают положительными, а веществ, вступающих во взаимодействие – отрицательными.

Эта зависимость для общего случая микробиологических процессов, когда популяция микроорганизмов растёт за счёт потребления основного субстрата (источника углерода) и вспомогательных веществ, выделяя при этом ряд продуктов, может быть представлено следующим образом:

(2), где

S_i – питательные вещества (субстраты, компоненты субстрата);

АСБ – абсолютно сухая биомасса;

P_i – продукты.

Следует отметить, что состав биомассы микроорганизмов (АСБ), определяется природой микроорганизмов, компонентами питательной среды, а так же условиями процесса культивирования.

В среднем АСБ дрожжей содержит по массе 46,0 % углерода, 6,8 % водорода, 8,8 % азота, 33,1 % кислорода и 5,3 % остальных элементов. Элементарный анализ бактерий даёт среднее содержание по массе углерода 48,2 %, водорода 7,2 %, азота 9,7 %, кислорода 27,4 %, остальных элементов 7,5 %. Разница элементного состава объясняется тем, что бактериальная биомасса содержит, как правило, больше белковых веществ и нуклеиновых кислот.

Описанные данные массового состава микроорганизмов можно представить в виде брутто-формулы с использованием массовых долей основных элементов в АСБ:

• дрожжи  ;

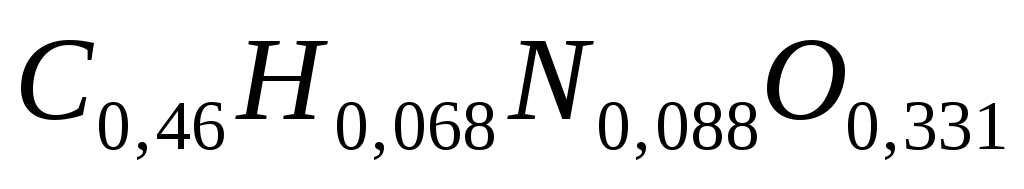• бактерии  .

Данные брутто-формулы биомассы можно пересчитать в мольное отношение элементов из расчёта на 1 атом углерода:

• дрожжи  ;

• бактерии  .

При составлении материального баланса получения АСБ (или продуктов биосинтеза) следует учитывать отличия стехиометрических зависимостей биологических процессов от обычных химических реакций. Они связаны с тем, что любая живая клетка осуществляет одновременно совокупность параллельно протекающих процессов (анаболических и катаболических), которые отражают особенности её метаболизма.

Анаболические процессы приводят к биосинтезу всех структур клетки и некоторых важных продуктов, но в основе своей эти реакции – эндэргонические (G0). Это обстоятельство вынуждает клетку одновременно вести катаболические процессы, которые являются экзэргоническими (G0) и, протекая совместно с анаболическими реакциями, делают возможным их осуществление.

Таким образом, анаболический процесс можно представить в виде схемы:

(3), где

Р_j – побочные продукты биосинтеза, не содержащие углерод.

Соответственно уравнение катаболизма имеет вид:

(4),

Р_j –продукты катаболитческого распада субстрата (при катаболизме накопление АСБ не происходит).

При описании стехиометрических уравнений на первом этапе рассматривают катаболические (4) и анаболические (3) процессы, а по их сумме составляют брутто-уравнение (2) микробиологического процесса.

Для составления стехиометрического уравнения культивирования микроорганизмов необходимо знать не только состав потребляемых исходных веществ, элементарный состав биомассы и состав образующихся в заданном режиме продуктов, но и количественные характеристики процесса, в качестве которых используют расходные коэффициенты.

Расходные коэффициенты – это обычно величины, показывающие необходимый расход питательных субстратов для получения единицы биомассы (отношение масс потреблённых компонентов питательной среды к приросту биомассы). На практике при расчётах обычно используют обратную величину, которую называют экономическим коэффициентом (Y) – отношение прироста биомассы (Δx) к единице потреблённого субстрата (ΔS_i):

[г/г]

(5),

Δx – разница между конечной и начальной концентрациями биомассы по сухому весу (АСБ), г;

ΔS_i – разница между начальной и конечной концентрациями субстрата в питательной среде (зачастую рассматривают только изменение концентрации источника углерода), г.

Иногда пользуются такой характеристикой процесса, как выход биомассы, который представляет собой отношение прироста биомассы, к единице внесённого в питательную среду субстрата. Однако, для составления материального баланса с использованием этого показателя, также необходимо знание степени усвоения субстрата данным микроорганизмом.

Пример 1.

Составьте уравнение реакции катаболизма, анаболизма, брутто-реакции при аэробном культивировании биомассы дрожжей на питательной среде, содержащей в качестве источника азота NH₄OH, углерода – глюкозу, а состав получаемой биомассы – , экономический коэффициент составляет 0,4.

Решение:

1. Составим уравнение анаболизма культивирования дрожжей на глюкозе.

Уравняем углерод с левой и правой стороны в уравнении реакции. Поскольку в приведенной формуле состава биомассы нижние индексы соответствуют массовым долям элементов в составе биомассы, а расчеты необходимо выполнять на 1 г АСБ (абсолютно сухой биомассы), то в 1 г АСБ: m (С)=0,460 г, m (Н)=0,068 г, m (N)=0,088 г, m (O)=0,331 г.

Определим коэффициент, который необходимо поставить перед глюкозой (расчеты производятся с точностью до пятого знака после запятой):

, где Ar_C – относительная атомная масса углерода, 6 - количество атомов углерода в 1 моль глюкозы. Таким образом

Аналогично определяем коэффициент перед аммиаком:

.

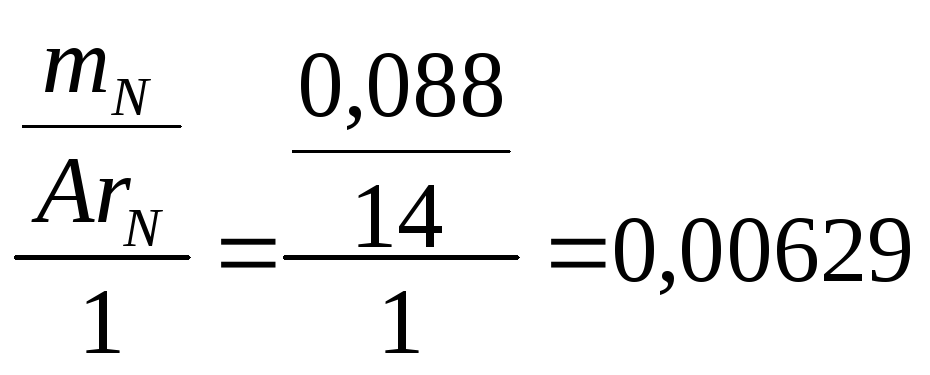При уравнивании водорода учитываем водород во всех соединениях и определяем коэффициент перед водой.

Определим коэффициент перед кислородом:

.

Уравнение анаболизма:

Составим уравнение катаболизма. Исходя из экономического коэффициента, определим количество молей глюкозы, которое пошло на катаболизм.

, тогда , а, следовательно

(180 – молекулярная масса глюкозы).

Уравнение катаболизма:

Брутто-реакция: