Решение

Эмпирические вероятности распределения числа вызовов рассчитываются по формуле

№ п/п	ck	nk
1	0	0	0
2	1	4	0,04
3	2	8	0,08
4	3	14	0,14
5	4	17	0,17
6	5	18	0,18
7	6	15	0,15
8	7	10	0,1
9	8	7	0,07
10	9	4	0,04
11	10	2	0,02
12	11	1	0,01
13	12	0	0
14	-	-	-
15	-	-	-
		100	1

Таблица 2. Эмпирические вероятности распределения числа вызовов

Среднее статистическое значение

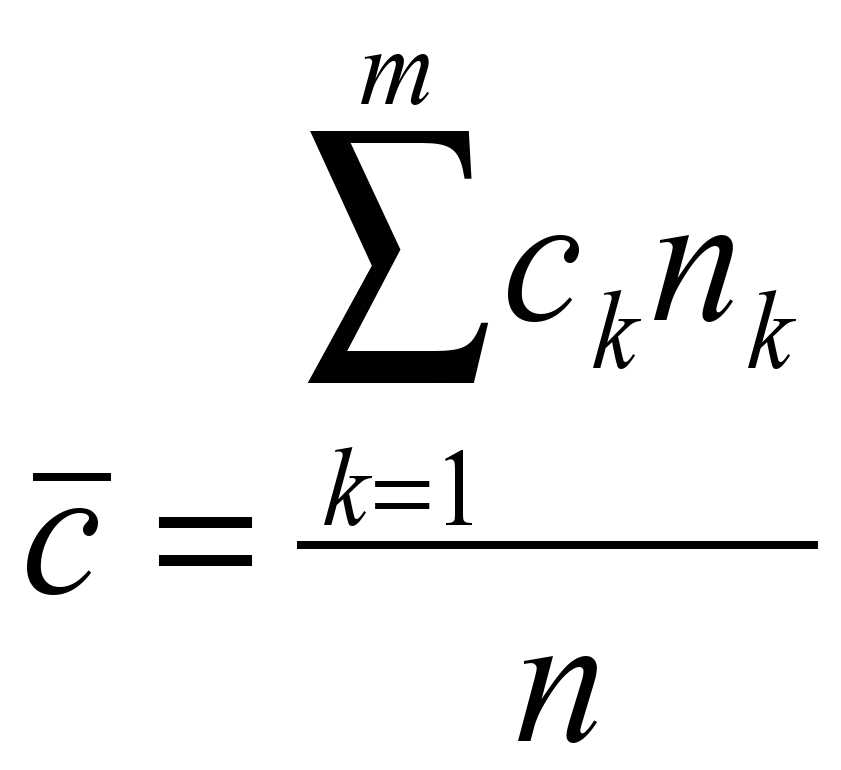, где n – число интервалов наблюдения.

= 5,03

Значения вероятностей распределения Пуассона могут быть определены по справочным таблицам или рассчитаны по формуле

k	ck	Pk(t)
1	0	0
2	1	0,1839397206
3	2	0,1804470443
4	3	0,1680313557
5	4	0,1562934519
6	5	0,1462228081
7	6	0,137676978
8	7	0,1303774322
9	8	0,1240769173
10	9	0,118580076
11	10	0,1137363961
12	11	0,1094298885
13	12	0,1055703835
14	-	-
15	-	-

Таблица 3. Значения вероятностей распределения Пуассона

Число степеней свободы для данной задаче определяется как 

r = m – 2 = 13 – 2 = 11

Мера расхождения 

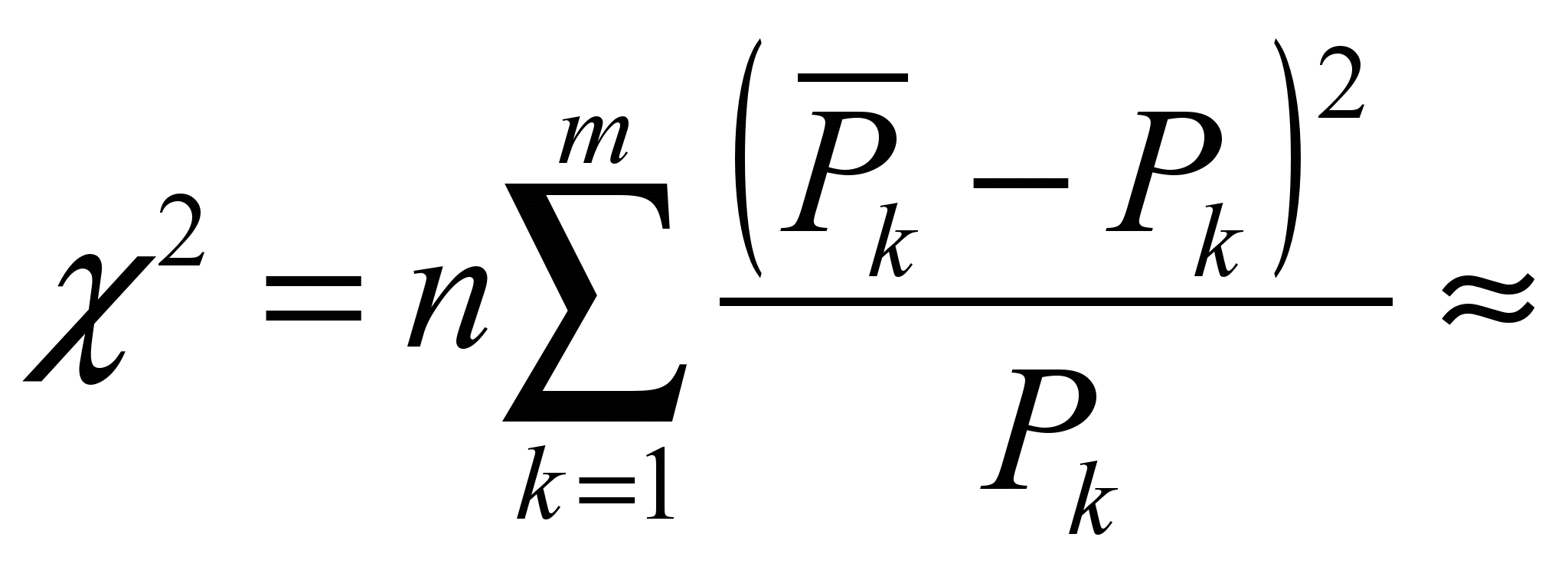54

Из таблицы P(r, ²) = 0,80