Для математической модели м/м/V:

Вероятность задержки вызова P{γ>0} = с_р=0,53

Вероятность ожидания P{γ>t} свыше допустимого времени t для любого поступающего вызова при фиксированных значениях t_доп равна

Для

Для

Для

Вероятность ожидания P₁{γ>t} свыше допустимого времени t для задержанного вызова при фиксированных значениях t_доп равна P₁{γ>t}=

Для

Для

Для

Среднее время ожидания для любого поступившего вызова:

с

Среднее время ожидания для задержанного вызова:

с

Среднее число ожидающих вызовов равно

Эрл

На основании полученных результатов построим график и график

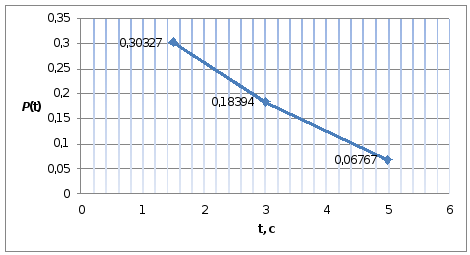
Рисунок 1 - График функции

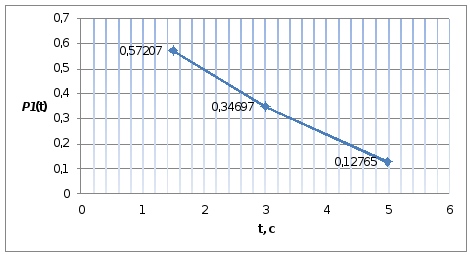
Рисунок 2 - График функции

Для математической модели м/d/V:

Вероятность задержки вызова P{γ>0} = с_р=0,53

Для нахождения вероятности ожидания P{γ>t} свыше допустимого времени t для любого поступающего вызова при фиксированных значениях t_доп воспользуемся кривыми Кроммелина

Для

Для

Для

Вероятность ожидания P₁{γ>t} свыше допустимого времени t для задержанного вызова при фиксированных значениях t_доп равна P₁{γ>t}=

Для

Для

Для

Среднее время ожидания для любого поступившего вызова:

с

Среднее время ожидания для задержанного вызова:

с

На основании полученных результатов построим график и график

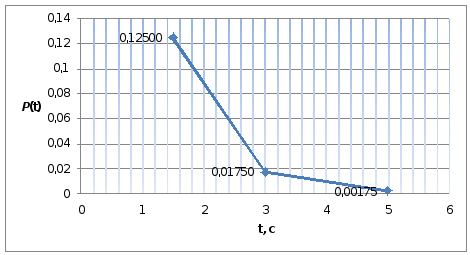
Рисунок 3 - График функции

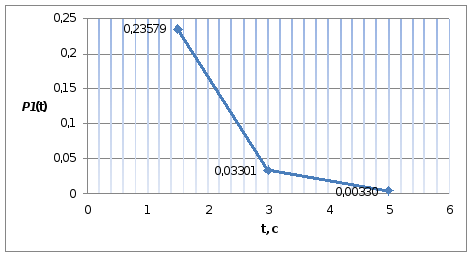
Рисунок 4 - График функции

Вывод

При увеличении в обоих случаях вероятности ожидания обслуживания свыше допустимого времени для любого поступающего и задержанного вызовов снижаются, но в случае с показательным распределением длительности обслуживания вероятность снижается плавно на всей временной оси, а при постоянной длительности занятия сначала резко уменьшается, а потом плавно и медленно уменьшается.

С ростом с_р среднее время ожидания для любого поступившего и для любого задержанного вызова начинает расти. Чем больше с_р, там дольше вызовам приходится ожидать обслуживания.

Задача 1. Исследование процесса поступления сообщений на системы коммутации

Условие: На телефонной станции организовано наблюдение за процессом поступления сообщений. Весь период наблюдения (25 ч), на протяжении которого поток является практически стационарным, разделен на n=100 интервалов длительностью t=15 мин. Для каждого интервала определяется число поступающих сообщений. Данные наблюдений группируются в статистический ряд по m членов, характеризующихся числом интервалов n_k (k = 1, 2, …, m) с одинаковым числом вызовов c_k в интервале

№ п/п	ck	nk
1	0	0
2	1	4
3	2	8
4	3	14
5	4	17
6	5	18
7	6	15
8	7	10
9	8	7
10	9	4
11	10	2
12	11	1
13	12	0
14	-	-
15	-	-
		100

Таблица 1. Исходные данные.

Требуется: Оценить следующие характеристики процесса поступления сообщений.

1. Рассчитать эмпирические вероятности 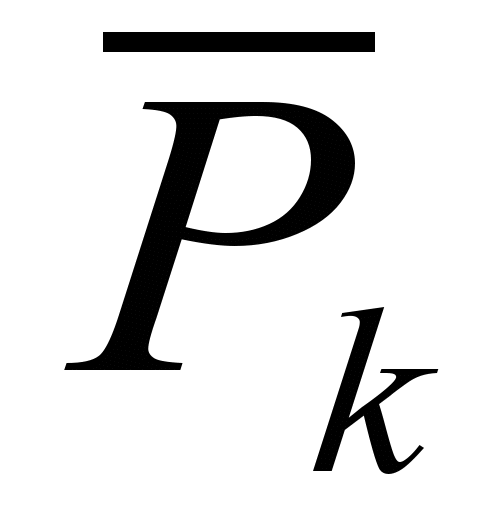 распределения числа вызовов на интервале длительностью t = 15 мин.

2. Рассчитать среднее статистическое значение числа вызовов 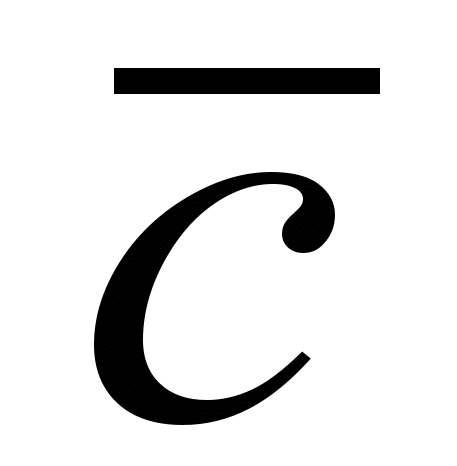 в интервале t=15 мин.

3. Рассчитать вероятности распределения Пуассона P_k на интервале t=15 мин.

4. Рассчитать число степеней свободы r и меру расхождения ² между теоретической вероятностью P_k и эмпирической 

5. Определить соответствие эмпирического распределения числа сообщений в интервале t=15 мин распределению Пуассона