
- •Предположим, что поступающий поток вызовов является примитивным, который характеризуется переменным параметром λi, пропорциональным числу свободных источников (абонентов):
- •Таким образом, приходим к выводу, что наш поток по своим характеристика ближе к простейшему потоку, эта модель описывает его более точно, чем примитивный поток.
- •Для математической модели м/м/V:
- •Для математической модели м/d/V:
- •Решение
Таким образом, приходим к выводу, что наш поток по своим характеристика ближе к простейшему потоку, эта модель описывает его более точно, чем примитивный поток.
Задание 3 Оценка пропускной способности управляющих устройств систем коммутации
Условие
Ступень группового искания (ГИ) координатной АТС с индивидуальными управляющими устройствами (маркерами) для каждого блока комплектуется из s коммутационных блоков. Средняя длительность занятия входа ступени ГИ равна tвх. На ступень искания поступает поток вызовов, создающий нагрузку yвх. Управляющие устройства работают по системе с ожиданием. Средняя длительность занятия одним вызовом управляющего устройства равна h, допустимое время – tдоп.
Необходимо
Оценить следующие характеристики процесса обслуживания.
1. Рассчитать качественные показатели работы управляющих устройств ступени ГИ при постоянной и показательно распределенной длительности обслуживания:
- вероятность задержки вызова P{γ>0};
-вероятность ожидания P{γ>t} свыше допустимого времени t для любого поступающего вызова при фиксированных значениях tдоп;
- вероятность ожидания P1{γ>t} свыше допустимого времени t для задержанного вызова при фиксированных значениях tдоп;
-
среднее время ожидания
![]() для любого поступившего вызова;
для любого поступившего вызова;
-
среднее время ожидания
![]() для задержанного вызова.
для задержанного вызова.
2. Рассчитать
среднее число ожидающих вызовов
![]() (среднюю длину очереди) при показательном
распределении длительности обслуживания.
(среднюю длину очереди) при показательном
распределении длительности обслуживания.
3. По результатам расчетов построить и проанализировать следующие графические зависимости:
- P{γ>t} = f(t) и P1{γ>t} = f(t) для однолинейного пучка, если удельная поступающая нагрузка на управляющие устройства при постоянной длительности обслуживания равна с;
- P{γ>t} = f(t) и P1{γ>t} = f(t) для однолинейного пучка, если удельная поступающая нагрузка на управляющие устройства при показательном распределении длительности обслуживания равна с.
4. Произвести
анализ полученных результатов и сделать
вывод о характере изменений P{γ>t}
и
P1{γ>t})
при
увеличении tдоп
и с,
а также об изменении
![]() и
и
![]() с ростом с
при прочих равных условиях для различных
законов распределения длительности
обслуживания.
с ростом с
при прочих равных условиях для различных
законов распределения длительности
обслуживания.
Значения исходных данных приведены в таблице 1.
Таблица1 – Исходные данные
|
S |
tвх, с |
yвх, Эрл |
h, с |
tдоп1, c |
tдоп2, c |
tдоп3, c |
|
10 |
76 |
560 |
0,66 |
0,99 |
1,98 |
3,3 |
Решение
В соответствии с классификацией Кендала процесс обслуживания простейшего потока вызовов полнодоступным пучком линий при показательном распределении длительности обслуживания и неограниченном числе мест для ожидания соответствует математической модели M/М/v, а тот же процесс при постоянной длительности обслуживания вызова – математической модели М/D/v, причем M/М/v описывается вторым распределением Эрланга, а М/D/v описывается кривыми Кроммелина.
Второе распределение Эрланга и характеристики качества прохождения нагрузки имеют следующий вид:
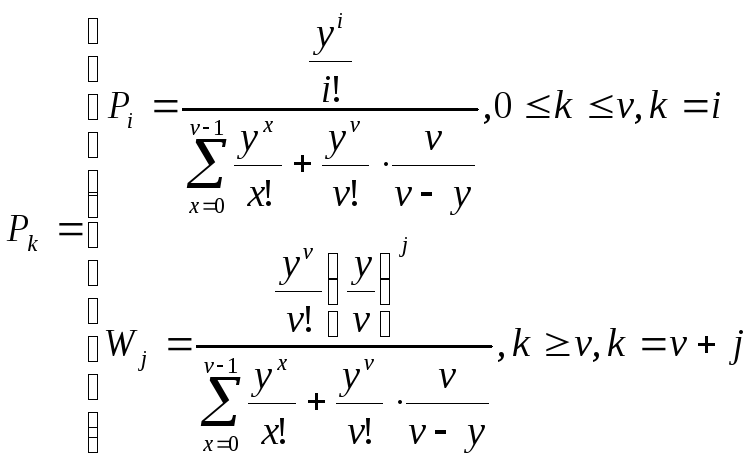
Формулы
![]() и
и
![]() табулированы
и представлены кривыми Кроммелина.
табулированы
и представлены кривыми Кроммелина.
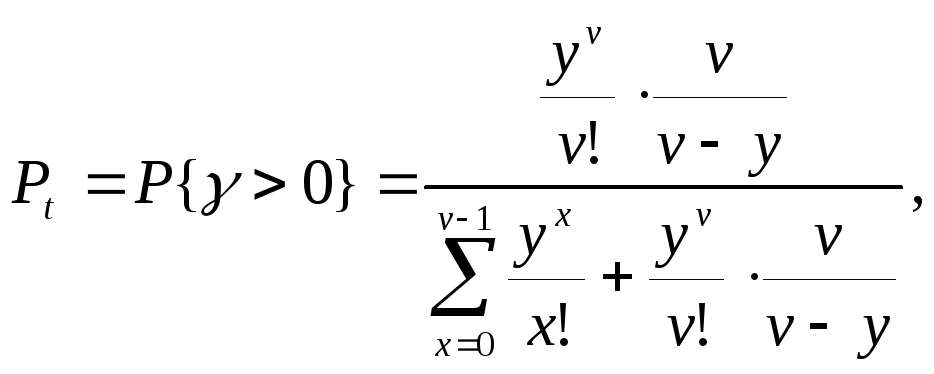
![]()
Определение качественных показателей обслуживания управляющими устройствами поступающей нагрузки должно производиться по расчетному значению нагрузки yр.
Расчетное значение yр обеспечивает требуемое качество прохождения нагрузки с заданной вероятностью ω, отклоняясь от математического ожидания нагрузки y по экспоненциальному закону
![]()
Определим расчетную нагрузку на одно управляющее устройство (маркер) ступени группового искания:
при
v
= 1, y
= c
(![]() )
и P{γ>0}
= f(cp)
)
и P{γ>0}
= f(cp)
yбл = yвх / с = 560/10 = 56 Эрл
ypбл
=![]() =61,045
Эрл
=61,045
Эрл
![]() Эрл
Эрл
Для оценки качественных показателей работы управляющих устройств ступени искания при показательно распределенной и при постоянной длительностях обслуживания необходимо выразить допустимое время ожидания tдоп в условных единицах, численно равных длительности обслуживания маркером одного вызова, в с:
![]()
![]() с
с
![]() с
с
![]() с
с
Далее
необходимо вычислить следующие
характеристики качества прохождения
нагрузки: P{γ>0},
P{γ>t},
P1{γ>t}=![]() с использованием таблиц второй формулы
Эрланга и кривых Кроммелина
с использованием таблиц второй формулы
Эрланга и кривых Кроммелина
