2. Теорема Гаусса.

Использование теоремы Гаусса для расчета полей

(Примеры решения задач)

Поток электрического поля

Пример 2.1.

Два точечных заряда q и –q расположены на расстоянии 2l друг от друга. Найдите поток вектора напряженности через круг радиуса R, плоскость которого перпендикулярна отрезку прямой, соединяющей заряды, и проходит через его середину.

Решение.

Рассмотрим элементарный поток результирующего электрического полячерез бесконечно малую кольцевую зону круга радиусаи ширины(см.рис). В записи потока учтено, что векторперпендикулярен поверхности круга. Выразим напряженность электрического поля через, используя подобие треугольников показанных на рисунке:,

.

Вычисление потока сводится к взятию интеграла:

.

Электрическое поле заряженной сферы

Пример 2.2.

По поверхности сферы радиуса однородно распределен заряд. Определите напряженность электрического поля в произвольной точке пространства вне сферы и внутри нее. Полученный результат представьте на графике, гдепроекция вектора напряженности на осьr, проведенную из центра сферы.

Решение.

Электрическое поле, порождаемое сферически-симметричным распределением заряда сферы, в любой точке пространства направлено вдоль луча от центра сферы и в равноудаленных точках имеет одинаковую величину, т.е. . При таком свойстве симметрии поля в качестве замкнутой гауссовой поверхности возьмем концентрическую сферу радиуса. Поток сквозь выбранную поверхность равен. Согласно теореме Гаусса, он определяется зарядом внутри гауссовой поверхности. Призаряд внутри поверхности равен заряду сферы, а приравен нулю. Поэтому:

Знак заряда определяет знак проекции, а следовательно и направление самого вектора. Он направлен от центра заряженной сферы () или к центру (). Внутри однородно заряженной сферической поверхности электрическое поле отсутствует. График зависимости проекции вектора напряженностина ось, проведенную из центра сферы, показан на Рис. 1 в предположении.

Рис 1

Электрическое поле заряженного шара

Пример 2.3.

По объему шара однородно распределен заряд. Пренебрегая влиянием вещества шара, определите напряженность электрического поля в произвольной точке пространства вне шара и внутри него. Полученный результат представьте на графике, гдепроекция вектора напряженности на осьr, проведенную из центра шара.

Решение.

Поле такой системы зарядов центрально-симметричное, поэтому в качестве гауссовой замкнутой поверхности следует взять концентрическую сферу радиуса .

1) Найдем напряженность электрического поля внутри шара . Векторы напряженностинаправлены по радиусам выбранной сферы, а модули векторовзависят только от расстояниядо центра сферы, то есть, одинаковы по поверхности сферы. Поэтому поток поля векторачерез выбранную сферуможно записать(Рис.2а).

Заряд, охватываемый сферой , равен, где- объемная плотность заряда. Согласно теореме Гаусса. В результате напряженность поля внутри однородно заряженного шара равна:

,

т.е. поле внутри шара возрастает по линейному закону от нуля в центре до значенияна его поверхности.

2) Найдем напряженность электрического поля вне шара . Свойство симметрии поля остается неизменным. Поэтому гауссову поверхность представим концентрической сферойрадиуса(Рис.2а). Согласно теореме Гаусса имеем:, гдезаряд шара. Для величины напряженности поля получим:

.

Поле вне однородно заряженного шара убывает обратно пропорционально.

Объединяя полученные зависимости, запишем:

.

График зависимости проекции вектора напряженности на ось, проведенную из центра шара, представлен на Рис. 2б.

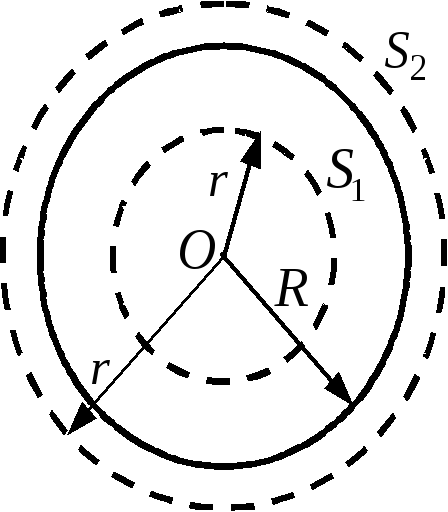
Рис.2а	Рис.2б

Пример 2.4.

Шар заряжен однородно с объемной плотностью . В шаре сделана сферическая полость, положение центра которой характеризуется радиусом-вектором(этот вектор проведен из центра шара в центр полости). Найти полев полости.

Решение.

Представим, что имеем два шара с центрами в точках и, заряженные однородно с объемной плотностьюпервый ивторой. Выберем произвольную точку, которая принадлежит обоим шарам. Воспользовавшись решениемпримера 2.3., для первого шара в точкеполе равно:

().

Для второго шара в точке поле равно:

.

Рис.3

Чтобы определить напряженность поля в полости наложим распределение зарядов двух шаров, как показано на Рис.3. Тогда по принципу суперпозиции найдем поле в полости:

.

Заметим, что поле внутри полости однородно заряженного шара оказывается однородным, а его величина и направление определяется вектором смещения .

Пример 2.5.

Шар радиуса имеет положительный заряд, объемная плотность которого зависит от расстоянияrдо его центра как, где- положительная постоянная. Пренебрегая влиянием вещества шара, найдите модуль вектора напряженности электрического поля внутри и вне шара как функциюr.

Решение.

Поле этой системы зарядов центрально-симметричное, поэтому в качестве замкнутой гауссовой поверхности выберем сферу, концентрическую с шаром.

1) Для нахождения поля вне шара радиус сферы , согласно теореме Гаусса:

,

где полный заряд шара. Чтобы найти, мысленно представим шар в виде набора бесконечно тонких шаровых слоев радиусаширины(Рис.4а). Объем шарового слоя, тогда, а.Интегрируя, получим:

Подставив полученное выражение для в правую часть соотношения для потока, получим напряженность поля вне шара:

.

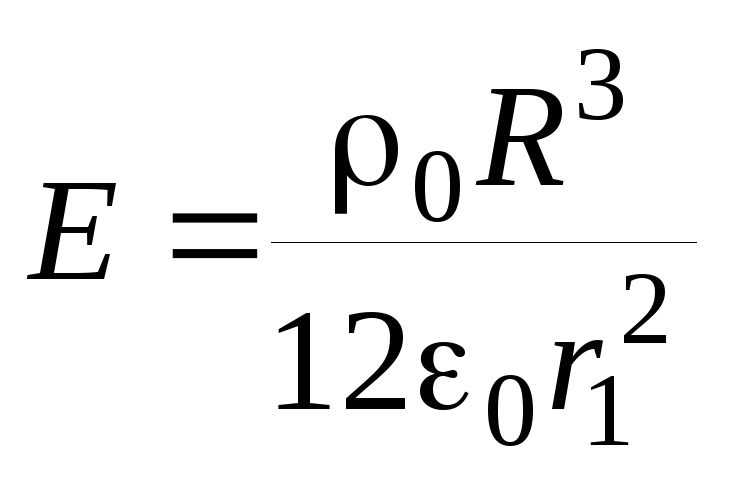2) Найдем напряженность электрического поля внутри шара. В качестве замкнутой гауссовой поверхности снова выберем сферу, концентрическую с шаром, радиус которой(рис.4б).

Согласно теореме Гаусса

,

где заряд внутри выбранной сферы. Величинунайдем также как и в пункте 1), подставив соответствующие пределы интегрирования:

.

Подставив величину заряда в соотношение для потока, найдем:

.

График зависимости проекции вектора на ось, проведенную из центра шара, показан на Рис.4в, из которого видно, что напряженность достигает максимума на расстоянииот центра шара.

Рис.4а	Рис.4б	Рис.4в