Пример 1.11

Система состоит из тонкого заряженного проволочного кольца радиуса и очень длинной однородно заряженной нити, расположенной по оси кольца так, что один из ее концов совпадает с центром кольца. Последнее имеет заряд. На единицу длины нити приходится заряд. Найдите силу, с которой кольцо действует на нить.

Решение.

Разобьем нить на элементарные участки длины dl с зарядом, каждый из которых можно рассматривать как точечный. На каждый точечный зарядкольцо действует с силой

,

где - напряженность электрического поля, создаваемого заряженным кольцом на оси на расстоянииот центра. Согласно результатупримера 1.7

.

Подставим в выражение для величину поля и, проинтегрировав левую часть полученного уравнения отдоF, а правую от 0 до, найдем силу взаимодействия кольца и нити:

.

Учитывая, что , приведем последнее выражение к виду удобному для интегрирования и найдем искомую величину

.

Пример 1.12

Полубесконечный круглый цилиндр радиуса заряжен однородно по поверхности так, что на единицу его длины приходится заряд.

Найдите напряженность электрического поля в центре основания цилиндра.

Решение.

Представим, что цилиндр состоит из набора круглых тонких колец ширины каждое. Точканаходится на оси этих колец.

Воспользуемся формулой для напряженности поля на оси равномерно заряженного кольца (пример1.7):

где – заряд одного кольца. Тогда

Все напряженности в точке, создаваемые кольцами направлены одинаково (против оси). По принципу суперпозиции, имеем:

Пример 1.13

Круглая тонкая пластинка радиуса однородно заряжена с поверхностной плотностью.

Найдите модуль напряженности электрического поля на оси пластинки, как функцию расстояния от ее центра. Рассмотрите предельные случаии.

Решение.

Представим круглую пластинку в виде набора узких концентрических колец радиуса и ширины(см. рис.).

Заряд одного такого элементарного кольца равен:

,

где площадь этого кольца.

Используя формулу для напряженности поля на оси кольца из примера 1.7., запишем напряженность поля в произвольной точкес координатой:

Векторы направлены одинаково для всех колец пластинки (по оси, так как заряд пластинки положительный). Применив принцип суперпозиции для напряженности, найдем:

Построим график зависимости :

Рассмотрим предельные случаи:

1) при - что соответствует полю бесконечной равномерно заряженной плоскости;

2) при , учитывая что, поле пластинки можно привести к виду:

то есть на больших расстояниях поле круглой пластинки соответствует полю точечного заряда, помещенного в ее центр.

П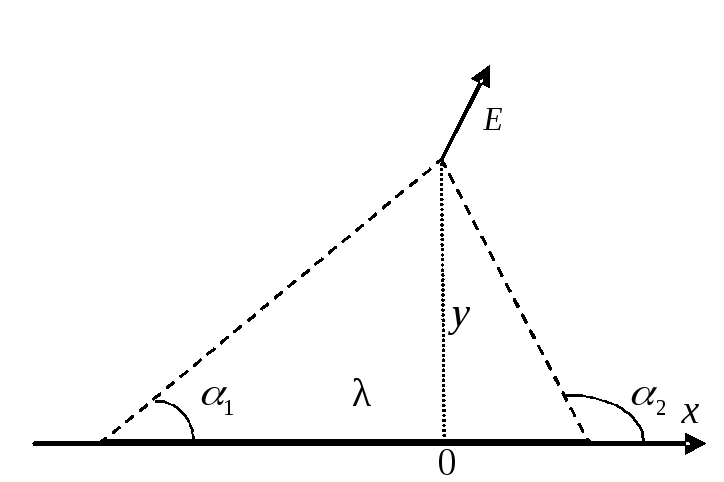ример 1.14

Найти напряженность электрического поля, созданного отрезком тонкой, однородно заряженной с линейной плотностьюнити в точке наблюденияcкоординатами,(см. рис.). Углы с осьюx,под которыми видна точка наблюдения из концов отрезка,и расстояниеy- известны.

Решение.

Вклад в напряженность поля от элемента отрезка dxравен. Поля от разных элементов отрезкаотличаются как величиной, так и направлением. Поэтому для нахождения результирующего поля проинтегрируем проекции элементарных полейи. Для удобства интегрирования выразим переменные величиныrиx через уголпо соотношениям (см.рис.)и,. При этоми для проекцийE_xиE_y получим:

,

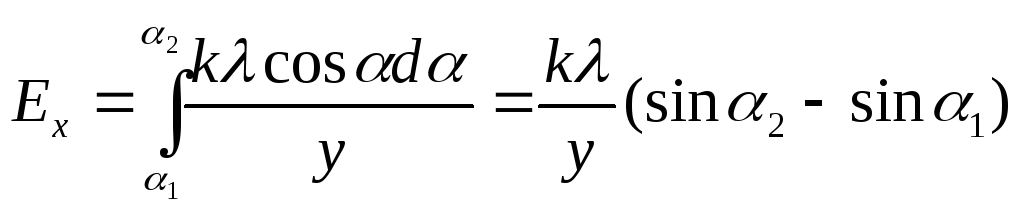Полученные формулы включают в себя все результаты расчета полей однородно заряженных отрезков. Приведем наиболее часто используемые:

Поле на перпендикуляре, проведенном из середины отрезка:

,

Поле бесконечного отрезка:

,,

Поле полубесконечного отрезка в точках плоскости перпендикулярной отрезку и проходящей через его торец:

,

Пример 1.15

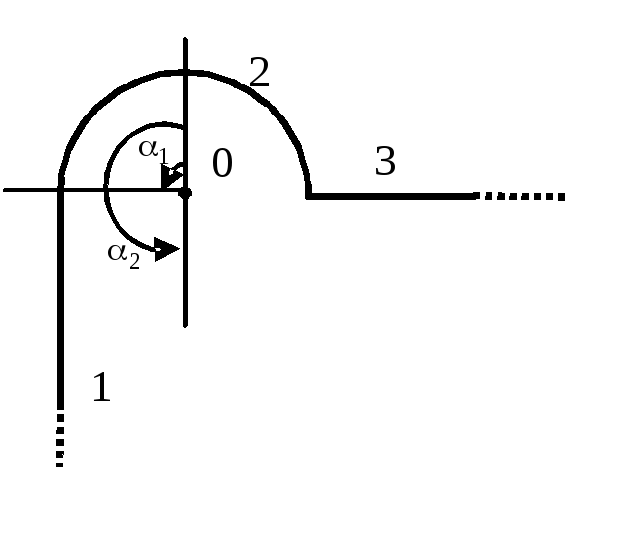Однородно заряженная нить, на единицу длины которой приходится положительный заряд, имеет два полубесконечных прямолинейных и закругленный участки. Найдите модуль напряженности электрического поля в точке 0 для конфигурации, показанной на рисунке.

Решение.Нить, показанная на рисунке, имеет три участка - два прямолинейных полубесконечных (на рисунке участки 1 и 3) и один закругленный (на рисунке участок 2). Для решения задачи воспользуемся принципом суперпозиции полей, создаваемых каждым из трех участков нити в точке 0.

Выберем оси координат так, чтобы начало координат совпадало с точкой 0, а оси xиусовпадали с полубесконечными участками 1 и 3 (рис.).

Напряженность поля полубесконечной нити в точке, лежащей на перпендикуляре к оси нити (участок 1) будет иметь составляющие вдоль осейx иу, которые согласно результатупримера 1.13, проекции которых равны

,

а направления показаны на рисунке.

Согласно результату примеру 1.4, напряженность поля полукольца (участок 2) в точке 0 будет направлена вдоль оси у и равна

(рис.).

Согласно результату задачи 1.13, результирующая напряженность поля полубесконечной нити в точке 0, лежащей на оси нити (участок 3) будет направлена вдоль оси x и равна

(рис.).

Сложив попарно проекции векторов, направленные вдоль осей x иу:

,

,

Найдем величину напряженности в точке 0:

,

то есть модуль вектора напряженности электрического поля в точке 0 равен , а направление вектора противоположно направлению осиу.

16