Пример 4.10.

Точечный электрический диполь развернули в однородном электрическом поле так, что угол между векторами дипольного момента и напряженности поля изменился от ₁ = 90⁰ до ₂ = 30⁰. Во сколько раз уменьшился модуль вектора момента сил, действующих на диполь со стороны электрического поля? Определите работу, произведенную при этом внешними силами.

Решение.

Механический момент, действующий на диполь с дипольным моментом , помещенный в однородное электрическое поле с напряженностью равен:

или ,

где - угол между направлениями векторов и .

Найдем отношение модулей моментов сил, действующих на диполь со стороны электрического поля в первом и втором положении диполя:

.

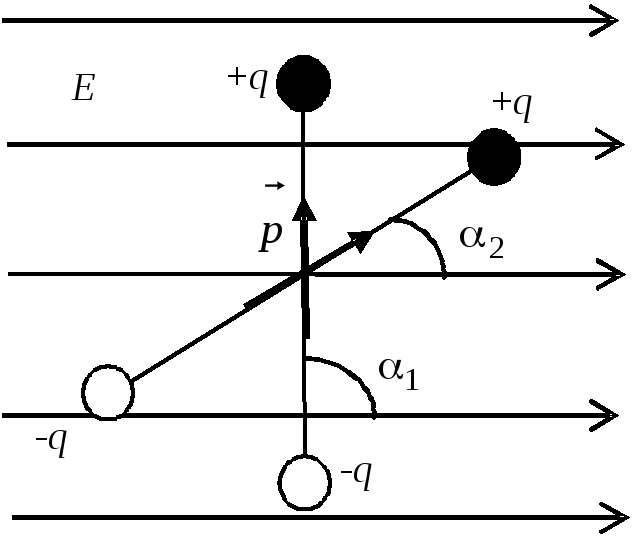
Из положения 1 в положение 2 диполь будет поворачиваться под действием сил поля (рис.7). Поэтому работа внешних сил при этом будет отрицательна.

Рис.7

Элементарная работа при повороте диполь на угол равна:

.

А полная работа при повороте на угол от до :

.

Проинтегрировав правую часть уравнения в пределах от до , найдем работу внешних сил при повороте диполя в постоянном электрическом поле:

.

Пример 4.11.

Точечный электрический диполь с моментом перемещают вдоль пунктирной линии окружности (рис.8) в электрическом поле неподвижного положительного точечного заряда . В какой точке модуль вектора момента сил, действующих на диполь со стороны электрического поля, будет максимальный?

Рис.8

Решение.

Момент сил, действующий на диполь с дипольным моментом , помещенный в электрическое поле с напряженностью равен:

,

а его величина , где- угол между векторами и.

Из рисунка видно, что диполь перемещают в неоднородном электрическом поле точечного заряда, напряженность которого равна:

,

где - радиус окружности.

Поскольку диполь перемещают вдоль окружности, напряженность поля, создаваемого точечным зарядом, в различных точках этой окружности будет одинаковой по величине, но разной по направлению (рис.8). Поэтому, величина модуля вектора момента сил, действующих на диполь со стороны электрического поля, будет зависеть от угла между векторами и , и в тех точках, где синус этого угла будет максимальным, модуль вектора момента сил будет максимальным. Максимальное значение модуля синуса угла равно при значениях угла , поэтому в этих точках модуль вектора момента сил, действующих на диполь со стороны электрического поля, будет максимальный, а его величина равна

,

где r – радиус окружности.

Пример 4.12.

Какую работу против сил электрического поля следует совершить, чтобы перевести диполь с электрическим моментом из положения 1, где напряженность поля равна , в положение 2 с напряженностью (рис.9).

Рис.9

Решение.

Так как поле потенциально, то работу сил поля представим как убыль потенциальных энергий диполя:

,

Где W -потенциальная энергия диполя в электрическом поле равная:

.

Для работы сил поля получим следующее выражение:

.

Работа, совершаемая против сил электрического поля, равна. Заметим, что работа не зависит от величины поля в точке 2.