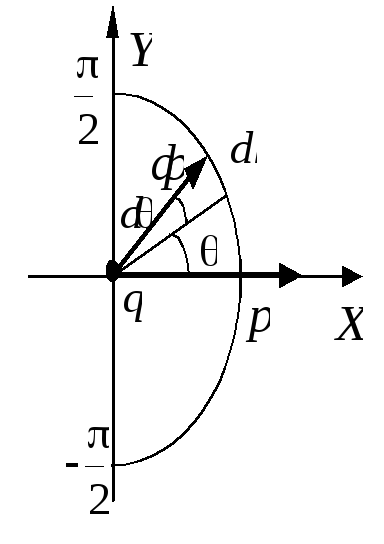
Пример 4.8

Система состоит из заряда , однородно распределенного по полуокружности радиуса а, в центре которой находится точечный заряд (–q) (рис.5). Найдите:

а) электрический дипольный момент этой системы;

б) модуль напряженности и потенциал электрического поля на оси х системы на расстоянии r >> a от нее;

в) модуль напряженности электрического поля на оси y системы на расстоянии r >> a от нее.

Рис.5

Решение.

Разобьем полукольцо на малые элементы с положительными зарядами , а отрицательный заряд, находящийся в центре кольца, на сумму соответствующих малых отрицательных зарядов . Тогда система зарядов и будет представлять собой диполь, дипольный момент которого равен:

,

а направление указано на рис.5. Как видно из рисунка, результирующий дипольный момент системы будет направлен вдоль осив силу симметрии распределения заряда относительно этой оси. Запишем проекцию на эту ось:

.

Приведем полученное уравнение к виду, удобному для интегрирования, учитывая, что и :

.

Проинтегрировав левую часть уравнения от 0 до p, а правую от до , найдем результирующий электрический дипольный момент системы:

.

б) Напряженность поля точечного диполя определяется выражением:

.

Модуль напряженности поля рассматриваемой системы в точке, лежащей на оси диполя (ось х) на расстоянии r >> a () равен:

.

Потенциал электрического поля точечного диполя определяется выражением:

.

Потенциал данной системы в точке, лежащей на оси диполя на расстоянии r >> a () равен:

.

в) модуль напряженности и потенциал электрического поля на перпендикуляре к плечу диполя (ось y) на расстоянии r >> a от нее () соответственно равны:

,

.

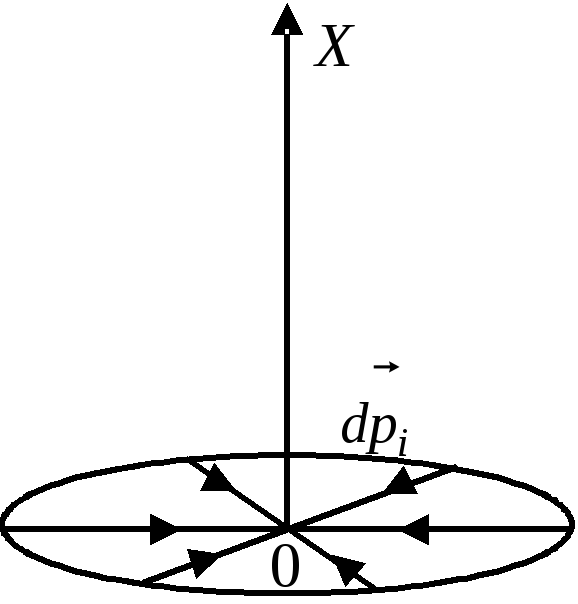
Пример 4.9.

Точечный заряд q расположен в центре кольца радиуса R, по которому равномерно распределен заряд (–q). Определите потенциал и напряженность электрического поля данной системы в точке, расположенной на прямой, проходящей через центр кольца перпендикулярно его плоскости, на расстоянии от центра.

Решение.

Разобьем кольцо на малые элементы с положительными зарядами , а отрицательный заряд, находящийся в центре кольца, на сумму малых отрицательных зарядов . Тогда система малых зарядов и будет представлять собой диполь, дипольный момент которого равен

,

а направление указано на рис.6.

Рис.6

Как видно из рисунка результирующий дипольный момент системы, определяемый как векторная сумма дипольных моментов, будет равен нулю

.

Потенциал электрического поля данной системы в точке, расположенной на прямой, проходящей через центр кольца перпендикулярно его плоскости, на расстоянии от центра, найдем, воспользовавшись принципом суперпозиции:

,

где и потенциалы, создаваемые точечным положительным зарядом и отрицательно заряженным кольцом соответственно.

Пользуясь приближением , преобразуем второе слагаемое в выражении потенциала к виду:

,

и найдем искомый потенциал в точках оси при

.

Воспользовавшись полученной формулой, определим напряженность электрического поля. Проекция вектора напряженности на ось равна:

.