
Семестровый план по Теории функций комплексной переменной для ЭКТ-2, 3-й семестр 2016-2017
.docxУЧЕБНАЯ ДИСЦИПЛИНА
«ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ», ЭКТ-II
-
ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
-
ЛИТЕРАТУРА
|
|
Сборник задач по математике для ВТУЗов. : Учеб. пособие для втузов: В 4-х ч.. Ч. 3: [Векторный анализ; Ряды и их применение; Теория функций комплексной переменной; Операционное исчисление; Интегральные уравнения; Уравнения в частных производных; Методы оптимизации] / Ефимов А.В. [и др.] ; Под ред. А.В. Ефимова, А.С. Поспелова. – 5-е изд., перераб.. - М. : Физматлит, 2009. - 544 с.. - Шифры: 51(076.1) - С-232 |
|
|
И. В. Лавров, А. М. Терещенко. Теория функций комплексной переменной: Учеб. пособие / Министерство образования и науки РФ, Национальный исследовательский университет "МИЭТ". - 2-е изд. - М. : МИЭТ, 2015. - 168 с. - ISBN 978-5-7256-0788-8. 517.53(075.8) - Л-136 |
|
|
Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной [Текст] : Учебник для вузов / Под ред. А.Н. Тихонова, В.А. Ильина, А.Г. Свешникова. - 6-е изд., стер. - М. : Физматлит, 2010. - 336 с. - (Курс высшей математики и математической физики. Вып. 5). - ISBN 978-5-9221-0133-2. 517.53(075.8) - С-245 |
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
-
Я.С. Бугров, С.М. Никольский. Высшая математика [Текст] : Учебник для вузов: В 3-х т. Т. 3: Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного / Я. С. Бугров, С. М. Никольский; Под ред. В.А. Садовничего. - 5-е стер. изд. - М. : Дрофа, 2003. - 512 с. - (Высшее образование. Современный учебник). - ISBN 5-7107-6556-2. 517(075.8) - Б-902
-
Алфимов Г.Л., , Альшина Е.А. Специальные разделы математического анализа [Текст] : Учеб. пособие / Г. Л. Алфимов, Е. А. Альшина ; Министерство образования и науки РФ, Национальный исследовательский университет "МИЭТ". - М. : МИЭТ, 2011. - 216 с. - Имеется электронная версия издания. - ISBN 978-5-7256-0617-1. 517(075.8) - А-537
-
И. Н. Бронштейн, К. А. Семендяев. Справочник по математике для инженеров и учащихся вузов [Электронный ресурс] : Учеб. пособие / - СПб. : Лань, 2010. - 608 с. - Доступ к электронной версии книги открыт на сайте http://e.lanbook.com/. - ISBN 978-5- 8114-0906-8. ЭБС Лань
Для доступа к полнотекстовым ресурсам (Электронный каталог библиотеки МИЭТ) необходимо пройти регистрацию с любого компьютера университета -зайти на главную страницу сайта МИЭТ и совершить переходы «Электронные ресурсы» - «Электронные библиотеки». Выбирая пункт «Электронный каталог библиотеки МИЭТ» вы попадаете на начальную страницу нашей библиотеки. Для авторизации в системе нужно нажать кнопку «Войти» и ввести свои логин (номер электронного пропуска) + пароль.
1.2. ЭЛЕКТРОННЫЕ РЕСУРСЫ
|
-
СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
2.1. ЛЕКЦИОННЫЕ ЗАНЯТИЯ
|
№ |
Содержание |
|
Комплексные числа. Комплекснозначные функции действительной переменной. Кривые и множества точек на комплексной плоскости. Пределы комплексных последовательностей. Функция комплексной переменной (ФКП). Предел, непрерывность ФКП. Л-2, с.5-30 |
|
Производная ФКП. Условия Коши-Римана. Понятие аналитической функции. Свойства аналитических функций. Элементарные функции и их свойства. Л-2, с.30-42 |
|
Интегрирование функции комплексной переменной. Теоремы Коши для односвязной и многосвязной областей. Интегральная формула Коши. Теорема о среднем. Теоремы Морера, Лиувилля. Л-2, с.43-63 |
|
Функциональные ряды. Равномерная сходимость рядов. Свойства равномерно сходящихся рядов. Степенные ряды. Разложение функций в ряд Тейлора. Ряд Лорана. Изолированные особые точки. Л-2, с.64-85 |
|
Вычеты, теоремы о вычетах. Применение теории вычетов для вычисления интегралов. Л-2, с.86-109 |
|
Преобразование Лапласа. Основные теоремы операционного исчисления. Л-2, с.110-123 |
|
Обратная задача операционного исчисления. Приложения операционного исчисления. Л-2, с.123-136 |
-
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
|
№ |
Содержание |
|
Комплексные числа. Множества точек на комплексной плоскости. Функции комплексной переменной (ФКП), выделение действительной и мнимой частей. Выдача ДЗ. Л-1,гл.13: № 27,43,44,46,49Л-2: 1.1(а,в), 1.2(а,в,д), 1.3(а,в), 1.4(а,в), 2.1(а,в,д,е,м), 2.6(а,в,д,з), 3.1(а,в,д,е,к), 3.2(а), 3.3 На дом: Л-1, гл.13: №№ 28,45,47,50; Л-2: 1.1(б,г), 1.2(б,г,е,ж,з), 1.3(б,г), 1.4(б,г), 2.1(б,г,ж,з,к,н), 2.6(б,г,е,ж), 3.1(б,г,ж,и,л), 3.2(б) |
|
Основные элементарные функции комплексной переменной. Л-1,гл.13: № 54,56,59,87; Л-2: 3.4(а,в,д,ж,и) На дом: Л-1, гл.13: №№ 55,60,90; Л-2: 3.4(б,г,е,з) |
|
Предел и непрерывность ФКП. Дифференцирование ФКП. Условия Коши-Римана. Восстановление действительной или мнимой части аналитической функции. Самостоятельная работа 1 (45 мин): «Действия с комплексными числами, вычисление значений ФКП, нахождение действительной и мнимой частей, проверка аналитичности». Прием ДЗ (1 часть, задания 1-4). Л-1, гл.13, № 92,94,96,98,100,107,121,123,144,148, 152Л-2: 3.5(а,б,г), 3.6(а,в,г), 3.7(а), 3.8(а) На дом: Л-1, гл.13, № 93,95,97,99,101,108,122,124,145,149,154; Л-2: 3.5(в,д), 3.6(б,д,е), 3.7(б), 3.8(б) |
|
Интегрирование функций комплексной переменной. Интегральная формула Коши Л-2: 4.1(а, б, д, ж), 4.2 (а, в), 4.3 (а, в, д, е, ж, о, с) На дом: Л-2: 4.1(в,г,е), 4.2 (б,г), 4.3 (б, г, з, и, к, л, п) |
|
Разложение функций в степенные ряды и ряды Лорана. Изолированные особые точки. Самостоятельная работа 2 (45 мин) «Интегрирование ФКП. Разложение в ряды». Л-2: 5.2(а,б,д,ж,и,м), 5.3(а,в), 6.1(а,б,г,з) На дом: Л-2: 5.2(в,г,е,з,к,л), 5.3(б,г), 6.1(в,д,е,ж) |
|
Вычеты и их приложения. Вычисление контурных и определённых интегралов с помощью теории вычетов. Прием ДЗ (2 часть, задания 5-7). Л-2: 6.2(а,б,д,з), 6.3(а,б,в,е,к,н), 6.4(а,г,д,е,к,л,о) На дом: Л-2: 6.2(в,г,е,и), 6.3(б,д,ж,л,о), 6.4(б,з,и,н) |
|
Преобразование Лапласа. Нахождение изображений, оригиналов. Решение задачи Коши для обыкновенного дифференциального уравнения с помощью операционного исчисления. Л-2: 7.1(а,в,е,и,к,н), 7.2(а,б,д,ж,и,к,м), 7.3(а,в,д) На дом: Л-2: 7.1(б,д,ж,з,л,п), 7.2(в,г,е,з,л,н), 7.3(б,г,е) |
|
Приложения операционного исчисления для решения задач математической физики. Прием ДЗ (3 часть, задания 8-10). Л-2: 7.4(а,б,д) На дом: Л-2: 7.4(в,г) |
|
Итоговая контрольная работа. |
-
ДОМАШНИЕ ЗАДАНИЯ
|
№ |
Содержание |
|
Задание 1 |
Вычислить комплексное выражение. Л-2 |
|
Задание 2 |
Найти все значения корня из комплексного числа. Л-2 |
|
Задание 3 |
Изобразить множество точек на плоскости. Л-2 |
|
Записать числа в алгебраической форме. Л-2 |
|
Выяснить характер особых точек. Л-2 |
|
Разложить
функцию
|
|
Вычислить интегралы, используя теорию вычетов. Л-2 |
|
Найти изображения функций. Л-2 |
|
Найти оригиналы для заданных изображений. Л-2 |
|
Методами операционного исчисления решить задачу Коши. Л-2 |
-
САМОСТОЯТЕЛЬНАЯ РАБОТА
(адрес: http://orioks.miet.ru/oroks-miet/srs.shtml - кафедра ВМ-2 - логин: u<номер студенческого билета>, пароль: <дата рождения> в формате ДД.ММ.ГГГГ)
|
№ |
Темы ЭМИРС |
Используемый ПП |
|
Тема «Специальные разделы математического анализа». Теория функций комплексной переменной. |
ОРОКС |
|
Тема «Специальные разделы математического анализа». Особые точки и разложения в ряды. |
ОРОКС |
|
Тема «Специальные разделы математического анализа». Теория вычетов. |
ОРОКС |
|
Тема «Специальные разделы математического анализа». Операционное исчисление. |
ОРОКС |

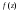 в ряд Лорана. Л-2
в ряд Лорана. Л-2