
3 семестр ЭКТ / Физика. Оптика / Методические материалы и лекции / Luks2
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
КОНСПЕКТЫ ЛЕКЦИЙ ПО ФИЗИКЕ
Часть 2. Волновые процессы. Волновая и квантовая оптика. Квантовая механика. Многоэлектронные атомы
Методические указания для студентов дневной формы обучения машиностроительного факультета
Составитель Р. К. Лукс
Ульяновск
УлГТУ
2013
1
УДК 53 (076) ББК 22.2я7
К32
Одобрено секцией методических пособий научно-методического совета университета
Конспекты лекций по физике. В 2 ч. Ч. 2. Волновые процессы. К32 Волновая и квантовая оптика. Квантовая механика.
Многоэлектронные атомы : методические указания для студентов машиностроительного факультета / сост. Р. К. Лукс. – Ульяновск :
УлГТУ, 2013. – 67 с.
Сборник конспектов лекций по физике составлен в соответствии с типовой программой общего курса физики и федеральных государственных образовательных стандартов высшего профессионального образования по направлениям подготовки:
19020165 – Наземные транспортно-технологические комплексы,
19060062 – Автомобили и автомобильное хозяйство,
15070062 – Машины и обработка металлов давлением,
15190062 – Конструкторско-технологическое обеспечение машиностроительных производств.
Конспекты лекций включают теоретический материал, позволяющий студентам в компактной форме получить достаточную информацию о физических явлениях и закономерностях, необходимых для развития физического мышления и подготовки научной базы, без которой невозможно успешное решение профессиональных задач.
УДК 53 (076) ББК 22. 2я7
© Лукс Р. К., составление, 2013 © Оформление. УлГТУ, 2013
2
СОДЕРЖАНИЕ |
|
Лекция 1 |
|
1.1. Волны. Плоские и сферические волны............................................................................ |
5 |
1.2. Поток энергии волны......................................................................................................... |
7 |
1.3. Групповая скорость волны................................................................................................ |
8 |
Лекция 2 |
|
2.1. Интерференция волн.......................................................................................................... |
9 |
2.2. Стоячие волны................................................................................................................... |
10 |
2.3. Звуковые волны................................................................................................................. |
12 |
2.4. Эффект Доплера................................................................................................................ |
12 |
2.5. Электромагнитные волны ................................................................................................ |
14 |
2.6. Энергия электромагнитной волны. Вектор Умова – Пойнтинга.................................. |
15 |
Лекция 3 |
|
3.1. Отражение и преломление света. Полное отражение.................................................... |
16 |
3.2. Тонкая линза. Формула линзы......................................................................................... |
18 |
3.3. Основные фотометрические характеристики................................................................. |
21 |
3.4. Поляризация света. Виды поляризации.......................................................................... |
23 |
3.5. Поляризация света при отражении от границы раздела двух диэлектриков.............. |
24 |
3.6. Двойное лучепреломление............................................................................................... |
25 |
3.7. Поляризаторы. Закон Малюса ......................................................................................... |
26 |
Лекция 4 |
|
4.1. Интерференция световых волн. Когерентные источники............................................. |
27 |
4.2. Пространственная и временная когерентность.............................................................. |
29 |
4.3. Интерференция на тонкой пленке................................................................................... |
30 |
4.4. Практическое применение интерференции. Интерферометры.................................... |
31 |
Лекция 5 |
|
5.1. Дифракция света. Принцип Гюйгенса – Френеля. Метод зон Френеля...................... |
33 |
5.2. Дифракция Френеля на круглом отверстии.................................................................... |
35 |
5.3. Дифракция Фраунгофера на одной щели ....................................................................... |
36 |
5.4. Дифракционная решетка .................................................................................................. |
37 |
5.5. Дифракция рентгеновских лучей................................................................................... |
39 |
3
Лекция 6 |
|
6.1. Взаимодействие света с веществом................................................................................. |
40 |
6.2. Тепловое излучение. Закон Кирхгофа............................................................................. |
41 |
6.3. Законы теплового излучения............................................................................................ |
43 |
Лекция 7 |
|
7.1. Внешний фотоэффект. Законы фотоэффекта................................................................. |
45 |
7.2. Эффект Комптона.............................................................................................................. |
46 |
7.3. Природа электромагнитного излучения ......................................................................... |
47 |
7.4. Опыты Резерфорда. Планетарная модель атома............................................................ |
47 |
7.5. Постулаты Бора. Опыты Франка и Герца....................................................................... |
48 |
Лекция 8 |
|
8.1. Спектры атома водорода по теории Бора....................................................................... |
50 |
8.2. Волны де Бройля. Опыты, подтверждающие волновые свойства частиц................... |
52 |
8.3. Соотношения неопределенностей Гейзенберга............................................................. |
53 |
Лекция 9 |
|
9.1. Вероятностный смысл волн де Бройля. Волновая функция......................................... |
55 |
9.2. Уравнение Шредингера.................................................................................................... |
55 |
9.3. Микрочастица в прямоугольной потенциальной яме |
|
с бесконечно высокими стенками........................................................................................... |
56 |
Лекция 10 |
|
10.1. Прохождение частиц через потенциальный барьер..................................................... |
58 |
10.2. Орбитальный момент импульса и магнитный момент электрона |
|
в классической и квантовой механике................................................................................... |
59 |
10.3. Опыты Штерна и Герлаха. Спин электрона................................................................. |
61 |
Лекция 11 |
|
11.1. Состояние электрона в атоме. Принцип Паули. |
|
Структура многоэлектронного атома.................................................................................... |
62 |
11.2. Рентгеновское излучение ............................................................................................... |
64 |
11.3. Энергия молекулы........................................................................................................... |
65 |
Библиографический список..................................................................................................... |
67 |
4
Лекция 1
1.1.Волны. Плоские и сферические волны
Волновые процессы наблюдаются в упругих средах. Под упругой средой понимают среду, между частицами которой действуют упругие силы. Если какую либо частицу среды заставить совершать колебания, то за счет действия упругих сил в колебательное движение приходят сначала ближайшие к ней частицы, затем соседние с этими частицами и т. д. Так в колебательный процесс вовлекаются все новые и новые частицы, то есть в среде распространяется упругая волна. Этот процесс сопровождается переносом энергии от источника колебаний, причем переноса частиц в направлении движения волны не происходит – они совершают колебания около своих положений равновесия.
Различают продольные и поперечные волны. В продольной волне частицы среды совершают колебания вдоль вектора скорости распространения волны, а в поперечной – перпендикулярно к нему.
Введем характеристики, описывающие волновой процесс, на примере гармонической волны, в которой частицы среды совершают гармонические колебания
около своих положений равновесия с циклической частотой ω.
1.Фронт волны – геометрическое место точек, до которых дошел волновой процесс.
2.Волновая поверхность – геометрическое место точек, колеблющихся в одинаковой фазе.
3.Период волны – время одного полного колебания частиц среды.
4.Длина волны λ – расстояние, которое проходит волна за один период, или минимальное расстояние между частицами среды, совершающими колебание с разностью фаз ∆φ = 2π.
Форма волновой поверхности и фронта волны зависят от условий возникновения и распространения волны. По виду волновых поверхностей выделяют плоские и сферические волны.
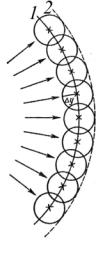
Часто при решении задач о распространении волн надо строить волновой фронт для некоторого момента времени по волновому фронту, заданному для начального момента времени. Это можно сделать с помощью метода, называемого принципом Гюйгенса. Согласно Гюйгенсу,
каждая точка среды, до которой дошла волна, становится источником вторичных волн, и фронт каждой вторичной волны представляет собой сферу, огибающая фронтов вторичных волн определяет новое положение фронта волны. На рис. 1.1 фронт волны в некоторый момент времени t занимает положение 1, а через промежуток времени ∆t – положение 2.
Уравнением упругой волны называют функцию ξ(х, у, z, t), которая определяет смещение любой частицы среды с координатами (х, у, z) относительно своего положения равновесия в произвольный момент времени t.
Выведем уравнение плоской гармонической волны, распространяющейся в положительном направлении оси Ох. Как известно, в плоскости фронта волны – уОz – и параллельных ей плоскостях, все частицы совершают колебания в одинаковых фазе, поэтому в уравнении волны будет отсутствовать зависимость от координат у и z: ξ(х, у, z, t) = ξ(х, t). Пусть в момент времени t = 0 частицы с координатой х = 0, расположенные в плоскости уОz, начинают совершать колебания по закону
ξ(0, t) = А cos (ωt + φ0). |
(1.1) |
5
Частицы с координатой х > 0 начнут совершать колебания только после прихода к
ним волны. Для этого требуется время τ = х/v, и поэтому уравнение колебаний для таких точек примет вид:
( x,t) Acos( (t ) 0 ) Acos( t |
x 0 ) Acos( t kx 0 ). |
(1.2) |
|
v |
|
Уравнение (1.2) представляет собой уравнение плоской гармонической волны, распространяющейся в положительном направлении оси Ох. В эту формулу входит
волновое число k, которое связано с циклической частотой ω, скоростью распространения волны v и ее длиной волны соотношением
k |
2 . |
(1.3) |
v |
|
|
Формула (1.3) определяет модуль волнового числа k . Направление вектора k совпадает с |
||
направлением скорости распространения бегущей волны. |
v волны представляет собой |
|
Покажем, что входящая в формулу (1.2) скорость |
||
скорость движения фиксированного значения фазы волны – фазовую скорость. Действительно,
t kx |
0 |
const |
, |
d |
k |
dx |
kv |
0 , v |
|
, (1.4) |
|
|
|
|
dt |
|
dt |
|
|
k |
|
что согласуется с формулой (1.3).
Волновым уравнением называют уравнение, решением которого является уравнение волны ξ(х, у, z, t). Найдем волновое уравнение для волновой функции (1.2). Если взять частные производные по координате хи времени t от ξ(х, у, z, t):
|
A sin( |
t kx |
|
|
|
), |
2 |
|
A 2 |
cos( |
t kx |
|
|
), |
||||||||
|
0 |
|
|
2 |
0 |
|||||||||||||||||
t |
t |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Ak sin( |
t kx |
|
0 |
), |
2 |
|
Ak 2 cos( |
t kx |
0 |
), |
|
|
|||||||
|
x |
x |
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
то тогда волновое уравнение принимает вид:
2 |
|
1 |
2 |
(1.5) |
x 2 |
|
t 2 . |
||
v 2 |
Оказывается, что решением этого уравнения, кроме плоской гармонической волны, бегущей в положительном направлении оси Ох, является также плоская гармоническая волна, распространяющаяся в отрицательном направлении оси Ох
ξ(х, t) = A cos (ωt + kx +φ0).
Для плоской гармонической волны, распространяющейся в произвольном направлении, которое можно задать радиусом-вектором r , уравнение волны и волновое
уравнение запишутся следующим образом |
|
|
|
|
|
|
|
2 |
2 |
2 |
|
1 2 |
(1.6) |
||
x 2 y 2 z 2 |
|
|
|
||||
v 2 t 2 , |
|||||||
|
|||||||
ξ( r , t) = A cos (ωt - k r |
+φ0). |
(1.7) |
|||||
Можно показать, что волновое уравнение (1.6) удовлетворяет также и уравнению сферической волны
6
ξ( r , t) = A(r) cos (ωt - k r +φ0). |
(1.8) |
Это уравнение отличается от уравнения плоской гармонической волны тем, что для сферической волны амплитуда А будет зависеть от расстояния r между точечным источником колебаний и рассматриваемой точкой в пространстве, а именно амплитуда
сферической волны обратно пропорциональна расстоянию r. |
|
||
A ( r ) |
A0 |
, |
(1.9) |
r |
|
||
где А0 – амплитуда волны на расстоянии 1 м от источника сферической волны.
1.2. Поток энергии волны
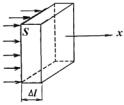
При распространении волн частицы среды не переносятся вместе с волной. Процесс распространения волны в каком-либо направлении в среде сопровождается переносом энергии колебаний в этом направлении. Допустим, что S часть фронта плоской волны распространяющейся в направлении оси Ох в некоторый момент времени t
(рис. 1.2). По истечении времени ∆t фронт волны переместится на расстояние ∆l = v∆t, вследствие чего частицы среды в объеме ∆V = S∆l приводятся в
колебательное движение. Они будут обладать энергией
∆W = w∆V = wvS∆t,
где w – объемная плотность энергии. Можно утверждать, что за время |
|
|
∆t среда через площадку S получила энергию wvS∆t. Таким образом, за |
Рис. 1.2 |
|
единицу времени через площадку S прошла энергия |
||
|
||
d Ф wS l wSv . |
|
|
t |
|
Величина dФ есть поток энергии волны через площадку S (S ориентируют перпендикулярно к направлению распространения волны). Плотностью потока энергии называют энергию, проходящую за единицу времени через единицу площадки, перпендикулярной к направлению распространения волны:
|
|
|
|
|
j |
|
w v . |
|
|
|
|
(1.10) |
|
Этот |
|
вектор |
называют |
вектором Умова |
и |
Пойнтинга. |
Учитывая, |
что |
|||||
w n |
mu m |
2 |
, где n – концентрация частиц среды, um = Аω – амплитуда скорости |
||||||||||
|
|
||||||||||||
2 |
|
|
|
|
|
|
|
|
mA 2 2 |
|
|
|
|
колебаний |
частиц |
среды, |
плотность энергии |
w |
n |
, а |
j ~ |
2 |
|||||
2 |
A . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Распространяющиеся волны характеризуют понятием интенсивность волны I, которая
пропорциональна среднему значению плотности потока, а, следовательно, I ~ A2 .
В сферической волне, вызванной точечным источником колебаний, плотность потока энергии убывает обратно пропорционально квадрату расстояния от источника колебаний. Для доказательства допустим, что источник колебаний ежесекундно отдает в
окружающую среду одну и ту же энергию, равную W. Эта энергия равномерно
7
распределяется по шаровой поверхности фронта волны S = 4πr2, поэтому через единицу площади этой поверхности в единицу времени проходит энергия
j |
|
W |
, т. е. j ~ 1/r2 , а А ~ 1/r (см. 1.9). |
|
4 |
r 2 |
|||
|
|
1.3. Групповая скорость волны
Все реальные волны в той или иной степени отличаются от синусоидальных волн, так как энергия колебательного движения частично превращается в другие виды энергии, что ведет к уменьшению амплитуды колебаний по мере распространения волны.
Уравнение плоской реальной волны можно записать в такой форме:
ξ(х, t) = А0 е-γх cos (ωt – kx +φ0), |
(1.11) |
где A0 е-γх – амплитуда волны, γ – коэффициент затухания. Эту волну можно представить как волну, полученную от наложения двух или большего количества синусоидальных волн с близкими частотами. Такую несинусоидальную волну называют группой волн или волновым пакетом.
В качестве примера рассмотрим простейший волновой пакет, образованный двумя плоскими продольными синусоидальными волнами, распространяющимися вдоль оси Ох.
Пусть амплитуды этих волн одинаковы, начальные фазы φ10 = φ20 = 0, а частоты и волновые числа несколько различны, но близки друг к дугу:
ξ1 = A0 cos (ω1t – k1x ), ξ2 = A0 cos (ω2t – k2x ).
Для результирующей волны
ξ = ξ1 + ξ2 = 2А0 cos(∆ωt - ∆kx) cos(ωt - kx),
где |
1 |
2 |
, |
2 |
1 |
, k |
|
k 1 k 2 |
, k |
|
k 2 k 2 . |
|
|
2 |
|
|
2 |
|
|
2 |
|
|
2 |
Таким образом, результирующая волна является плоской волной, циклическая
частота ω и волновое число k которой равны полусумме соответственно циклических частот и волновых чисел синусоидальных волн, образующих пакет. Однако амплитуда
этой волны не постоянна, а зависит от координаты хи времени t:
A = 2A0 cos (∆ωt - ∆kx), |
(1.12) |
где ∆ωt - ∆kx = φА – фаза амплитуды распространяющейся волны. Дифференцируя выражение для φА в предположении, что φА= const, получим:
u dxdt k ,
Или в пределе, когда ∆ω, а следовательно, и ∆k стремятся к нулю:
8
|
|
|
|
|
|
u d . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
dk |
2 |
|
|
|
|
|
|
2 |
d |
|
|
|
Учитывая, что k |
и dk |
d |
: u |
|
. Так как |
|||||||||||
|
|
2 |
|
|
|
d |
|||||||||||
|
|
2 |
|||||||||||||||
|
2 |
|
2 v |
, где v – фазовая скорость волны, то |
|
|
|
|
|
||||||||
|
Т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
2 |
|
2 |
|
dv |
|
и |
|
|
|||
|
|
|
|
|
d |
|
d |
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
u v |
dv |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
d . |
|
|
|
|
(1.13) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скорость u называют групповой скоростью пакета волн. В случае отсутствия
дисперсии волн в среде (т. е. когда dv/dλ = 0) их фазовые скорости v одинаковы и не зависят от λ. Поэтому в таких средах групповая скорость волн совпадает с их фазовой скоростью.
Лекция 2
2.1. Интерференция волн
Если под действием проходящей волны свойства среды не меняются, то для волн в этой среде применим принцип суперпозиции (наложения). При распространении в этой
среде нескольких волн, каждая из которых распространяется так, как будто другие волны отсутствуют, а результирующее смещение частиц среды в любой момент времени равно геометрической сумме смещений, которое получают частицы, участвуя в каждом из волновых процессов. Накладывающиеся волны, имеющие одинаковую частоту и постоянную во времени разность фаз, называют когерентными.
При наложении когерентных волн возникает явление интерференции.
При этом явлении в пространстве наложения волн возникает перераспределение энергии.
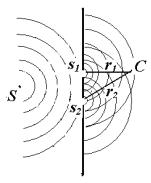
Возьмем точечный источник S (рис. 2.1), от которого распространяется сферическая волна. На пути волны поставлена
преграда с двумя точечными отверстиями s1 и s2, расположенными симметрично по отношению к источнику S.
Отверстия s1 и s2 становятся, согласно принципу Гюйгенса, |
|
|
|||
самостоятельными |
источниками |
колебаний, |
причем |
|
|
колеблющимися с одинаковой частотой и в одинаковых фазах. |
|
|
|||
Справа от преграды будут распространяться две сферические |
|
|
|||
когерентные между собой волны, которые накладываясь друг на |
|
|
|||
Рис. 2.1 |
|
||||
друга, и дают интерференционную картину. Выделим в |
|
||||
|
|
||||
пространстве наложения волн точку С, отстоящую от источников |
|
|
|||
s1 и s2 на расстоянии r1 и r2. Колебания источников можно представить в виде: |
|||||
|
ξ(0, t) = А0 cos(ωt + φ0), |
|
(2.1) |
||
а колебания, дошедшие до точки С, выразятся:
9
( r1 , t ) |
A0 |
cos( t kr1 |
0 ) |
A1 cos( t kr1 |
0 ), |
(2.2) |
|
||||||
|
r1 |
|
|
|
|
|
( r2 , t ) |
|
A0 |
cos( t kr 2 |
0 ) |
A 2 cos( t kr 2 |
0 ). |
|
|
|
(2.3) |
|||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разность фаз слагаемых колебаний в точке С будет |
|
|
|
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
t kr |
|
|
|
t kr |
|
|
|
k ( r |
|
r |
) |
|
( r |
|
r |
). (2.4) |
|||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 |
|
|
2 |
|
|
1 |
|
0 |
|
2 |
|
0 |
|
2 |
1 |
|
|
2 |
1 |
|
||
Если |
|
2 m ( m 1,2 ,3 ....), то волны в точку С приходят в одинаковой фазе. В |
|||||||||||||||||||||
этом случае в точке С будет наблюдаться максимум интерференции, то есть А = А1 + А2.
Так как |
2 |
( r |
|
r ) |
2 m |
, |
то |
r |
2 |
r |
m (условие максимума выражено через |
|
|
||||||||||
|
|
|
2 |
1 |
|
|
|
|
|
|
|
геометрическую разность хода волн). Максимумы интерференции наблюдаются в тех точках, для которых геометрическая разность хода равна целому числу длин волн.
Минимумы наблюдаются для точек, в которые волны приходят
противоположными |
по |
фазе, то есть если ( 2 m 1) . В этом случае |
|
r2 r1 ( 2 m 1) |
|
– |
разность хода равна нечетному числу полуволн. |
|
2 |
|
|
2.2. Стоячие волны
Стоячей волной называют волну, образующуюся при наложении двух встречных когерентных волн. Рассмотрим случай наложения двух плоских волн,
распространяющихся вдоль оси Ох в положительном ξ1(х, t) и отрицательном ξ2(х, t) направлениях:
ξ1(х, t) = А cos(ωt - kx), ξ2(х, t) = А cos(ωt + kx). |
(2.5) |
Для уравнения стоячей волны в соответствии с формулой сложения колебаний можно записать:
ξст(х, t) = ξ1 + ξ2 = 2А cos kx cos ωt |
(2.6) |
Из формулы (2.6) следует, что амплитуда стоячей волны |
|
Аст = | 2А cos kx | |
(2.7) |
зависит от координаты х выбранной точки пространства, изменяясь от минимального значения, равного нулю (Аст = 0), до максимального значения, равного 2А (Аст = 2А).
Найдем координаты точек пространства хп, в которых наблюдается максимальная амплитуда колебаний частиц среды, их называют пучностями стоячей волны, и координаты узлов стоячей волны (ху), для них амплитуда колебаний частиц среды равна нулю:
Аст = 2А cos kxп = ± 1 |
|
2 |
хп = nπ |
хп = |
n, n 0,1,2... |
(2.8) |
|||||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Аст = 0 cos kxу = 0 |
|
2 |
х |
у |
|
n |
ху |
|
|
(n |
1), n 0,1,2... |
(2.9) |
|||
|
|
2 |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
10
