
3 семестр ЭКТ / Физика. Оптика / Методические материалы и лекции / лекции по физике
.pdf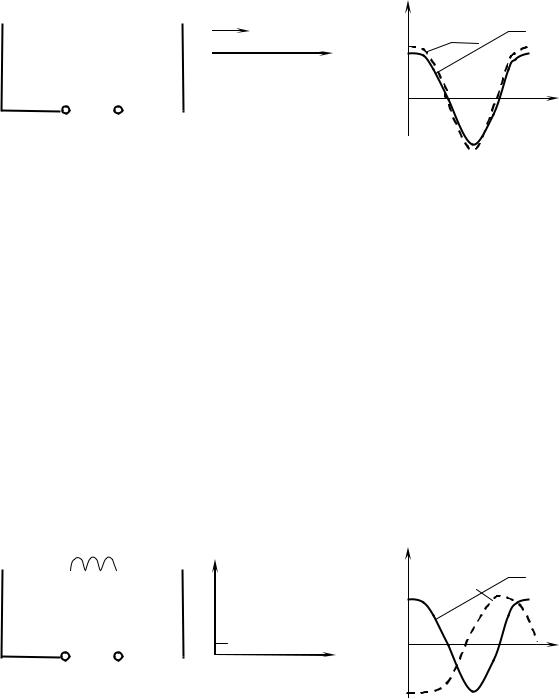
|
R |
Im |
UR |
, I |
|
|||||||||
|
|
|
|
|
|
|
|
|
Um R Im |
I |
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UR |
|
U |
|
|
|
|
|
|
0 |
t |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
Рис. 27. Резистор в це- |
Рис. 28. Вектор- |
Рис. 29. Графики UR (t) и |
||||||||||||
пи переменного тока |
ная диаграмма |
I (t) для цепи содержащей |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
только резистор |
Ток через резистор |
|
Um |
|
|
|
|
|
|
||||||
|
|
|
I |
U |
|
cos t Im cos t. |
|
(77) |
||||||
R |
|
|
||||||||||||
|
|
|
|
|
|
|
R |
|
|
|
||||
Амплитуда силы тока |
|
|
|
Um |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Im |
. |
|
|
(78) |
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
На рис. 28 дана векторная диаграмма амплитудных значений силы тока Im и напряжения Um на резисторе (сдвиг фаз между Im и Um равен нулю).
На рис. 29 приведён график напряжения и тока в цепи, содержащей только резистор.
2. Переменный ток, текущий через катушку индуктивностью L
(R 0, C 0) (рис. 30).
|
|
L |
|
|
UL |
, I |
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
UL L Im |
|
|
|
I |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
UL |
||
|
|
U |
|
Im |
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
t |
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
Рис. 30. Резистор в це- |
Рис. 31. Вектор- |
Рис. 32. Графики UL (t) и |
|||||||||
пи переменного тока |
ная диаграмма |
I (t) для цепи содержащей |
|||||||||
только катушку
Если в цепи приложено переменное напряжение
U Um cos t ,
41

то в ней потечет переменный ток, в результате чего возникнет э.д.с. са-
моиндукции S L dI . dt
Тогда закон Ома
I R ( 1 2 ) 12
для рассматриваемого участка цепи (U s ) имеет вид
Um cos t L |
dI |
0 |
L |
dI |
Um cos t. |
(79) |
|
|
|||||
|
dt |
|
dt |
|
||
Так как внешнее напряжение приложено к катушке индуктивности,
то
UL |
L |
dI |
, |
(80) |
|
||||
|
|
dt |
|
|
это и есть падение напряжения на катушке.
Из уравнения (79) следует, что dI (Um / L)cos tdt ; после интегрирования, учитывая, что постоянная интегрирования равна нулю (так как отсутствует постоянная составляющая тока), получим
|
U |
m |
|
U |
m |
|
|
|
|
|
|
|
|
||
I |
|
sin t |
|
cos |
t |
|
|
Im cos |
t |
|
|
, |
(81) |
||
|
|
L |
2 |
2 |
|||||||||||
|
L |
|
|
|
|
|
|
|
|
||||||
где Im= Um /( ∙L) – амплитудное значение силы тока. Величина
RL L |
(82) |
называется реактивным индуктивным сопротивлением (или индуктивным сопротивлением). Из выражения (82) вытекает, что для постоянного тока ( = 0) катушка индуктивности не имеет сопротивления. Подстановка значения Um = ∙L∙Im в выражение (79) с учетом (80) приводит к следующему значению падения напряжения на катушке индуктивности:
UL LIm cos t. |
(83) |
Сравнение выражений (81) и (83) приводит к выводу, что падение напряжения UL опережает по фазе ток I, текущий через катушку, на /2, что и показано на векторной диаграмме (рис. 31).
На рис. 32 приведены графики напряжения и тока в цепи, содержащей только катушку.
3. Переменный ток, текущий через конденсатор емкостью С
(R 0, L 0) (рис. 33). Если переменное напряжение (76) приложено к конденсатору, то он все время перезаряжается, и в цепи течет переменный ток. Так как все внешнее напряжение приложено к конденсатору, а сопротивлением подводящих проводов можно пренебречь, то
42
Сила тока |
Uc q c Um cos t. |
|
|
|
|
|
(84) |
|||||||||
dq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
I |
|
C Um sin t |
Im cos |
t |
|
|
, |
(85) |
||||||||
dt |
2 |
|||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Um |
|
|
|
|
|
|
|
|||
|
|
I |
|
CU |
|
|
. |
|
|
|
|
|
(86) |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
m |
|
m |
1 |
|
|
|
|
|
|
|
|
||
Величина |
|
|
|
|
|
|
C |
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
R |
|
|
|
|
|
|
|
(87) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
c |
|
C |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
называется реактивным емкостным сопротивлением (или емкостным сопротивлением).
|
С |
|
|
|
|
Im |
UL , I |
|
|
||
|
|
|
|
|
|
|
|
|
I |
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
UC |
|
|
U |
|
|
|
|
|
|
||||
|
1 |
|
|
||||||||
|
|
|
|
|
|||||||
|
|
|
|
|
UC |
|
Im |
0 |
|
t |
|
|
C |
||||||||||
|
|
||||||||||
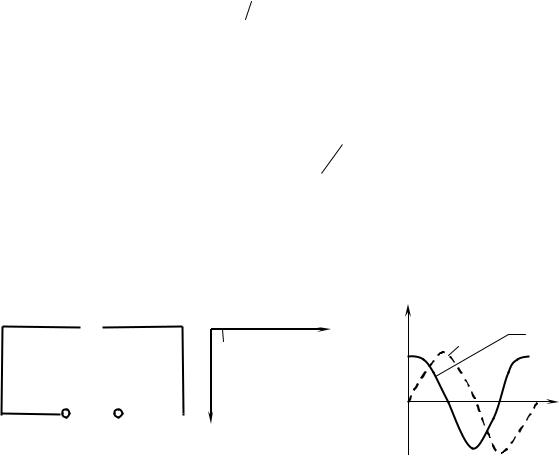
Рис. 33. Конденсатор в |
|
Рис. 34. Вектор- |
Рис. 35. Графики UC (t) и |
||||||||
цепи переменного тока |
|
|
ная диаграмма |
I (t) для цепи содержащей |
|||||||
только конденсатор
Для постоянного тока ( = 0) RС = , то есть постоянный ток через конденсатор течь не может. Падение напряжения на конденсаторе
U |
|
|
1 |
I |
|
cos t. |
(88) |
|
c |
C |
m |
||||||
|
|
|
|
|
Сравнение выражений (85) и (88) приводит к выводу, что падение напряжения UС отстает по фазе от текущего через конденсатор тока I на/2. Это показано на векторной диаграмме (рис. 34).
На рисунке 35 приведены графики напряжения и тока в цепи, содержащий только конденсатор.
Ниже (таблица 4) приведены зависимости сопротивлений в цепи переменного тока от частоты.
В таблице 4: – удельное сопротивление проводника; – его длина; S – площадь поперечного сечения; L – индуктивность катушки; С – электроемкость конденсатора.
43

Таблица 4
Зависимость сопротивлений в цепи переменного тока от частоты
Активное сопротивление |
|
Реактивное |
индуктивное |
Реактивное |
ёмкостное |
|||||||
|
|
|
|
|
|
сопротивление |
сопротивление |
|||||
|
R |
|
|
|
|
RL L |
|
R |
1 |
|
||
|
|
|
|
|
|
|
|
|||||
|
|
S |
|
|
|
C |
C |
|||||
R |
|
|
RL |
|
|
|||||||
|
|
RC |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Цепь переменного тока, содержащая последовательно включенные резистор, катушку индуктивности и конденсатор.
Участок цепи, содержащий резистор сопротивлением R, катушку индуктивностью L и конденсатор емкостью С, к концам которого приложено переменное напряжение (76) представлен на рис. 36, а.
В цепи возникнет переменный ток, который вызовет на всех элементах цепи соответствующие падения напряжения UR, UL и UC. Сумма мгновенных значений падений напряжений на элементах цепи
UR UL UC U ,
где UR ,UL ,UC – соответствующие падения напряжений на сопротивлении, катушке индуктивности и конденсаторе.
На рис. 36, б представлена векторная диаграмма амплитуд падений напряжений на резисторе (UR), катушке (UL) и конденсаторе (UC). Амплитуда Um приложенного напряжения должна быть равна векторной сумме амплитуд всех этих падений напряжений. Как видно из рис. 36, б, угол определяет разность фаз между напряжением и силой тока. Из рисунка 36, б следует, что
tg L 1 C . R
C . R
Из прямоугольного треугольника получаем
|
2 |
|
|
1 |
2 |
2 |
|
(R Im ) |
|
|
( L |
|
) Im |
Um |
, |
|
C |
||||||
|
|
|
|
|
|
|
откуда амплитуда силы тока имеет значение силы тока
Im |
|
|
|
|
Um |
|
|
|
. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|||||
|
|
R |
2 |
|
L |
1 2 |
|||
|
|
|
|
|
|
||||
|
|
||||||||
|
|
|
|
|
|
C |
|||
(91) – закон Ома для цепи переменного тока.
(89)
(90)
(91)
44
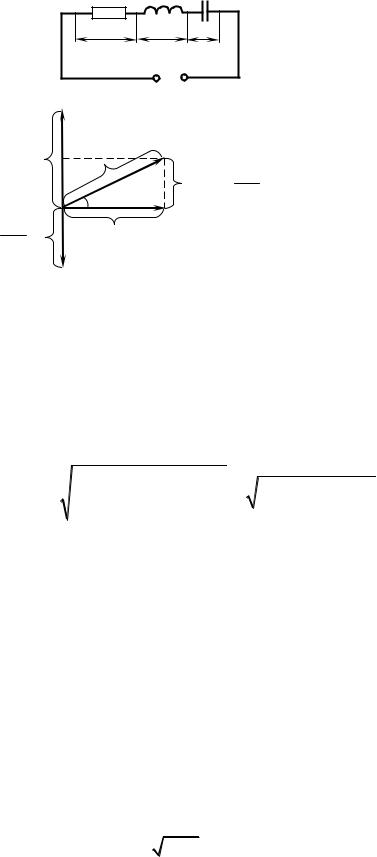
а) |
|
R |
L |
C |
|
|
|
|
|
|
|
|
|
UR |
UL |
UC |
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
UL |
|
|
|
|
LIm |
Um |
U |
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
L |
Im |
|
|
|
C |
||
1 |
|
|
UR |
|
|
С Im |
|
RIm |
|
|
|
UC |
|
|
|
||
|
б) |
|
|
|
|
|
|
|
|
|
|
Рис. 36. К цепи переменного тока, содержащего последовательно включённые резистор, катушку индуктивности и конденсатор
Сила тока в цепи |
I Im cos t . |
|
|
|
|
|
|
(92) |
||||
|
|
|
|
|
|
|
||||||
Сдвиг по фазе между током I |
и приложенным напряжением U |
|||||||||||
определяется формулой (89). |
|
|
|
|
|
|
|
|
|
|
|
|
Полное сопротивление цепи |
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 L |
|
1 2 |
|
|
|
|
|
|
|||
Z |
|
|
|
R2 R R |
2 |
. |
(93) |
|||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
L C |
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|||
Реактивное сопротивление |
|
|
|
|
|
1 |
|
|
|
|
||
|
X R |
R |
L |
, |
|
|
(94) |
|||||
|
|
|
|
|||||||||
|
L |
C |
|
|
|
C |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
где R – реактивное сопротивление; RL – реактивное индуктивное сопротивление; RC – реактивное ёмкостное сопротивление.
1.14. Резонанс напряжений
Если в цепи переменного тока, содержащей последовательно включенные конденсатор, катушку индуктивности и резистор (рис. 36),
L 1/ ( C), (95)
то угол сдвига фаз между током и напряжением (89) обращается в нуль ( = 0), то есть изменения тока и напряжения происходят синфазно. Условию (95) удовлетворяет частота
ωрез 1/ |
L C. |
(96) |
45
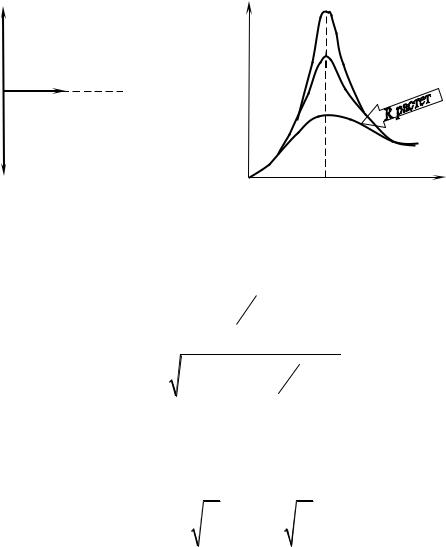
В данном случае полное сопротивление цепи Z (93) становится минимальным, равным активному сопротивлению R цепи, и ток в цепи определяется этим сопротивлением, принимая максимальные (возможные при данном Um) значения. При этом падение напряжения на активном сопротивлении равно внешнему напряжению, приложенному к цепи (UR = U), а падения напряжений на конденсаторе (UC) и катушке индуктивности (UL) одинаковы по амплитуде и противоположны по фазе. Это явление называется резонансом напряжений (последовательным резонансом), а частота (96) – резонансной частотой. Векторная диаграмма для резонанса напряжений приведена на рис. 37, а зависимость амплитуды силы тока от на рис. 38.
LIm |
Im |
Um
RIm
|
1 |
I |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
C |
|
|
|
|
|
|
рез = о |
|
|||||||
Рис. 37. Векторная диаграмма |
|
|
|
Рис. 38. Зависимость амплитуды |
|||||||||||
для резонанса напряжений |
|
|
|
|
силы тока от ω |
|
|||||||||
Таким образом, условие наблюдения резонанса ( RL RC ) |
|
||||||||||||||
|
|
|
|
|
|
|
L |
1 |
|
|
|
|
|
||
|
|
|
1 |
tg |
|
|
|
C |
0, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
R |
|
|
|
|
|
|||
|
L |
|
: |
|
|
|
|
|
. |
(97) |
|||||
C |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
R2 L 1 |
|
|
2 |
R |
|
||||
|
|
|
|
|
Z |
|
C |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В случае резонанса напряжений |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
UL рез |
(UC )рез , |
|
|
|
|
(98) |
||||
подставив в эту формулу значения резонансной частоты и амплитуды напряжений на катушке индуктивности и конденсаторе, получим
UL рез (UC )рез |
|
L |
Im |
|
1 |
|
L |
Um Q Um , (99) |
C |
R |
|
||||||
|
|
|
|
|
C |
|||
где Q – добротность контура, определяемая выражением (71). Так как добротность обычных колебательных контуров больше единицы, то напряжение, как на катушке индуктивности, так и на конденсаторе пре-
46
вышает напряжение, приложенное к цепи. Поэтому явление резонанса напряжений используется в технике для усиления колебания напряжения какой-либо определенной частоты. Например, в случае резонанса на конденсаторе можно получить напряжение с амплитудой Q∙Um (Q в данном случае – добротность контура, которая может быть значительно больше Um). Это усиление напряжения возможно только для узкого интервала частот вблизи резонансной частоты контура, что позволяет выделить из многих сигналов одно колебание определенной частоты, то есть на радиоприёмнике настроиться на нужную длину волны. Явление резонанса напряжений необходимо учитывать при расчете изоляции электрических линий, содержащих конденсаторы и катушки индуктивности, так как иначе может наблюдаться их пробой.
1.15. Резонанс токов (параллельный резонанс)
Рассмотрим цепь переменного тока, содержащую параллельно включенные конденсатор емкостью С и катушку индуктивностью L
(рис. 39).
Для простоты допустим, что активное сопротивление обеих ветвей настолько мало, что им можно пренебречь. Если приложенное напряжение изменяется по закону U = Umсos t, то, согласно формуле (92), в ветви 1С2 течет ток
I1 Im1 cos t 1 , |
(100) |
амплитуда которого определяется из выражения (91) при условии R = 0
и L= 0:
|
Im |
|
|
Um |
. |
(101) |
|||
|
1 |
|
|
|
|||||
1 |
|
|
|
|
|
|
|||
|
|
C |
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
I1 |
|
C |
|
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
I2 |
|
L |
|
|
||||
U
Рис. 39. Цепь переменного тока
47

Начальная фаза 1 этого тока по формуле (89) определяется равенством
tg 1 , |
1 |
|
2n |
3 |
|
,n 1,2,3 |
|
|
|
|
|
(102) |
|||||
2 |
||||||||
|
|
|
|
|
|
|
Аналогично, сила тока в ветви 1L2
I2 |
Im |
cos t 2 , |
(103) |
|
2 |
|
|
амплитуда которого определяется при условии R = 0 и С = (условие отсутствия емкости в цепи):
|
Im |
|
Um |
. |
|
|
|
|
(104) |
||
|
|
|
|
|
|
||||||
|
|
2 |
|
L |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
Начальная фаза 2 этого тока |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
tg 2 , |
tg 2 |
2n |
|
|
, |
n 1,2,3 |
(105) |
||||
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
Из сравнения выражений (102) и (105) вытекает, что разность фаз токов в ветвях 1С2 и 1L2 равна 1 – 2 = , то есть токи в ветвях противоположны по фазе. Амплитуда силы тока во внешней (неразветвленной) цепи
|
|
|
Im |
|
Im |
Im |
|
Um |
C |
1 |
|
. |
(106) |
||||
|
|
|
|||||||||||||||
|
|
|
L |
||||||||||||||
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
||
|
|
|
1 |
|
, то Im |
Im |
|
|
|
|
|||||||
Если рез |
|
|
|
и Im 0. |
|
||||||||||||
|
|
|
|
||||||||||||||
LC |
|
||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно включенные конденсатор и катушку индуктивности, при приближении частоты приложенного напряжения к резонансной частоте рез называется резонансом то-
ков (параллельным резонансом). В данном случае для резонансной частоты получили такое же значение, как и при резонансе напряжений.
Амплитуда силы тока Im оказалась равна нулю потому, что активным сопротивлением контура пренебрегли. Если учесть сопротивление R, то разность фаз 1 – 2 будет равна , поэтому при резонансе токов амплитуда силы тока Im будет отлична от нуля, но примет наименьшее возможное значение. Таким образом, при резонансе токов во внешней цепи токи I1 и I2 компенсируются, и сила тока I в подводящих проводах достигает минимального значения, обусловленного только током через резистор. При резонансе токов силы токов I1 и I2 могут значительно превышать силу тока I.
Рассмотренный контур оказывает большое сопротивление переменному току с частотой, близкой к резонансной. Поэтому это свойство
48
резонанса токов используется в резонансных усилителях, позволяющих выделять одно определенное колебание из сигнала сложной формы. Кроме того, резонанс токов используется в индукционных печах, где нагревание металлов производится вихревыми токами. В них ёмкость конденсатора, включенного параллельно нагревательной катушке, подбирается так, чтобы при частоте генератора получился резонанс токов, в результате чего сила тока через нагревательную катушку будет гораздо больше, чем сила тока в подводящих проводах.
1.16. Мощность, выделяемая в цепи переменного тока
Мгновенное значение мощности P t U t I t – определяется произведением мгновенных значений напряжения и тока.
P t ImUm cos t cos t ImUm cos2 t cos sin t cos t sin , (107)
здесь U Um cos t ; I Im cos t .
Практический интерес представляет не мгновенное значение мощности, а ее среднее значение за период колебания. Учитывая, что
cos2 t = 1/2, sin tcos t = 0, получим
P |
1 |
|
I |
|
U |
|
cos . |
(108) |
|||||
|
|
|
|
m |
m |
||||||||
2 |
|
|
|
|
|
|
|||||||
Из векторной диаграммы (рис. 36) следует, что |
|
||||||||||||
Um сos = R∙Im. |
(109) |
||||||||||||
Поэтому |
|
|
|
|
|
||||||||
P |
1 |
R Im2 . |
|
(110) |
|||||||||
|
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|||||||
Такую же мощность развивает постоянный ток |
|
||||||||||||
I |
I |
m |
|
. |
|
|
|
|
(111) |
||||
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
||||
Практический интерес представляет именно средняя мощность за период колебания. Записанную формулу для средней мощности можно получить и так
|
|
1 |
T |
P t dt |
1 |
T |
Im Um cos t cos t dt |
1 |
|
|
|||||||
P |
|
|
0 |
|
0 |
|
Im |
Um cos . |
|||||||||
T |
T |
2 |
|||||||||||||||
Величины |
|
|
|
I |
|
|
|
U |
|
|
|
|
|
||||
|
|
|
|
|
|
I |
m |
|
; U |
m |
|
|
|
(112) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|||||
называются соответственно действующими (или эффективными) значениями тока и напряжения.
49
Все амперметры и вольтметры градуируются по действующим значениям тока и напряжения.
Учитывая действующие значения тока и напряжения, выражение средней мощности (108) можно записать в виде
P IU cos , |
(113) |
где множитель соs называется коэффициентом мощности. Коэффициент мощности (из векторной диаграммы, рис. 36)
cos |
|
|
|
|
R |
|
|
|
. |
(114) |
|
|
|
|
|
|
|
||||
|
|
R |
2 |
|
L |
1 2 |
|
|||
|
|
|
|
|
|
|
||||
|
|
|
||||||||
|
|
|
|
|
|
C |
|
|||
Мощность, выделяемая в цепи переменного тока, в общем случае зависит не только от силы тока и напряжения, но и от сдвига фаз между ними. Если в цепи реактивное сопротивление отсутствует, то cos 1 и P I U . Если цепь содержит только реактивное сопротивление (R = 0), то cos 0 и средняя мощность равна нулю, какими бы большими ни были ток и напряжение. Если cos имеет значения, существенно меньшие единицы, то для передачи заданной мощности при данном напряжении генератора нужно увеличивать силу тока I, что приведет либо к выделению джоулевой теплоты, либо потребует увеличения сечения проводов, что повышает стоимость линий электропередачи. Поэтому на практике всегда стремятся увеличить соs , наименьшее допустимое значение которого для промышленных установок составляет примерно
0,85.
50
