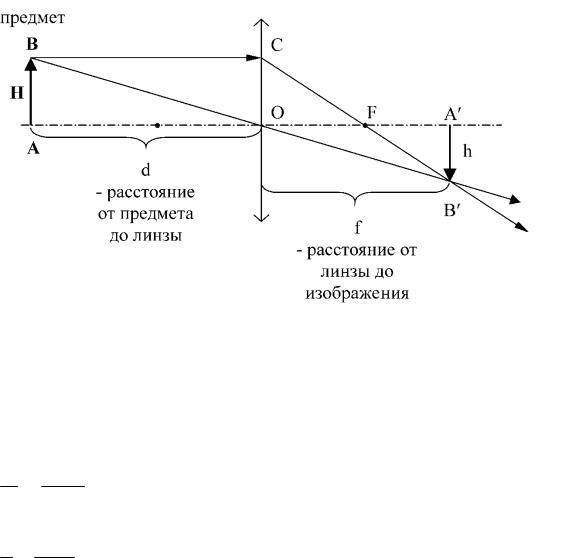
§ 5. ФОРМУЛА ТОНКОЙ ЛИНЗЫ

Формула тонкой линзы дает связь между величинами, определяющими положение предмета и изображения относительно тонкой линзы.

DABO (рис. 9.9) подобен A′B′O , значит: f = h .

d H

Рис. 9.9

DOCF подобен A′B′F , значит: h = f − F ,

H F

следовательно: f = f − F ,

d F

освободимся от знаменателя:

f × F = d × f − d × F,

поделим на dfF, тогда:

откуда следует формула тонкой линзы:

Если предмет и изображение находятся по разные стороны линзы, то d > 0, f > 0 (см. рис. 9.7, а и 9.9), если по одну сторону от линзы, то d > 0, f < 0 (рис. 9.7, б и 9.8). Правило знаков для F приведено в § 3:

F> 0 – для собирающей линзы:

F< 0 – для рассеивающей линзы.

Из рис. 9.9 можно найти линейное увеличение в линзе.

Линейным увеличением Г называется отношение размеров изображения к размерам предмета, перпендикулярного к оптической оси. Из рис. 9.9 линейное увеличение равно:

Линейное увеличение равно отношению расстояния f от изображения до линзы к расстоянию d от предмета до линзы.

ИТОГИ ЛЕКЦИИ № 9

1.Линзой называется прозрачное тело, ограниченное двумя, чаще всего сферическими, поверхностями. По оптическим свойствам линзы делятся на собирающие и рассеивающие.

2.Линза называется тонкой, если ее толщина намного меньше, чем

радиусы кривизны R1 и R 2 обеих поверхностей. На чертежах тонкая линза изображается в виде преломляющей поверхности.

3.Главной оптической осью линзы называется прямая, проходящая через центры кривизны обеих поверхностей линзы.

4.Оптическим центром линзы называется точка пересечения главной оптической оси с преломляющей плоскостью линзы.

5.Фокусом линзы называется точка, в которой сходятся лучи, параллельные оптической оси.

6.Фокусное расстояние тонкой линзы связано с радиусами кривизны преломляющих поверхностей формулой, справедливой для параксиальных (приосевых) лучей:

R> 0 – для выпуклой поверхности, R< 0 – для вогнутой поверхности. n л и n ср – показатели преломления линзы и среды.

7. Оптической силой Ф линзы (9.2) называется величина, обратная фокусному расстоянию:

Ф ≡ 1 / F.

8.Изображение точки находится на пересечении двух лучей. Луч, параллельный оптической оси, преломляясь, идет через фокус. Луч, проходящий через оптический центр, идет, не преломляясь. Их пересечение позволяет найти положение изображения точки.

9.Формула тонкой линзы имеет вид (9.3):

1 + 1 = 1 , d f F

где d – расстояние от предмета до линзы; f – расстояние от линзы до изображения; F – фокусное расстояние линзы.

ЛЕКЦИЯ № 10

Интерференция света

Интерференция от двух монохроматических источников одинаковой частоты. Когерентность. Условия максимума и минимума на разность фаз. Оптическая разность хода. Расчет интерференционной картины от двух источников. Способы получения когерентных источников

Интерференцией волн называется наложение волн друг на друга, при котором происходит устойчивое перераспределение энергии в пространстве, вследствие чего образуется так называемая интерференционная картина (от лат. Inter – взаимно, ferio – ударяю). Интерференционная картина световых волн представляет собой чередование темных и светлых участков экрана.

Интерференция – это одно из основных свойств волн любой природы: упругих, электромагнитных, в том числе и световых. Интерференция наблюдается только от когерентных источников.

§ 1. ИНТЕРФЕРЕНЦИЯ ОТ ДВУХ МОНОХРОМАТИЧЕСКИХ ИСТОЧНИКОВ ОДИНАКОВОЙ ЧАСТОТЫ

Изобразим два точечных источника S1 и S2, излучающих монохроматические световые волны одинаковой частоты ω. Проанализируем, от чего зависит интенсивность света в точке пространства, удаленной от первого

E1 (r1 , t) = E1m cos(ωt − k1 r1 + α1);

E2 (r2 , t) = E2m cos(ωt − k 2 r2 + α2).

Амплитуда результирующего колебания при сложении колебаний одинаковой частоты и одинакового направления была найдена в лекции № 2 (см

(2.2)).

Обозначим через δ = (− k1r1 + α1 ) − (− k 2 r2 + α 2 ) – разность фаз колебаний, возбуждаемых в точке наблюдения источниками S1 и S2, тогда:

E 2 = E12 + E 22 + 2E1E 2 cos δ .

Интенсивность найдем, усреднив это выражение по времени (см. (7.9)):