
- •ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- •ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- •ФИЗИКА КОЛЕБАНИЙ
- •ЛЕКЦИЯ № 1
- •§ 1. ПОНЯТИЕ О КОЛЕБАТЕЛЬНЫХ ПРОЦЕССАХ
- •§ 2. УПРУГИЕ И КВАЗИУПРУГИЕ СИЛЫ
- •§ 3. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- •§ 4. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР. ЭНЕРГИЯ КОЛЕБАНИЙ ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА
- •ИТОГИ ЛЕКЦИИ № 1
- •ЛЕКЦИЯ № 2
- •§ 1. ВЕКТОРНАЯ ДИАГРАММА КОЛЕБАНИЯ
- •§ 2. СЛОЖЕНИЕ КОЛЕБАНИЙ ОДИНАКОВОЙ ЧАСТОТЫ И ОДИНАКОВОГО НАПРАВЛЕНИЯ
- •§ 3. СЛОЖЕНИЕ КОЛЕБАНИЙ ОДНОГО НАПРАВЛЕНИЯ И БЛИЗКИХ ЧАСТОТ
- •§ 4. СЛОЖЕНИЕ ВЗАИМНО-ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ
- •ИТОГИ ЛЕКЦИИ № 2
- •ЛЕКЦИЯ № 3
- •§ 1. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
- •§ 2. ПЕРИОД ЗАТУХАЮЩИХ КОЛЕБАНИЙ
- •§ 3. ЛОГАРИФМИЧЕСКИЙ ДЕКРЕМЕНТ ЗАТУХАНИЯ
- •§ 4. ДОБРОТНОСТЬ
- •ИТОГИ ЛЕКЦИИ № 3
- •ЛЕКЦИЯ № 4
- •§ 1. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
- •§ 3. РЕЗОНАНС
- •ИТОГИ ЛЕКЦИИ № 4
- •ВОЛНЫ
- •ЛЕКЦИЯ № 5
- •§ 1. УПРУГАЯ ВОЛНА
- •§ 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ ДЛЯ ВОЛНОВОГО ПРОЦЕССА
- •§ 3. УРАВНЕНИЕ ПЛОСКОЙ ВОЛНЫ
- •§ 4. ФАЗОВАЯ СКОРОСТЬ
- •§ 5. УРАВНЕНИЕ СФЕРИЧЕСКОЙ ВОЛНЫ
- •§ 6. ВОЛНОВОЕ УРАВНЕНИЕ
- •ИТОГИ ЛЕКЦИИ № 5
- •ЛЕКЦИЯ № 6
- •§ 1. ЭНЕРГИЯ УПРУГОЙ ВОЛНЫ
- •§ 2. ПЛОТНОСТЬ ЭНЕРГИИ УПРУГОЙ ВОЛНЫ
- •§ 3. ПЛОТНОСТЬ ПОТОКА ЭНЕРГИИ
- •§ 4. ВЕКТОР УМОВА. ИНТЕНСИВНОСТЬ
- •§ 5. СТОЯЧИЕ ВОЛНЫ
- •§ 6. КОЛЕБАНИЯ СТРУНЫ, ЗАКРЕПЛЕННОЙ С ДВУХ КОНЦОВ
- •ИТОГИ ЛЕКЦИИ № 6
- •ЛЕКЦИЯ № 7
- •§ 1. ПОНЯТИЕ ОБ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЕ
- •§ 2. ПЛОСКАЯ ЭЛЕКТРОМАГНИТНАЯ ВОЛНА
- •§ 3. ЭНЕРГИЯ И ИНТЕНСИВНОСТЬ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
- •§ 4. ИЗЛУЧЕНИЕ ДИПОЛЯ
- •§ 5. ВИБРАТОР ГЕРЦА
- •ИТОГИ ЛЕКЦИИ № 7
- •ВОЛНОВАЯ ОПТИКА
- •ЛЕКЦИЯ № 8
- •§ 1. СВЕТОВЫЕ ВОЛНЫ
- •§ 2. ИНТЕНСИВНОСТЬ СВЕТА. СВЕТОВОЙ ПОТОК
- •§ 3. ОСНОВНЫЕ ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- •§ 4. ПОЛНОЕ ВНУТРЕННЕЕ ОТРАЖЕНИЕ
- •ИТОГИ ЛЕКЦИИ № 8
- •ЛЕКЦИЯ № 9
- •§ 1. СОБИРАЮЩИЕ И РАССЕИВАЮЩИЕ ЛИНЗЫ
- •§ 2. ФОКУСЫ ЛИНЗЫ, ФОКАЛЬНАЯ ПЛОСКОСТЬ
- •§ 3. ФОКУСНОЕ РАССТОЯНИЕ ТОНКОЙ ЛИНЗЫ
- •§ 4. ПОСТРОЕНИЕ ИЗОБРАЖЕНИЯ В ЛИНЗАХ
- •§ 5. ФОРМУЛА ТОНКОЙ ЛИНЗЫ
- •ИТОГИ ЛЕКЦИИ № 9
- •ЛЕКЦИЯ № 10
- •§ 1. ИНТЕРФЕРЕНЦИЯ ОТ ДВУХ МОНОХРОМАТИЧЕСКИХ ИСТОЧНИКОВ ОДИНАКОВОЙ ЧАСТОТЫ
- •§ 2. КОГЕРЕНТНОСТЬ
- •§ 4. ОПТИЧЕСКАЯ РАЗНОСТЬ ХОДА
- •§ 5. РАСЧЕТ ИНТЕРФЕРЕНЦИОННОЙ КАРТИНЫ ОТ ДВУХ ИСТОЧНИКОВ
- •§ 6. СПОСОБЫ ПОЛУЧЕНИЯ КОГЕРЕНТНЫХ ИСТОЧНИКОВ
- •ИТОГИ ЛЕКЦИИ № 10
- •ЛЕКЦИЯ № 11
- •§ 1. ИНТЕРФЕРЕНЦИЯ ПРИ ОТРАЖЕНИИ ОТ ПРОЗРАЧНЫХ ПЛАСТИНОК
- •§ 2. КОЛЬЦА НЬЮТОНА
- •§ 3. ПРОСВЕТЛЕННАЯ ОПТИКА
- •§ 4. ИНТЕРФЕРОМЕТРЫ
- •ИТОГИ ЛЕКЦИИ № 11
- •ЛЕКЦИЯ № 12
- •§ 1. ЯВЛЕНИЕ ДИФРАКЦИИ ВОЛН
- •§ 2. ПРИНЦИП ГЮЙГЕНСА – ФРЕНЕЛЯ
- •§ 3. ЗОНЫ ФРЕНЕЛЯ
- •§ 4. ДИФРАКЦИЯ ФРЕНЕЛЯ НА КРУГЛОМ ОТВЕРСТИИ
- •ИТОГИ ЛЕКЦИИ № 12
- •ЛЕКЦИЯ № 13
- •§ 1. ДИФРАКЦИЯ НА ДИФРАКЦИОННОЙ РЕШЕТКЕ
- •§ 2. ДИФРАКЦИОННАЯ РЕШЕТКА КАК СПЕКТРАЛЬНЫЙ ПРИБОР
- •§ 3. ДИСПЕРСИЯ ДИФРАКЦИОННОЙ РЕШЕТКИ
- •§ 4. РАЗРЕШАЮЩАЯ СИЛА ДИФРАКЦИОННОЙ РЕШЕТКИ
- •§ 5. РАЗРЕШАЮЩАЯ СИЛА ОБЪЕКТИВА
- •ИТОГИ ЛЕКЦИИ № 13
- •ЛЕКЦИЯ № 14
- •§ 1. ЕСТЕСТВЕННЫЙ И ПОЛЯРИЗОВАННЫЙ СВЕТ
- •§ 2. ПРИНЦИП ДЕЙСТВИЯ ПОЛЯРИЗАТОРА ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
- •§ 3. ЗАКОН МАЛЮСА
- •§ 4. ПОЛЯРИЗАЦИЯ ПРИ ОТРАЖЕНИИ И ПРЕЛОМЛЕНИИ. ФОРМУЛЫ ФРЕНЕЛЯ
- •§ 5. ЗАКОН БРЮСТЕРА
- •ИТОГИ ЛЕКЦИИ № 14
- •ЛЕКЦИЯ № 15
- •§ 1. СВОЙСТВА ДВОЙНОГО ЛУЧЕПРЕЛОМЛЕНИЯ
- •§ 2. ДВОЙНОЕ ЛУЧЕПРЕЛОМЛЕНИЕ
- •§ 3. ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННЫХ ЛУЧЕЙ
- •§ 4. ИСКУССТВЕННОЕ ДВОЙНОЕ ЛУЧЕПРЕЛОМЛЕНИЕ
- •ИТОГИ ЛЕКЦИИ № 15
- •ЛЕКЦИЯ № 16
- •§ 1. ДИСПЕРСИЯ СВЕТА
- •§ 2. ПОГЛОЩЕНИЕ СВЕТА. ЗАКОН БУГЕРА
- •§ 3. РАССЕЯНИЕ СВЕТА
- •ИТОГИ ЛЕКЦИИ № 16
- •ЛЕКЦИЯ № 17
- •§ 1. СВЯЗЬ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ С ДИПОЛЬНЫМ МОМЕНТОМ МОЛЕКУЛЫ
- •§ 2. СВЯЗЬ ЭЛЕКТРИЧЕСКОГО ДИПОЛЬНОГО МОМЕНТА МОЛЕКУЛЫ С НАПРЯЖЕННОСТЬЮ ПОЛЯ СВЕТОВОЙ ВОЛНЫ
- •§ 3. УРАВНЕНИЕ ДВИЖЕНИЯ ЭЛЕКТРОНА В АТОМЕ ПОД ДЕЙСТВИЕМ СВЕТОВОЙ ВОЛНЫ И ЕГО РЕШЕНИЕ
- •§ 4. ЗАВИСИМОСТЬ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ ОТ ЧАСТОТЫ
- •§ 5. ГРУППОВАЯ И ФАЗОВАЯ СКОРОСТЬ
- •ИТОГИ ЛЕКЦИИ № 17
- •ТЕСТ №6
- •ОТВЕТЫ НА ВОПРОСЫ ТЕСТА №6
- •ТЕСТ № 7
- •ОТВЕТЫ НА ВОПРОСЫ ТЕСТА № 7
- •ТЕСТ № 8
собирающая
рассеивающая
F |
F |
F |
F |
|
|
|
|
а) б)
Рис. 9.3
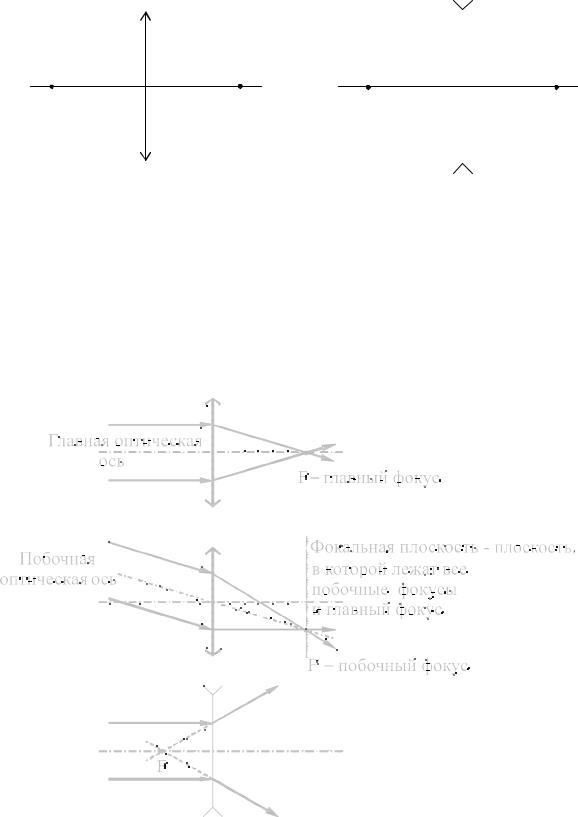
§ 2. ФОКУСЫ ЛИНЗЫ, ФОКАЛЬНАЯ ПЛОСКОСТЬ
На рис. 9.4 буквой F обозначены фокусы линзы – точки, в которых собираются параллельные оптической оси лучи, прошедшие через линзу (или их продолжения).
П |
Рис. 9.4 |
|
Прямая, проходящая через центры кривизны обеих поверхностей линзы,
называется главной оптической осью.
Точка пересечения главной оптической оси с преломляющей плоскостью линзы называется оптическим центром линзы.
Плоскость, проведенная через фокус линзы перпендикулярно к главной оптической оси, называется фокальной плоскостью линзы.
§ 3. ФОКУСНОЕ РАССТОЯНИЕ ТОНКОЙ ЛИНЗЫ
Буквой F обозначают также и фокусное расстояние линзы – расстояние от фокуса до оптического центра линзы (рис. 9.5).
Оптический центр линзы
Главная оптическая ось |
F – фокус |
F – фокусное расстояние
Рис. 9.5
Для сферической тонкой линзы на основе закона преломления получается следующая формула для фокусного расстояния:
F = |
|
|
1 |
|
× |
|
|
1 |
|
. |
(9.1) |
||
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
n л |
|
-1 |
|
1 |
+ |
|
|
||||
|
|
|
|
|
|||||||||
|
|
||||||||||||
|
|
n |
ср |
|
R1 |
|
R 2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь nл и nср – |
показатели преломления линзы и среды, соответственно. |
||||||||||||
R1 и R2 – радиусы кривизны линзы, они – |
величины алгебраические. |
||||||||||||
Эта формула справедлива только для приосевых (параксиальных) лучей. R1, R2 – радиусы кривизны сферических поверхностей линзы, они могут быть положительными и отрицательными. Радиус кривизны выпуклой поверхности линзы считается положительным, вогнутой – отрицательным.
Выбор знаков R1 и R2 в приведенной нами формуле для F иллюстрирует рис. 9.6.
Для собирающей линзы фокусное расстояние F положительно, для рассеивающей – отрицательно. Оптической силой линзы называют величину Ф, обратную фокусному расстоянию линзы:
Φ ≡ |
1 |
, |
(9.2) |
|
|||
|
F |
|
|
Единица оптической силы – диоптрия (дптр). 1 дптр = 1 / м.
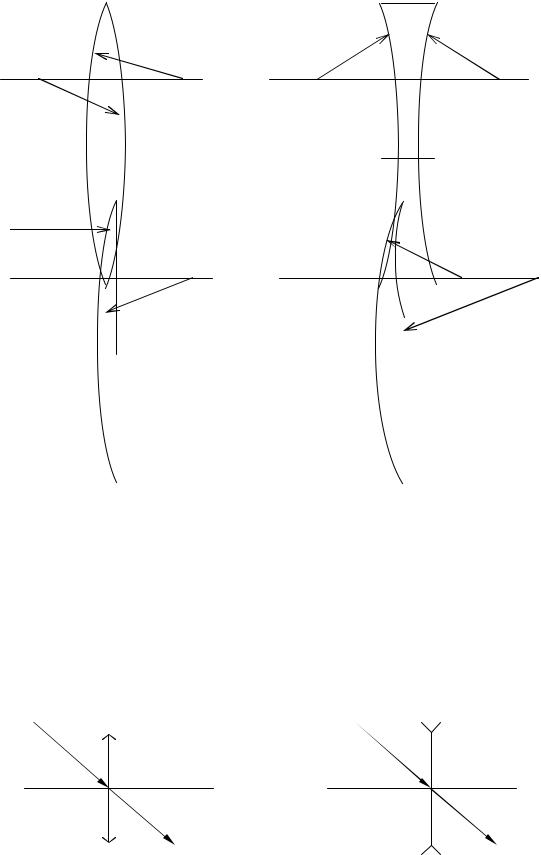
R1 > 0 |
R1 < 0 |
R2 < 0 |
|
|
R2 > 0
R 2 = ∞
|
|
R1 > 0 |
|
R1 |
> 0 |
R2 |
< 0 |
|
|
Рис. 9.6
§ 4. ПОСТРОЕНИЕ ИЗОБРАЖЕНИЯ В ЛИНЗАХ
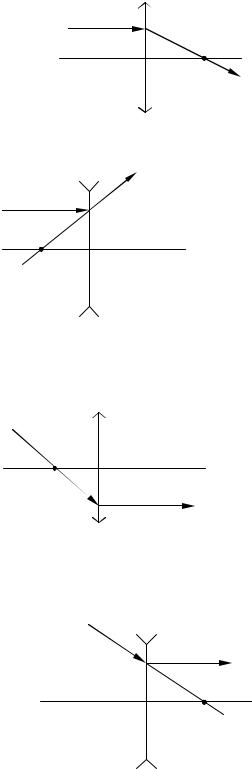
Для построения изображения предмета необходимо построить изображение каждой его точки.
Для построения изображения точки достаточно найти точки пересечения двух любых лучей, идущих из заданной точки.
Удобнее всего использовать в качестве одного из этих лучей луч, идущий через оптический центр, он идет через линзу, не отклоняясь:
Другой удобный луч – это луч, идущий параллельно оптической оси. Он,
преломляясь в линзе, проходит через фокус, если линза собирающая:
F
Оптическая ось
Если линза рассеивающая, то через фокус проходит продолжение луча:
Оптическая ось
F
И, если луч шел через фокус собирающей линзы, то после преломления он пойдет параллельно оптической оси:
F |
Оптическая ось |
Для рассеивающей линзы параллельно оптической оси пойдет после преломления луч, продолжение которого проходит через фокус:
Оптическая ось |
F |
Примеры построения изображения точки в собирающей линзе
приведены на рис. 9.7, а, б.
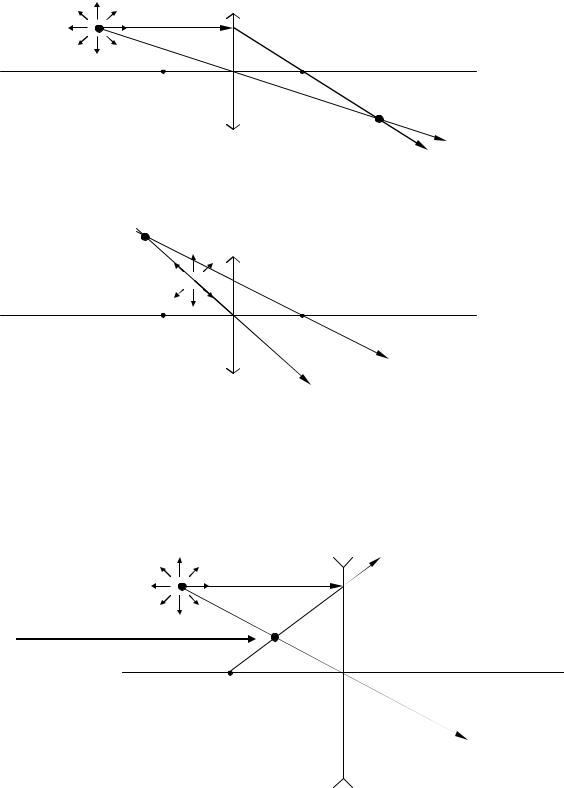
а) Точка дальше фокуса
|
F |
F |
Действительное |
|
изображение точки |
б) Мнимое изображение точки
Точка ближе фокуса 


F
F
Лучи
расходятся
Рис. 9.7
Пример построения изображения точки в рассеивающей линзе дан на рис.
9.8.
Точка
Мнимое изображение точки
F
Рис. 9.8
