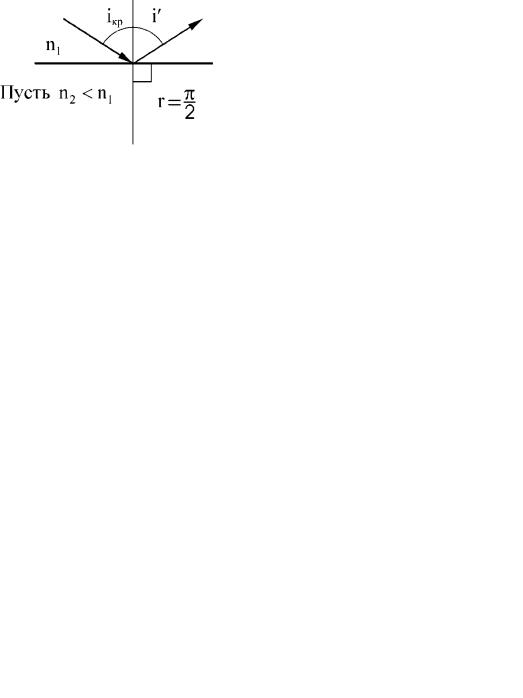
§ 4. ПОЛНОЕ ВНУТРЕННЕЕ ОТРАЖЕНИЕ
Полное внутреннее отражение наблюдается, если свет падает из оптически более плотной среды на границу раздела с оптически менее плотной средой под углом, большим предельного. Найдем предельный угол полного внутреннего отражения. Рассмотрим рис. 8.2. На границе раздела двух сред свет частично отражается, частично преломляется. Воспользуемся законом преломления.
|
|
i |
|
|
|
|
sin i |
= n 2 ® |
sin r = |
n1 |
× sin i , |
|
||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
sin r |
n1 |
|
|
n 2 |
|
|
||||
|
n1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
так как |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
n1 |
> 1, то sin r > sin i, |
|
r > i . |
|
|||||
Пусть n2 < n1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
r > i |
|
n2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
Следовательно, |
если |
свет |
падает |
из |
||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
оптически |
более |
плотной |
среды |
на |
||||||
|
|
|
|
|
|
|||||||||||
|
|
Рис. 8.2 |
|
|
границу |
раздела |
с оптически менее |
|||||||||
|
|
|
|
|
|
плотной средой, то при увеличении угла |
||||||||||
|
|
|
|
|
|
|||||||||||
падения i угол преломления тоже увеличивается. При этом интенсивность отраженного луча растет, а преломленного – падает (их сумма равна
интенсивности падающего луча). При каком-то значении i = iкр угол r = π / 2 ,
интенсивность преломленного луча станет равной нулю, весь свет отразится. При дальнейшем увеличении угла i > iкр преломленного луча не будет,
происходит полное отражение света.
Значение критического угла падения, при котором отражение, найдем, положив в законе преломления значит:
sin iкр = n2 |
, |
|
||
n1 |
|
|
|
|
т. е. |
|
|
|
|
iкр = arcsin |
n 2 |
|
. |
(8.9) |
n1 |
|
|||
|
|
|
|
|
Угол iкр называют также предельным углом внутреннего отражения.
Предельный угол внутреннего отражения изображен на рис. 8.3.
Полное внутреннее отражение находит применение, например, в волоконной оптике. Волоконная оптика позволяет видеть предметы, не расположенные на прямом луче зрения. Для передачи световой энергии используется так называемый световод. Световод – это стержень
начинается полное , тогда sin r = 1 ,
Рис. 8.3
или волокно с большим показателем преломления и малым коэффициентом поглощения. Лучи, вошедшие в световод, отражаются от его стенок и перемещаются к выходу после нескольких полных внутренних отражений. Изгибом световода можно передать световую энергию вбок в любое место. Это позволяет использовать световой сигнал для дальней связи. Главное преимущество использования света для связи заключается в том, что в этом диапазоне может работать без потерь громадное число передатчиков, так как длина световой волны очень мала.
ИТОГИ ЛЕКЦИИ № 8
1.Свет имеет электромагнитную природу. С современной точки зрения, свет обладает корпускулярно-волновым дуализмом.
2.Видимый свет имеет длину волны в интервале 400–760 нм.
Скорость света в вакууме c = 3 ×108 м / с, скорость распространения света в среде, как и любой электромагнитной волны, равна (7.3)
v = |
|
|
|
|
c |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
εμ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
3. Для |
световой волны |
вводятся абсолютный |
показатель |
преломления |
||||||||||
(8.1): |
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
n = |
|
|
|
|
|
|
|
|
|
|
|
|||
v |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и относительный показатель преломления (8.3): |
|
|
||||||||||||
n21 |
= |
|
|
n |
2 . |
|
|
|
|
|
||||
|
|
n1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. Абсолютный показатель преломления зависит от диэлектрической |
||||||||||||||
проницаемости среды: n = |
|
|
(8.2), ε и n |
|
|
|||||||||
|
ε |
зависят |
от частоты |
|||||||||||
электромагнитной волны ν или длины волны λ. Зависимость показателя преломления от длины волны (или частоты) называется дисперсией.
5. В световой волне, как и в любой электромагнитной, векторы E и H колеблются перпендикулярно направлению распространения волны. Т. е. световые волны поперечны.
6. Световой вектор – это вектор напряженности электрического поля E в электромагнитной волне. Уравнение монохроматической световой волны – это
уравнение |
|
E = Em cos(ωt − kr + α) . |
(8.4) |
7. Интенсивность света численно равна средней энергии, переносимой световой волной в единицу времени через единицу поверхности площадки, расположенной перпендикулярно направлению распространения волны. Интенсивность света (8.6) пропорциональна квадрату амплитуды световой волны и показателю преломления:
I ~ nE2m .
8.Световым потоком Ф называется световой поток энергии, оцениваемый по зрительному ощущению.
9.Лучом называется линия, вдоль которой распространяется световая энергия. На понятии луча основана геометрическая оптика.
10.Законы геометрической оптики:
а) Закон прямолинейного распространения света: в однородной среде свет распространяется прямолинейно;
б) Закон независимости световых лучей: при пересечении лучи не возмущают друг друга;
в) На границе раздела двух сред свет частично отражается, частично преломляется Закон отражения: луч падающий, луч отраженный и перпендикуляр к границе раздела лежат в одной плоскости. Угол падения равен углу отражения:
i = i' ; |
(8.7) |
г) Закон |
преломления: луч падающий, луч преломленный и |
перпендикуляр к границе раздела лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления равно относительному показателю преломления:
sini |
= |
n2 |
= n21. |
(8.8) |
|
sinr |
n1 |
||||
|
|
|
11. Если луч падает из оптически более плотной среды с показателем преломления n1 на границу раздела с оптически менее плотной средой с показателем преломления n2 под углом, большим предельного, то наблюдается полное внутреннее отражение. Значение предельного (или критического) угла находится по формуле (8.9):
iкр = arcsin n2 . n1
ЛЕКЦИЯ № 9
Тонкие линзы
Собирающие и рассеивающие линзы. Фокусы линзы. Фокальная плоскость. Фокальное расстояние тонкой линзы. Построение изображения в линзах.
Формула тонкой линзы
§ 1. СОБИРАЮЩИЕ И РАССЕИВАЮЩИЕ ЛИНЗЫ
Линза – это прозрачное тело, ограниченное двумя, чаще всего, сферическими преломляющими поверхностями. Обычно линзы делают стеклянными.
Линзы бывают собирающими и рассеивающими.
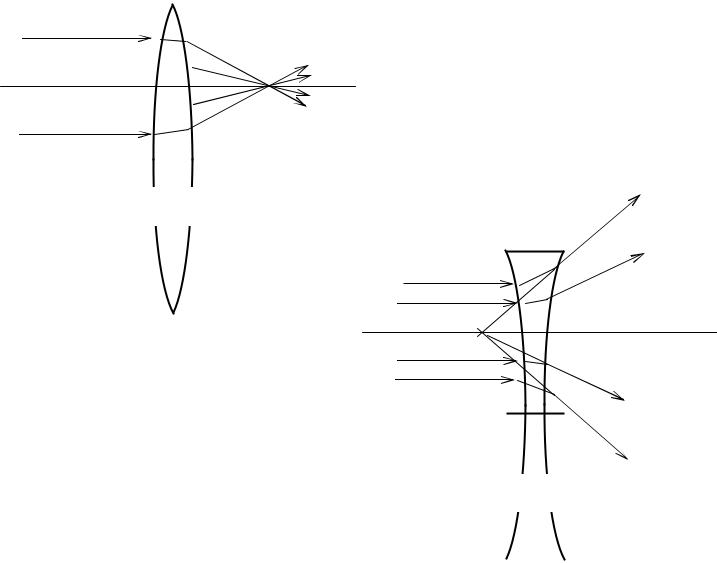
Собирающая линза в средней
F части толще и отклоняет лучи к оптической оси, если показатель 
преломления линзы больше
показателя преломления среды
(рис. 9.1).
Рис. 9.1
Рассеивающая линза в средней части тоньше и отклоняет лучи от оптической оси
(рис. 9.2).
Такой ход лучей в линзах можно объяснить, применяя закон преломления.
Линза называется тонкой, если ее
толщиной можно пренебречь по сравнению с радиусом кривизны ее поверхностей
R1 и R 2 , схематически тонкая линза изображена на рис. 9.3.
F 
Рис. 9.2