Zaochniki_nachertalka / Материалы по Начертательной геометрии / начертательная геометрия лекции / Определение углов

Определение углов

В общем случае угол, составленный пересекающимися или скрещивающимися прямыми общего положения, проецируется на плоскости проекций искаженно.

Однако если стороны угла параллельны плоскости проекций (занимают частное положение прямых уровня), то угол проецируется на эту плоскость в натуральную величину.

Угол между скрещивающимися прямыми измеряется величиной плоского угла, образованного пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.

Угол между скрещивающимися прямыми

Пусть требуется определить величину угла между скрещивающимися прямыми а и b (рис. 1). Для этого через произвольную точку М проводят пересекающиеся прямые сIIа и dIIb. На комплексном чертеже одноименные проекции параллельных прямых соответственно параллельны, т.е. с2IIa2, d2IIb2, с1IIa1, d1IIb1. Затем через прямые с и d проводят горизонталь (или фронталь), после чего треугольник 1М2 переводят в положение плоскости уровня. Все его углы (и в том числе искомый) проецируются на соответствующую плоскость проекций без искажения.

Рисунок 1

Угол между прямой и плоскостью

Угол наклона прямой к плоскости измеряется величиной линейного острого угла, сторонами которого служат прямая и ее проекция на данную плоскость. Однако вместо искомого угла можно найти угол между прямой и перпендикуляром из любой ее точки на плоскость, так как этот угол будет дополнительным до 90° к искомому. Пусть требуется найти угол наклона α

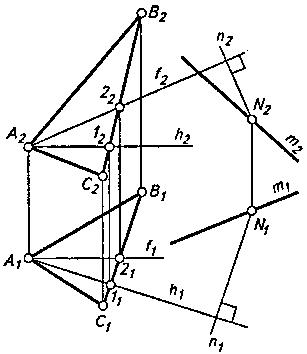
прямой m к плоскости треугольника AВС (рис. 2). Для этого из некоторой точки N прямой m опущен перпендикуляр n к заданной плоскости. Проекции n2 и n1 этого перпендикуляра соответственно перпендикулярны к одноименным проекциям фронтали и горизонтали плоскости треугольника ABC. Угол β между прямыми n и m является дополнительным к искомому углу α, т.е. α = 90°- β.

Рисунок 2

Угол между двумя плоскостями

Двугранный угол (между двумя плоскостями) измеряется линейным острым углом, составленным прямыми пересечения граней с плоскостью, перпендикулярной к ребру двугранного угла, т.е. к линии пересечения двух плоскостей. Линейный угол, служащий мерой двугранного угла, изображается без искажения на плоскости проекций, перпендикулярной его ребру ВС (рис. 3). Однако ребро двугранного угла во многих случаях занимает общее положение относительно плоскостей проекций.

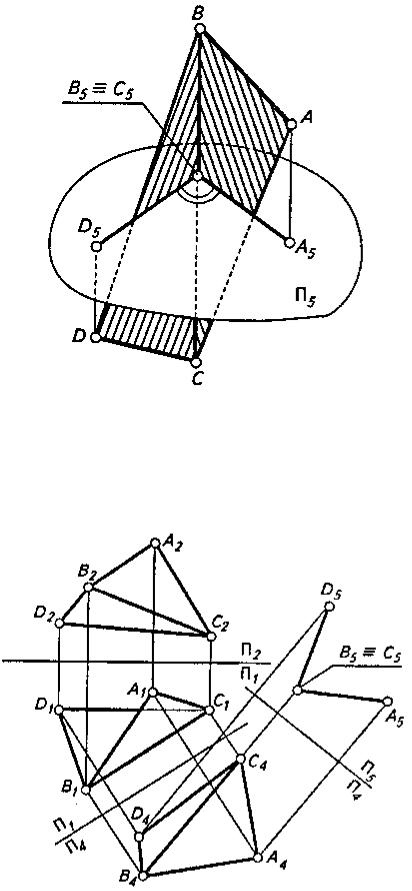
Рисунок 3

В проецирующее положение ребро можно привести последовательным двукратным применением замены плоскостей проекций (рис. 4). При этом в проецирующее положение переходят и грани двугранного угла.

Рисунок 4