Zaochniki_nachertalka / Материалы по Начертательной геометрии / начертательная геометрия лекции / Плоскости, касательные к поверхности

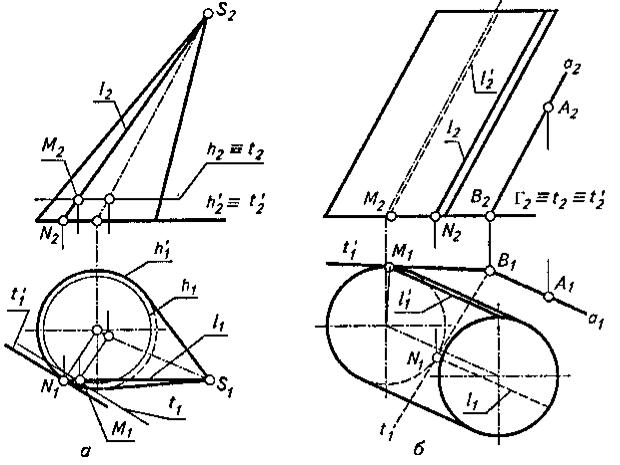
Плоскости, касательные к поверхности

Касательная плоскость - это геометрическое место всех касательных, проведенных к данной кривой поверхности, проходящих через одну ее точку.

Очевидно, что для построения плоскости, касательной к поверхности в какойлибо ее точке, достаточно через эту точку провести на поверхности только две кривые линии и построить к ним касательные прямые в данной точке. Эта пара касательных и определит искомую касательную плоскость.

В зависимости от вида поверхности касательная плоскость может иметь с ней только одну общую точку, например, в случае сферы, или бесконечное их количество, составляющее прямую или кривую линии, например в случае конической поверхности.

Построим плоскость, касательную к поверхности конуса в точке М (рис. 1, а).

Рисунок 1

С этой целью через точку М проведем образующую l (l1, l2). Она является одной из прямых, определяющих касательную плоскость. Второй прямой будет прямая t, касательная к окружности h в ее точке М, проведенная на горизонтальной проекции конуса. Нетрудно видеть, что касательная t параллельна касательной

t’ проведенной в точке N к окружности h’ основания конуса, поэтому окружность h можно не строить.

Проведем через точку А плоскость Θ, касательную к цилиндрической поверхности (рис. 1, б).

Так как касательная плоскость должна содержать в себе образующую цилиндра, то проведем через точку А параллельно ей прямую a. Если теперь провести через точку В - пересечения прямой а с плоскостью Г - прямые t и t’ касательные к окружности основания цилиндрической поверхности, то прямая а и эти касательные определят две искомые касательные плоскости Θ и Θ'. Эти плоскости касаются поверхности цилиндра по ее образующим l и l’.