Zaochniki_nachertalka / Материалы по Начертательной геометрии / начертательная геометрия лекции / Взаимное пересечение поверхностей. Основные понятия

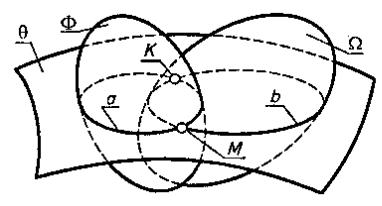
Взаимное пересечение поверхностей. Основные понятия

Линия пересечения двух поверхностей в общем виде представляет собой пространственную кривую, которая может распадаться на несколько частей.

Надо иметь в виду, что проекции линий пересечения всегда располагаются в пределах площади наложения одноименных проекций пересекающихся поверхностей.

При пересечении гранных поверхностей в общем случае получается пространственная ломаная линия.

Обычно линию пересечения двух поверхностей строят по отдельным точкам. При этом требуется выполнить условие инцидентности (взаимопринадлежности) точек и поверхностей. Для чего необходимо и достаточно, чтобы эти точки принадлежали линиям, находящимся в заданных поверхностях и пересекающимся между собой. Точки пересечения таких линий будут общими для заданных поверхностей, т.е. точками их пересечения.

Такие линии получаются при пересечении заданных поверхностей вспомогательными поверхностями или плоскостями-посредниками.

Рисунок 1

В результате можно сформулировать следующий алгоритм построения линии пересечения двух поверхностей;

заданные поверхности, например Ф и Ω (рис. 1), пересекаются вспомогательной поверхностью Θ;

строят линии пересечения а и b поверхностей Ф и Ω вспомогательной поверхностью Θ;

точки пересечения К и М линии а с линией b принадлежат как Ф, так и Ω

выполняют указанные операции необходимое число раз;

соединяя определенным образом полученные точки между собой, строят линии пересечения поверхностей Ф и Ω.

Следует выбирать поверхности-посредники так, чтобы они давали графически простые линии пересечения с заданными поверхностями (например, прямые или окружности).

При составлении в алгоритм не вкладывали никаких конкретных понятий о виде, расположении и способе задания поверхностей Ф и Ω, поэтому приведенный алгоритм является обобщенным, пригодным для решения задач по определению линии пересечения любых поверхностей.

В качестве вспомогательных поверхностей при определении линии пересечения обычно используют плоскости или сферы.