
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
ИНСТИТУТ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ И
ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
КАФЕДРА ИНФОРМАЦИОННЫХ СИСТЕМ
СЕМЕСТРОВАЯ РАБОТА №1 ПО ЧИСЛЕННЫМ МЕТОДАМ
ТАБУЛИРОВАНИЕ ТРАНСЦЕНДЕНТНЫХ ФУНКЦИЙ
ВАРИАНТ 16
Работу выполнил
студент 3 курса группы 09-315
Халиков Р.Р.
Проверила
доцент Глазырина Л.Л.
Казань - 2015
Оглавление
Постановка задачи. 3
Вывод. 9
Листинг программы: 10
12
Список используемой литературы 12
Постановка задачи.
Одна из специальных функций математической физики – интегральный синус, определяется следующим образом:
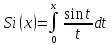 .
.
Цель задания – изучить и сравнить различные способы приближенного вычисления этой функции.
Для этого:
1) Протабулировать Si(x) на отрезке [a,b] с шагом h с точностью ɛ, основываясь на ряде Тейлора, предварительно вычислив его:
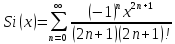 , где
a=0,b=4,h=0.4,
ɛ=10-6 , и получить, таким образом,
таблицу:
, где
a=0,b=4,h=0.4,
ɛ=10-6 , и получить, таким образом,
таблицу:
|
x0 |
x0 |
… |
x0 |
|
f0 |
f0 |
… |
f0 |
 ,
,
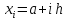 , i=0,…,n.
, i=0,…,n.
2) По
полученной таблице значений построить
интерполяционный полином Лагранжа,
приближающий Si(x):
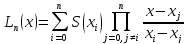 .
.
Затем вычислить погрешность интерполирования
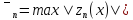 ,
где zn(x)
– погрешность.
,
где zn(x)
– погрешность.
3) Проделать описанные выше действия, взяв в качестве узлов интерполяции равномерно распределенные узлы {xi}, i =0,n и корни полинома Чебышева, вычисляемые по формуле:
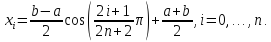
Решение задачи
Для вычисления интерполяционного полинома Лагранжа необходимо построить табличную функцию:
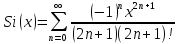 , где
a=0, b=4, h=0.4, ɛ=10-6
.
, где
a=0, b=4, h=0.4, ɛ=10-6
.
Чтобы
избежать переполнения в переменных при
вычислении факториала, избавимся от
него, представив an
в виде произведения an-1
на некое
qn
такое, что:
 .
.
Находим
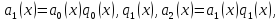 и
так далее, пока:
и
так далее, пока:
 .
.
В
нашем случае:
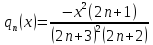 .
.
Таблица и график сумм (равнораспределенные узлы):
|
Xi |
S(Xi) |
|
0 |
0 |
|
0.4 |
|
|
0.8 |
0.772096 |
|
1.2 |
1.108047 |
|
1.6 |
1.389181 |
|
2 |
1.605413 |
|
2.4 |
1.752486 |
|
2.8 |
1.832097 |
|
3.2 |
1.851401 |
|
3.6 |
1.821948 |
|
4 |
1.758203 |
Посчитав интерполяционный полином Лагранжа по формуле:
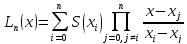 ,
,
получим общую таблицу:
|
xi |
S(xi) |
Ln(xi) |
S(xi)-Ln(xi) |
|
0 |
0 |
0 |
0 |
|
0.4 |
0.396462 |
0.395663 |
0.000798 |
|
0.8 |
0.772096 |
0.772096 |
0 |
|
1.2 |
1.108047 |
1.108316 |
0.000269 |
|
1.6 |
1.389181 |
1.389181 |
0 |
|
2 |
1.605413 |
1.605223 |
0.00019 |
|
2.4 |
1.752486 |
1.752486 |
0 |
|
2.8 |
1.832097 |
1.832355 |
0.000259 |
|
3.2 |
1.851401 |
1.851401 |
0 |
|
3.6 |
1.821948 |
1.821205 |
0.000742 |
|
4 |
1.758203 |
1.758203 |
0 |
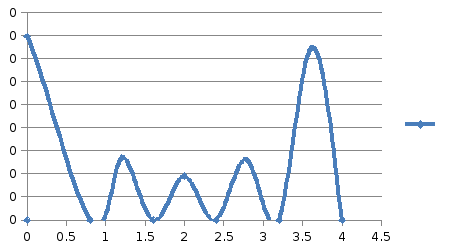 Таблица
и график погрешностей (равнораспределенные
узлы):
Таблица
и график погрешностей (равнораспределенные
узлы):
|
0 |
0 |
|
0.4 |
0.000798 |
|
0.8 |
0 |
|
1.2 |
0.000269 |
|
1.6 |
0 |
|
2 |
0.00019 |
|
2.4 |
0 |
|
2.8 |
0.000259 |
|
3.2 |
0 |
|
3.6 |
0.000742 |
|
4 |
0 |
Максимальная погрешность для n=5 составила 0.000798.
Вычисляем максимальную погрешность
для n<35 по формуле:
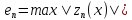 .
.
Получим зависимость:
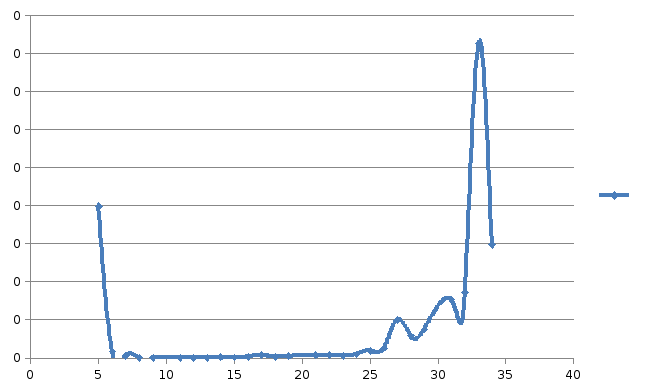
Отсюда мы можем заметить, что с увеличением n погрешность постепенно уменьшается, затем резко возрастает.
Эффект неустойчивости возникает при n=33, максимальная погрешность в этом случае составила 0.0016526.
2 часть задания.
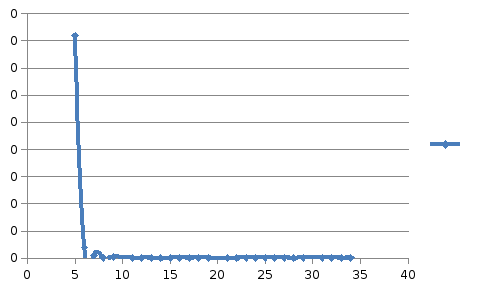
Далее построим интерполяционный полином Лагранжа, взяв в качестве узлов корни полинома Чебышева, вычисляемые по следующей формуле:
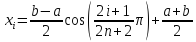 , i=0, …, n, где
n=5.
, i=0, …, n, где
n=5.
Таблица значений функций, значений интерполяционных полиномов Лагранжа и погрешностей (для чебышевских узлов):
|
x_ch |
S_ch |
Ln(x_ch) |
S_ch-L_ch |
|
0 |
0 |
0.000405 |
0.000405 |
|
0.4 |
0.396462 |
0.396154 |
0.000308 |
|
0.8 |
0.772096 |
0.772407 |
0.000311 |
|
1.2 |
1.108047 |
1.108371 |
0.000324 |
|
1.6 |
1.389181 |
1.389034 |
0.000147 |
|
2 |
1.605413 |
1.605003 |
0.00041 |
|
2.4 |
1.752486 |
1.752342 |
0.000144 |
|
2.8 |
1.832097 |
1.832409 |
0.000312 |
|
3.2 |
1.851401 |
1.851695 |
0.000294 |
|
3.6 |
1.821948 |
1.821661 |
0.000287 |
|
4 |
1.758203 |
1.758574 |
0.000371 |
График погрешностей (узлы Чебышева):
|
0 |
|
|
0.4 |
0.000308 |
|
0.8 |
0.000311 |
|
1.2 |
0.000324 |
|
1.6 |
0.000147 |
|
2 |
0.00041 |
|
2.4 |
0.000144 |
|
2.8 |
0.000312 |
|
3.2 |
0.000294 |
|
3.6 |
0.000287 |
|
4 |
0.000371 |
По Чебышевским узлам максимальная погрешность при n=5 составила 0.00041 вместо 0.000798 в предыдущем случае, что доказывает, что чебышевские узлы дают меньшую погрешность и, соответственно, более точный результат.
Зависимость максимальной погрешности от n (для чебышевских узлов):
Как мы видим, погрешность значительно ниже, при использовании чебышевских узлов мы получаем наиболее точные результаты.
Вывод.
В ходе исследования было экспериментально доказано, что интерполирование с использованием чебышевских узлов более точно, чем интерполирование с использованием равнораспределенных узлов.
При увеличении числа точек интерполирования,при использовании равнораспределенных узлов наблюдается убывание погрешности, затем при n=33 погрешность резко возрастает. При использовании чебышевских узлов погрешность всегда убывает.

 0.396462
0.396462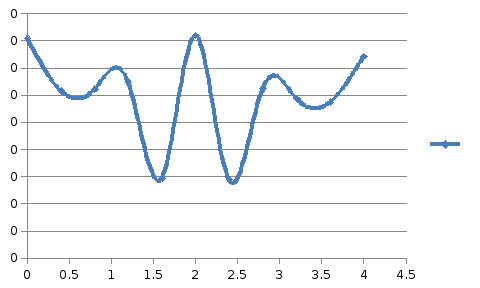 0.000405
0.000405