Решение системы дифференциальных уравнений методом Рунге-Кутты 4-ого порядка точности
.docxФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
ИВМиИТ (ВМК)
КАФЕДРА ИНФОРМАЦИОННЫХ СИСТЕМ
СЕМЕСТРОВАЯ РАБОТА НА ТЕМУ:
«Решение системы дифференциальных уравнений методом Рунге-Кутты 4-ого порядка точности»
Работу выполнил:
студент 3 курса 09-315 группы
Халиков Роман Радиевич.
Работу проверила:
Глазырина Людмила Леонидовна.
“___”_______________ 2016 г.
______________
(подпись)
Казань
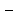 2016
2016
Оглавление
Постановка задачи 3
Решение задачи 3
Вывод 8
Листинг программы 8
Список используемой литературы 9
Постановка задачи
Для решения задачи Коши для системы первого порядка вида
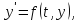
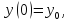
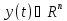 ,
,
использовать метод Рунге-Кутты 4-го порядка точности (правило 3/8):
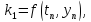
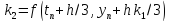 ,
,
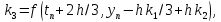
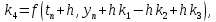
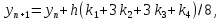
Требуется решить задачу Коши для системы дифференциальных уравнений:
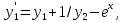
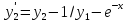
С начальными условиями:
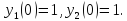
Решаемая система имеет точное решение:
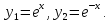
Решение задачи
Рассмотрим задачу Коши для системы дифференциальных уравнений первого порядка вида:
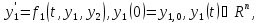
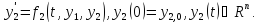
Тогда приближенные значения в последующих точках вычисляются по формулам:
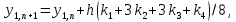
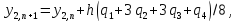
а
коэффициенты
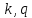 вычисляются последовательно
вычисляются последовательно
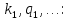
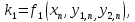
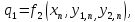
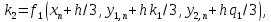
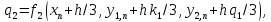
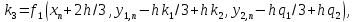
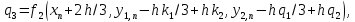
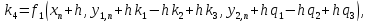
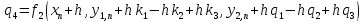 ,
,
где
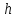 – величина шага на отрезке [0,3].
– величина шага на отрезке [0,3].
При
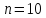 таблица значений функций будет выглядеть
следующим образом:
таблица значений функций будет выглядеть
следующим образом:
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
0,3 |
1,3498588158 |
0,7408182115 |
1,3498588076 |
0,7408182207 |
0,0000000082 |
0,0000000092 |
|
0,6 |
1,8221188312 |
0,5488116186 |
1,8221188004 |
0,5488116361 |
0,0000000308 |
0,0000000175 |
|
0,9 |
2,4596031971 |
0,4065696348 |
2,4596031112 |
0,4065696597 |
0,0000000860 |
0,0000000250 |
|
1,2 |
3,3201171352 |
0,3011941800 |
3,3201169227 |
0,3011942119 |
0,0000002124 |
0,0000000319 |
|
1,5 |
4,4816895611 |
0,2231301216 |
4,4816890703 |
0,2231301601 |
0,0000004908 |
0,0000000385 |
|
1,8 |
6,0496485502 |
0,1652988434 |
6,0496474644 |
0,1652988882 |
0,0000010858 |
0,0000000448 |
|
2,1 |
8,1661722436 |
0,1224563774 |
8,1661699126 |
0,1224564283 |
0,0000023310 |
0,0000000509 |
|
2,4 |
11,0231812753 |
0,0907178965 |
11,0231763806 |
0,0907179533 |
0,0001448946 |
0,0000000568 |
|
2,7 |
14,8797418293 |
0,0672054502 |
14,8797317249 |
0,0672055127 |
0,0006101045 |
0,0000000626 |
|
3 |
20,0855575042 |
0,0497870001 |
20,0855369232 |
0,0497870684 |
0,0007608579 |
0,0000000682 |
Максимальная
погрешность при
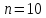 :
:
|
|
|
|
0,0007608579 |
0,0000000682 |
Таблица
зависимости максимальной погрешности
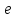 от числа разбиений
от числа разбиений
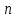 :
:
|
|
|
|
|
|
|
10 |
0,0007608579 |
0,0009334611 |
0,0121737260 |
0,0149353782 |
|
20 |
0,0000412108 |
0,0000484790 |
0,0105499600 |
0,0124106145 |
|
30 |
0,0000076144 |
0,0000090325 |
0,0098682956 |
0,0117061279 |
|
40 |
0,0000023194 |
0,0000027966 |
0,0095000802 |
0,0114548284 |
|
50 |
0,0000009270 |
0,0000011236 |
0,0092703876 |
0,0112360164 |
|
60 |
0,0000004412 |
0,0000005336 |
0,0091492516 |
0,0110644258 |
|
70 |
0,0000002358 |
0,0000002863 |
0,0090580630 |
0,0109985685 |
|
80 |
0,0000001371 |
0,0000001668 |
0,0089827542 |
0,0109301518 |
|
90 |
0,0000000850 |
0,0000001035 |
0,0089200491 |
0,0108634575 |
|
100 |
0,0000000555 |
0,0000000676 |
0,0088731574 |
0,0108195179 |
Графики
зависимости максимальной абсолютной
и относительной погрешности
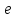 от числа разбиений
от числа разбиений
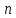 :
:
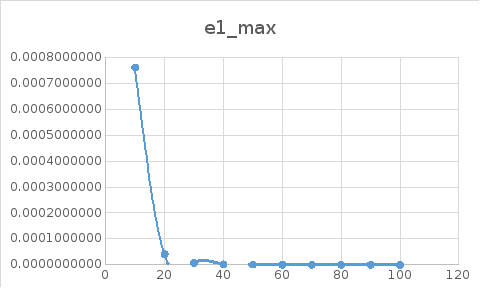
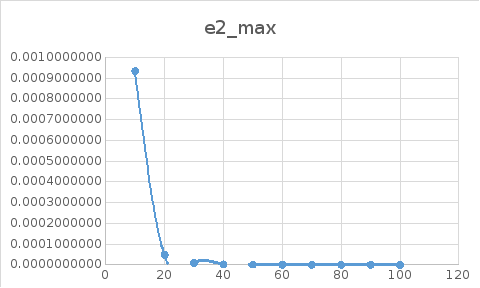
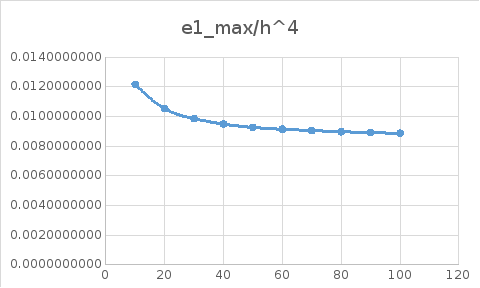
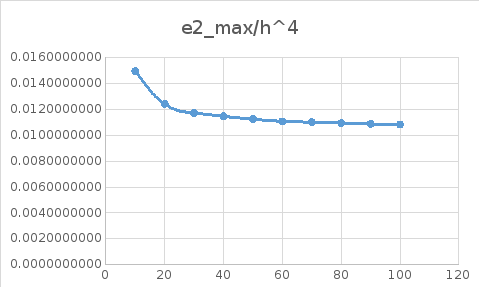
Вывод
Результаты вычислений показали, что с увеличением числа разбиений n максимальная погрешность уменьшается. Результаты показали, что относительные погрешности для каждого решения находятся в интервалах:
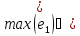 0,0088731574,
0,0121737260),
0,0088731574,
0,0121737260),
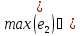 0,0108195179,
0,0149353782).
0,0108195179,
0,0149353782).
Листинг программы
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.IO;
namespace RungeKutta
{
public class RungeKutta
{
public static double max1 = 0;
public static double max2 = 0;
public double t = 0.0;
public double[] Y;
double[] kk, k1, k2, k3, k4;
protected double[] FY;
public RungeKutta(int N)
{
Y = new double[N];
kk = new double[N];
k1 = new double[N];
k2 = new double[N];
k3 = new double[N];
k4 = new double[N];
FY = new double[N];
}
public double[] F(double t, double[] Y)
{
FY[0] = Y[0] + 1.0 / Y[1] - (Math.Pow(Math.E, t));
FY[1] = Y[1] - 1.0 / Y[0] - (Math.Pow(Math.E, -t));
return FY;
}
public void NextStep(double dt)
{
// рассчитать K1
F(t, Y).CopyTo(k1, 0);
//Y==k
for (int i = 0; i < Y.Length; i++)
kk[i] = Y[i] + dt * k1[i] / 3.0; //k2
// рассчитать Y2
F(t + dt / 3.0, kk).CopyTo(k2, 0);
for (int i = 0; i < Y.Length; i++)
kk[i] = Y[i] - dt * k1[i] / 3.0 + dt * k2[i]; //k3
// рассчитать Y3
F(t + 2 * dt / 3.0, kk).CopyTo(k3, 0);
for (int i = 0; i < Y.Length; i++)
kk[i] = Y[i] + dt * k1[i] - dt * k2[i] + dt * k3[i]; //k4
// рассчитать Y4
F(t + dt, kk).CopyTo(k4, 0);
// рассчитать решение на новом шаге
for (int i = 0; i < Y.Length; i++)
Y[i] = Y[i] + dt * (k1[i] + 3 * k2[i] + 3 * k3[i] + k4[i]) / 8.0;//y[n+1]
t = t + dt;
}
static public double[] Solve(double n)
{
double dt = 3.0 / n;
RungeKutta task = new RungeKutta(2);
max1 = 0;
max2 = 0;
task.Y = new[] { 1.0, 1.0 };
//using (StreamWriter sw = new StreamWriter(@"C:\Users\Роман\Desktop\ЧМ-6(debug)("+n+").txt"))
//{
//sw.WriteLine("t \t f1(приблизит.) \t f2(приблизит.) \t f1(точно) \t f2(точно) \t f1(разность) \t f2(разность)");
while (task.t <= 3)
{
if (Math.Abs((task.Y[0]) - func_y1_accurate(task.t)) > max1)
max1 = Math.Abs((task.Y[0]) - func_y1_accurate(task.t));
if (Math.Abs((task.Y[1]) - func_y2_accurate(task.t)) > max2)
max2 = Math.Abs((task.Y[1]) - func_y2_accurate(task.t));
//Запись в файл
// sw.WriteLine("{0:F2}\t {1:F10}\t {2:F10}\t {3:F10}\t {4:F10}\t {5:F10}\t {6:F10}",
// task.t, task.Y[0], task.Y[1], func_y1_accurate(task.t), func_y2_accurate(task.t), Math.Abs(task.Y[0] - func_y1_accurate(task.t)), Math.Abs(task.Y[1] - func_y2_accurate(task.t)));
task.NextStep(dt);
}
//}
return new[] { max1, max2 };
}
static double func_y1_accurate(double x)
{
return Math.Pow(Math.E, x);
}
static double func_y2_accurate(double x)
{
return Math.Pow(Math.E, -x);
}
}
class Program
{
static void Main(string[] args)
{
using (StreamWriter sw = new StreamWriter(@"C:\Users\Роман\Desktop\ЧМ-6(final).txt"))
{
sw.WriteLine("n \t e1_max \t e1_max/h^4 \t e2_max \t e2_max/h^4");
for (int i = 10; i <= 100; i += 10) //n=10...n=100
{
var e_max = RungeKutta.Solve(i);
sw.WriteLine("{0} \t {1:F10} \t {2:F10} \t {3:F8} \t {4:F10}",
i, e_max[0], (double)e_max[0] / Math.Pow(3.0 / i, 4), e_max[1], (double)e_max[1] / Math.Pow(3.0 / i, 4));
}
}
}
}
}
Список используемой литературы
1. Мацокин А. М., Сорокин С. Б. Численные методы: Курс лекций / Новосиб. гос. ун-т. Новосибирск, 2006: Численный анализ. 132 с.
2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы / Издательство «Лаборатория знаний», 7 издание, 2012, 636 с.

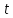
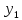 (приблизит.)
(приблизит.)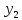 (приблизит.)
(приблизит.)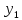 (точно)
(точно)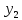 (точно)
(точно)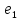
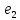
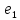
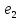
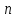
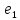 _max
_max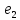 _max
_max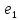 _max/
_max/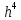
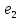 _max/
_max/