всасывающие трубопроводы выполняют по возможности короткими, наибольшего диаметра и с наименьшим числом местных сопротивлений [2, 4, 5, 8].

9.2.3. Изменение пропускной способности трубопроводов в процессе их эксплуатации

При проектировании напорных трубопроводов следует учитывать, что их пропускная способность в период эксплуатации снижается – в некоторых случаях (например, для трубопроводов водоснабжения) до 50% расчетной и даже ниже. Вследствие коррозии и инкрустации (образование отложений в трубах) шероховатость труб увеличивается, что в первом приближении можно оценить по формуле:

– абсолютная шероховатость, мм, через t лет эксплуатации; α – коэффициент, характеризующий быстроту возрастания шероховатости (табл. 9.1), мм/год. Значение коэффициента α зависит от материала труб и свойств жидкости [8].

Таблица 9.1

Значение коэффициента α

9.3.Неустановившееся движение жидкости в трубопроводах

9.3.1.Общие сведения о неустановившемся режиме движения

жидкости в трубопроводах

35

Основным уравнением для неустановившегося движения является уравнение Бернулли, дополненное так называемым инерционным членом. Для элементарной струйки peaльной жидкости уравнение имеет вид:

коэффициенты Кориолиса. Потери напора hw, определяются так же, как при установившемся движении.

Инерционный напор для трубы переменного по длине сечения вычисляется по формуле:

где v=f(l,t), т.е. для того чтобы вычислить интеграл, надо знать закон изменения скорости по длине трубы и по времени.

Для прямолинейной цилиндрической трубы, сечение которой остается постоянным по всей ее длине трубы, сечение которой зависит только от времени. В этом случае частную производную можно заменить на полную:

Примером неустановившегося напорного движения может служить гидравлический удар [8].

9.3.2. Гидравлический удар

36

резервуара. Скорость перемещения этого фронта называется скоростью распространение ударной волны c. Описанный процесс будет продолжаться до тех пор, пока волна не дойдет до резервуара. Этим заканчивается первый этап гидравлического удара, в конце этого этапа вся жидкость в трубе неподвижна, сжата и находится под давлением p+Δp. Некоторый дополнительный объем жидкости из резервуара поступит в трубу.

Второй этап. Начало второго этапа совпадает с окончанием первого. Сжатая жидкость расширяясь, начнет двигаться в сторону резервуара. Сначала придут в движение слои жидкости вблизи резервуара, а затем и более отдаленные, т.е. фронт спада давления n–n начнет повышаться от резервуара к задвижке. К концу фазы вся жидкость в трубе движется со скоростью v в сторону резервуара давление в трубе восстанавливается до первоначального.

Третий этап. Начало третьего этапа характеризуется тем, что жидкость в трубе движется в сторону резервуара со скоростью v. У задвижки возникает слой жидкости, в котором давление на Δр меньше первоначальною. Теперь фронт n-n пониженного давления перемешается в сторону резервуара слева от него давление р, скорость направлена влево, справа жидкость неподвижна, давление в ней на Δρ ниже нормального, Третий этап заканчивается приходом фронта n–n к резервуару.

Четвертый этап. Начало четвертого этапа характеризуется тем, что давление у входа в трубу со стороны резервуара р, а со стороны трубы меньше на Δp, т.е. р–Δp . Такое неуравновешенное состояние приведет к тому, что жидкость из резервуара начнет втекать в трубу со скоростью v и в ней будет повышаться до р.

Фронт первоначального давления n–n теперь перемещается в сторону задвижки. Скорость перемещения слоя равна скорости распространения ударной волны. К концу четвертого этапа скорость во всей трубе равна v, а давление р. Так как задвижка закрыта, то, начиная с конца четвертой этапа, процесс гидравлического удара начнет повторяться. Часть энергии жидкости при гидравлическом ударе переходит в теплоту, поэтому амплитуда колебаний давления с течением времени затухает и процесс приостанавливается [8].

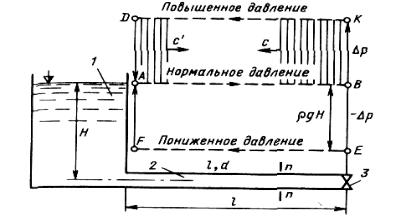
На рис. 9.9 дана диаграмма изменения давления в трубе после быстрого закрытия задвижки без учета потерь энергии. В момент закрытия давление у задвижки 3 подскакивает на Δp по сравнению с обычным, равным ρgH, т.е. давление которое установится во всей горизонтальной трубе после медленного закрытия задвижки. На диаграмме от точки В отложен отрезок Δр вверх от точки А. Это

38

повышение давление затем будет распространяться по трубе от задвижки к резервуару со скоростью с. На этом заканчивается первый этап гидравлическою удара.

Однако у отверстия в резервуаре слева будет действовать давление ρgH, справа ρgH + Δр. Это приведет к тому, что вода из трубы послойно будет втекать в резервуар, а давление уменьшится на Δр, т.е. восстановится до нормы. Иными словами, волна нормального давления (отраженная волна) «побежит» от точки А к точке В со скоростью с', причем с'=с. На этом заканчивается первая фаза гидравлического удара.

На временной диаграмме (рис. 9.9) левый верхний заштрихованный прямоугольник показывает дополнительное давление +Δр и его продолжительность у задвижки, последняя равна времени пробега двойной длины трубы со скоростью распространения ударной волны с.

Затем в начале третьего этапа давление у задвижки падает на – Δр от точки В до точки Е и волна пониженного давления движется по трубе от задвижки к резервуару. На диаграмме – линия EF.

В начале четвертого этапа давление в начале трубы восстанавливается до нормы (отрезок FΆ) и давление ρgH распространяется от резервуара к задвижке (линия АВ).

На временном графике заштрихован прямоугольник с давлением Δр. Продолжительность пребывания пониженного давления у задвижки равна интервалу от 21/с до 41/с. В дальнейшем процесс снова повторяется. Диаграмма давлений на рис. 9.9 описывает своеобразную восьмерку BKDABEFAB [8].

Рассмотрим слой жидкости от задвижки до сечения n-n длиной Δl и площадью поперечного сечения w (рис. 9.9). Остановившаяся масса жидкости (m) в этом объеме потеряла количество движения за время Δt, в течение которого фронт повышенного давления передвинулся от

Импульс силы за тот же промежуток времени равен ΔpwΔt. Справа от сечения n–n давление p + Δp. слева от него – р. Произведение Δρw есть сила, остановившая объем жидкости w Δl за время Δt. Приравняв импульс силы к количеству движения получим:

Откуда:

Δp=ρ Δlv/Δt,

39

где v скорость в трубопроводе до закрытия задвижки и поскольку Δl/Δt – скорость распространения ударной волны c, запишем:

Эта формула была впервые получена Η.Е. Жуковским.

В реальных условиях процесс гидравлического удара протекает несколько иначе, так как при 6ольших давлениях, сопровождающих гидравлический удар, сказывайся как сжимаемость жидкости, так и упругость стенок водовода. Для случая упругих стенок Η.Ε. Жуковским была получена также формула для определения скорости ударной волны [9]:

где r – плотность жидкости; d – внутренний диаметр трубы, d – толщина стенок трубы; Eж – модуль упругости жидкости (кг/м3), Етр – модуль упругости материала стенок трубы.

Если труба абсолютно жесткая Етр®∞, то с0=Ö Eж/r, тогда скорость распространения ударной волны с0 при абсолютно жестких стенках трубопровода равна скорости распространения звука в воде (с0=1425 м/с) и для воды:

Формула справедлива для так называемого прямого удара, т.е. когда время закрытия задвижки меньше фазы удара tз<T (T=2L/c, где L – длина трубопровода от места его перекрытия до сечения в котором давление считается постоянным).

Если tз>T удар называют непрямым, и ударное повышение давления Δp будет меньше определяемого по формуле. При таких условиях повышение давления можно найти по формуле Мишо:

При условии, что tз=T результаты расчетов по этим формулам одинаковы [9].

40