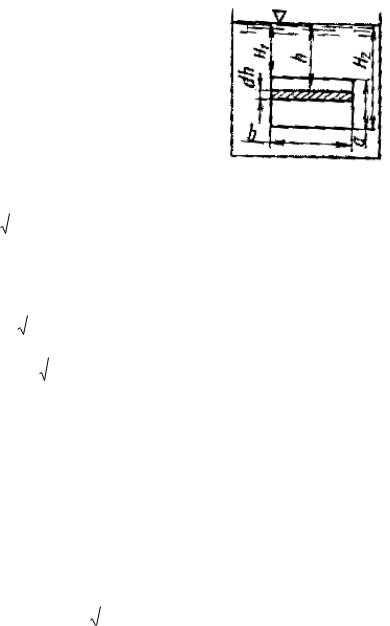
8.2.2. Истечение жидкости через большие отверстия прямоугольной формы
При истечении жидкости через большие отверстия прямоугольной формы (рис. 8.3) скорость движения по его высоте будет различна, поэтому сначала найдем расход, проходящий через малое отверстие высотой dh на глубине h под свободной поверхностью жидкости и шириной b, в котором скорость можно считать одинаковой [8]:
dQ=mbdh |
|
. |
(8.21) |
2gh |
Расход через большое отверстие будет равен:
Рис.8.3. Истечение жидкости через прямоугольные большие отверстия
|
|
|
H2 |
|
|
|
Q = μ b |
2gh |
ò H 1/ 2 dh , |
или |
|||
|
|
|
H1 |
|
|
|
Q=(2/3)mb |
|
|
. |
(8.22) |
||
2g(H2 |
3/2 - H13/2 ) |
|||||
8.2.3. Истечение жидкости через затопленное отверстие
В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении. Для затопленного отверстия формулы для определения скорости и расхода имеют тот же вид, что и для незатопленного отверстия. Разница заключается в том, что под величиной подразумевается в случае затопленного отверстия не глубина погружения, а разность уровней в резервуарах:
Q=mз w |
2g Ho |
, |
(8.23) |
где mз – коэффициент расхода затопленного отверстия, |
|||
определяемый по формуле А.Д. Альштуля: |
|
||
mз=e/mз=e/Ö(2e2m2-e2 n2+x+1 - 2 em) |
(8.24) |
||
где n=w/W отношение площади отверстия к площади сечения потока выше отверстия, m=w/W2 - то же ниже отверстия. Для отверстий малых размеров по сравнению с резервуарами (n® 0, m® 0):
11
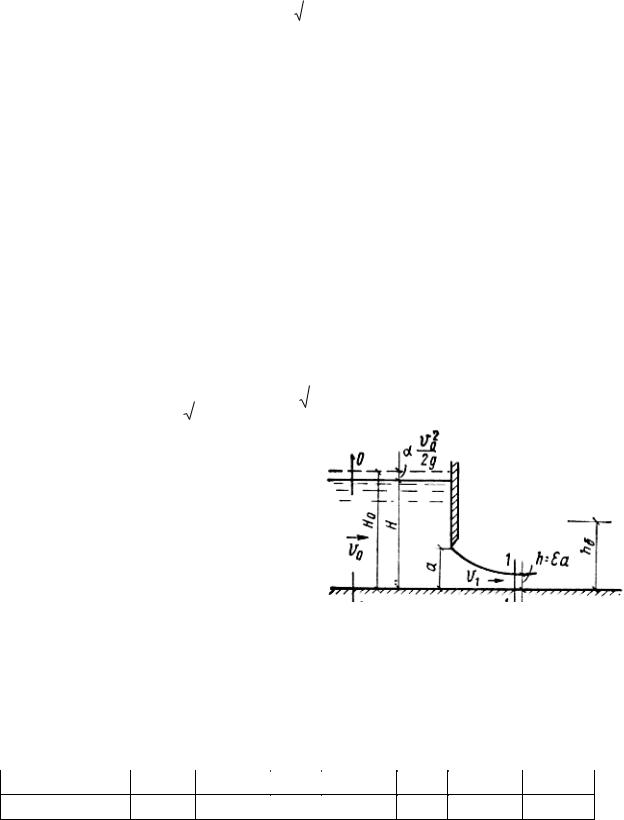
μз=ε/ |
2g Ho |
(8.25) |
т.е. совпадает со значением коэффициента расхода при незатопленном истечении (истечении в атмосферу).
Коэффициент сжатия струи ε и коэффициент сопротивления ξ при истечении при затопленном отверстии практически не отличается от соответствующих коэффициентов при истечении через незатопленное отверстие. Опыт показывает, что коэффициент расхода μ при истечении через затопленное отверстие можно принимать равным коэффициенту μ для незатопленного отверстия [8, 9].
8.2.4. Истечение жидкости из-под затвора
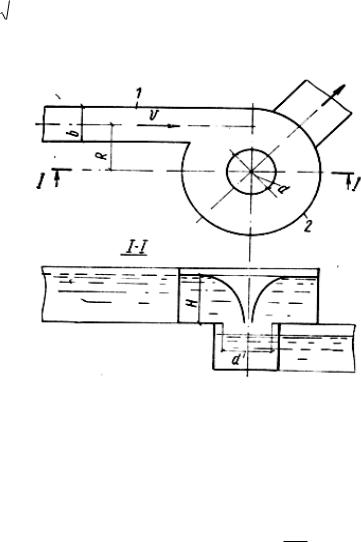
При незатопленном истечении из-под затвора (рис. 8.4) и отсутствии бокового сжатия расход определяют по формуле [8]:
|
|
|
ε |
|
|
|
|
|
|
Q = ϕ |
|
|
|
ba 2gH , |
(8.26) |
||||
|
|
|
|
||||||
|
|
|
|
||||||
1 |
+ ε a / H |
||||||||
|
|
|
|
|
|
||||
где H – глубина воды перед отверстием; а – высота отверстия; b – ширина отверстия; ϕ – поправочный коэффициент, учитывающий влияние потерь напора, значение которого можно принимать по табл. 8.4, в зависимости от числа Фруда.
Значения коэффициента сжатия струи определяются по формуле
εнес=0,57+0,043/(1,1–n),
РисРис. 8..4.8Истеч.4.и еченииние жидкостииз- из-под затвора
под затвора
в которой следует принимать n = a/H.
Таблица 8.1 Поправочный коэффициент учитывающий влияние потерь напора
ϕ |
1,04 |
1,02 |
0,99 |
0,975 |
0,97 |
0,965 |
0,96 |
Fr=v02/2gH |
0,002 |
0,005 |
0,01 |
0,02 |
0,03 |
0,04 |
>0,06 |
8.2.5. Воронкообразование при истечении жидкости |
|
||||||
12
При опорожнении резервуаров через донные отверстия (особенно при малых напорах) над отверстиями могут возникать воронки, создаваемые вращением жидкости вокруг оси, проходящей через центр сливного отверстия. В некоторых случаях воздушная полость (ядро) воронки, пронизывает всю толщу жидкости, проникая в сливное отверстие (так называемая интенсивная воронка); при этом уменьшается рабочая площадь отверстия и снижается его пропускная способность.
Критический напор Нкр, при котором происходит прорыв воздушного ядра воронки в донное отверстие, можно определить по формуле Р. Г. Перельмана:
Нкр/d=0,5(v/ |
|
gd )0,55, |
(8.27) |
|
где d – диаметр отверстия; v0 – средняя скорость истечения в сжатом сечении струи (примерно на 0,5 d ниже плоскости отверстия).
Вихревые |
воронки. |
В |
|
|
|||||
результате |
асимметричного |
|
|
||||||
подвода жидкости к отверстию |
|
|
|||||||
(когда |
|
ось |
подходящего |
к |
|
|
|||
отверстию потока не проходит |
|
|
|||||||
через |
центр |
этого |
отверстия) |
|
|
||||
при |
наличии |
в |
жидкости |
|
|
||||
вихревых |
|
|
|
шпуров |
|
|
|||
преобладающего |
направления |
|
|
||||||
вращения |
(при |
|
обтекании |
|
|
||||
какого-либо препятствия), а |
|
|
|||||||
также |
|
в некоторых |
других |
|
|
||||
случаях |
возникают |
вихревые |
|
|
|||||
воронки. Коэффициент расхода |
|
|
|||||||
донного |
отверстия |
с |
острой |
Рис. 8.4. Донное отверстие с острой кромкой |
|||||
кромкой при наличии вихревой |
Рис.8.5 |
|
|||||||
воронки (рис. 8.5) определяется |
|
|
|||||||
по формуле |
справедливой |
для |
|
|
|||||
μ=0,15…0,60: |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
μ=0,795 – 0,256Е, |
(8.28) |
||
где Е – интенсивность воронкообразования: Е=v(d/R+4R/d) / 
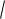gH ,
где R – расстояние в плане от центра отверстия до оси подходящего тока по нормали к последней; v – тангенциальная скорость на радиусе вращения R (значения v и R определяются условиями подхода жидкости
13