откуда, чтобы обеспечить нулевую размерность для двух π- комплексов, приравниваем показатели степени при каждой величине L, Т, М к нулю и получаем системы уравнений:

Решая каждую из двух систем (5.24 и 5.25), находим значения степени для параметров

π1 -комплекса: x=–1, y=2, z=0;

π2 -комплекса: x =−2, y =1, z =0.

Далее определяем структуру комплексов:

π1=gt2/l=g1/v2=1/Fr,

π2=tν/l2=ν/vl=1/Re,

и записываем общий вид критериального уравнения движения вязкой жидкости: f(Fr, Re)=0.

Метод анализа размерностей не всегда позволяет установить искомую зависимость, однако он весьма полезен, когда информации об явлении недостаточно, так как он позволяет провести начальный анализ и рационально организовать экспериментальные исследования [2].

6.РЕЖИМЫ ДВИЖЕНИЯ ЖИДКОСТИ

6.1.Общие сведения

Существует два режима движения жидкости: ламинарный и турбулентный.

Ламинарное движение (от лат. lamina – пластинка), упорядоченное

73

течение жидкости или газа, при котором жидкость (газ) перемещается как бы слоями, параллельными направлению течения. Наблюдаются или у очень вязких жидкостей: нефти, мазута, смазочных масел и в порах грунта при движении подземных вод, или при течениях, происходящих с достаточно малыми скоростями, а также при медленном обтекании жидкостью тел малых размеров. Ламинарное движение имеет место в узких (капиллярных) трубках, в слое смазки в подшипниках, в тонком пограничном слое, который образуется вблизи поверхности тел при обтекании их жидкостью или газом, и др. С увеличением скорости движения жидкости ламинарное движение может в некоторый момент перейти в неупорядоченное турбулентное, при этом резко изменяется сила сопротивления движению.

Турбулентное движение (от лат. turbulentus – бурный, беспорядочный), форма течения жидкости или газа, при которой их элементы совершают неупорядоченные, неустановившиеся движения по сложным траекториям, что приводит к интенсивному перемешиванию между слоями движущихся жидкости или газа. Турбулентный режим движения жидкостей встречается при движении маловязких жидкостей (вода, бензин, спирт) в трубах, каналах, реках. Наиболее детально изучены турбулентные движения в трубах, каналах, пограничных слоях около обтекаемых жидкостью или газом твёрдых тел, а также так называемые свободные турбулентные движения – струи, следы за движущимися относительно жидкости или газа твёрдыми телами и зоны перемешивания между потоками разной скорости, не разделённые какими-либо твёрдыми стенками. Турбулентные движения отличаются от ламинарных как своей сложной внутренней структурой, так и распределением осреднённой скорости по сечению потока и интегральными характеристиками – зависимостью средней по сечению или максимальной скорости, расхода, а также коэффициента сопротивления от числа Re.

Характер режима движения жидкости зависит от соотношения действующих в них сил. Если при движении жидкости преобладают силы вязкости, то режим ламинарный, если преобладают силы инерции, то наблюдается турбулентный режим движения потока. На это обстоятельство указывал в 1880 г. великий русский учёный Д. И. Менделеев и работе «О сопротивлении жидкости и воздухоплавании» которое было полностью изучено в 1883 г. английским физиком Рейнольдсом.

Рейнольдсом были произведены опыты, в которых рассматривался механизм различных видов движения жидкости (рис. 6.1). При разных условиях движения ему удалось установить зависимость между

74

скоростью, геометрическими размерами стенок трубы и вязкостью жидкости. На рисунке показана схема проведения опыта. В напорный бак А подливается вода и устанавливается постоянный напор. В бак вставляется небольшой бачок 6 наполненный красителем (раствор KMn) с плотностью близкой к воде. Из бака отходит труба 1 с постоянным

диаметром d, скорость движения воды по которой регулируется краном 2. Конец трубки 3 заведен в стеклянную трубку 1. Для пополнения сосуда А служив трубка 5 с запорным устройством 6. В напорный бак опускается термометр для определения температуры воды, по которой определяется коэффициент кинематической вязкости.

Производится серия опытов, сопровождаемая визуальными наблюдениями и расчетами.

1-й опыт (рис. 6.1, а): при небольшой скорости струйка красителя

передвигается по трубе.

2-й опыт (рис. 6.1, б): при увеличении скорости струйка имеет волнообразный вид и можно наблюдать эпюру распределения скорости при ламинарном движении с максимальной скоростью в центре.

3-й опыт (рис. 6.1, в): при большой скорости струйка разрушается, вихреобразно распределяется и перемешивается по всему сечению трубы. Жидкость окрашивается и переходит в турбулентный режим движения.

Опыты Рейнольдса показали, что переход от ламинарного типа движения жидкости к турбулентному происходит при

75

определенной критической скорости, значение которой прямо пропорционально кинематической вязкости ν и обратно пропорционально диаметру трубки d:

Чаще всего это выражение записывают через Reкр – безразмерное число Рейнольдса:

Число Рейнольдса при котором ламинарный режим движения жидкости переходит в турбулентный, называют критическим и обозначают Reкp. Опытами установлено, что переход из ламинарного режима в турбулентный происходит при Reкp = 2320. Следовательно, движение в трубах при Re<2320 будет ламинарным, а при Re>2320 – турбулентным.

При безнапорном движении жидкости и для труб некруглого поперечного сечения число Рейнольдса определяют через гидравлический радиус по формуле:

где R=d/4, т.е. критическое число Рейнольдса будет в 4 раза меньше, чем при движении в трубах. Следовательно, при безнапорном движении жидкости при Reкр <580 будет иметь место ламинарный режим, а при Reкр >580 – турбулентный.

Переход ламинарного движения в турбулентное происходит в зоне переходного режима ограниченной двумя значениями скорости – нижней и верхней критическими скоростями течения.

Впористой среде ламинарное движение подчиняется закону Дарси

играница перехода линейной фильтрации к нелинейной определяется также критическим значением числа Рейнольдса, расчетные формулы определения которого имеют более сложный вид, так как учитывают характеристики пористой среды [2].

6.2. Cкорости течения жидкости при ламинарном и турбулентном движении

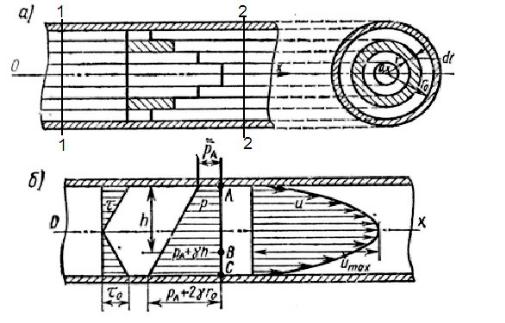
При ламинарном движении жидкости в цилиндрической трубе распределение скоростей по сечению имеет вид параболы и

76

схематически изображается телескопическим (рис. 6.2): у стенок трубы скорости равны нулю, а при удалении плавно возрастают и достигают максимального значения на оси трубы.

Определим закон распределения скоростей в живом сечении потока при ламинарном режиме. Для этого выделим внутри горизонтального трубопровода объем жидкости в виде цилиндра радиусом r (рис. 6.2) и длиной l и составим уравнение равновесия всех действующих сил:

где πr2(P1–P2) – разность сил давления в сечениях 1 и 2; – 2πrlμdu/dr – сила трения на боковой поверхности цилиндра. Знак минус в формуле Ньютона взят потому, что градиент du/dr отрицателен, поскольку с увеличением радиуса скорость убывает.

При равномерном движении жидкости, при котором все живые сечения по длине потока одинаковы как по форме, так и по размерам, и скорости в соответственных точках живых сечений также одинаковы. Таким образом, скорость является функцией исключительно одного радиуса:

C учетом гидравлического уклона I=hw /l =(P1–P2)/γ l получим:

77

Рис. 6.2. Эпюры скорости ламинарном движении жидкости

Расход жидкости через трубу при ламинарном движении численно равен объему параболоида скорости (W=1/2π r02h) и определяется из выражения

отсюда средняя скорость

а соотношение между максимальной и средней скоростью

umax/v=2. (6.12)

Отсюда закон распределения скоростей может быть записан таким образом:

Турбулентный режим движения жидкости характеризуется беспорядочным движением частиц. При этом режиме частицы жидкости движутся по произвольным траекториям и с различной скоростью,

78

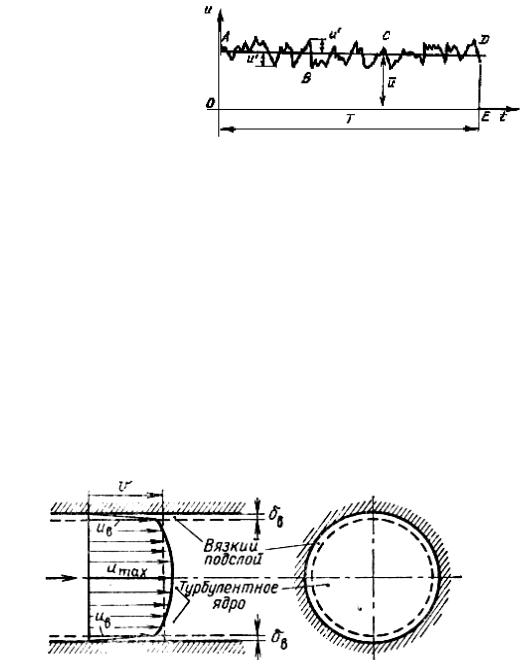
местной скорости (u’) называется пульсацией скорости (рис. 6.3). А среднюю по времени скорость называют осредненной местной скоростью, или осредненной скоростью (u*). Аналитически связь между осредненной скоростью и мгновенной скоростью может быть выражена зависимостью

где T – период наблюдений.

Распределение осредненных скоростей течения в живом сечении трубопровода, полученное на основе опытных данных, может быть представлено схематически (рис. 6.4.).

Рис. 6.4. Распределение осредненных скоростей течения в живом сечении трубопровода

Распределение скоростей течения при турбулентном режиме выглядит иначе, чем при ламинарном режиме и только в пограничном слое (ламинарная пленка переходной слой) скорости течения изменяются так же. В переходной зоне зарождаются вихри, обусловленные увеличением скорости движения и влиянием выступов шероховатости стенок. Возникающие в пограничном слое вихри проникают в центральную часть потока и образуют ядро турбулентного

79