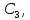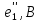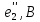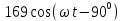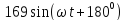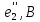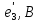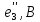вариант 15 (Восстановлен) (2)
.docxЗадача 1.1
Вариант 15
Исходные данные:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
10,5 |
15 |
11 |
7 |
30 |
16,5 |
16,5 |
51 |
30 |
2 |
0 |
Решение
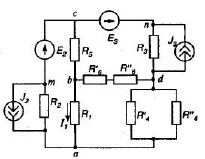
1 Упростить схему, заменив последовательное и параллельное соединенные резисторы четвертой и шестой ветвей эквивалентными:
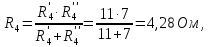
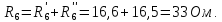
2 Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы.
Составим
уравнения по 1 закону Кирхгофа, число
уравнений
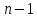 ,
где
,
где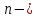 число узлов в схеме,
число узлов в схеме,
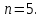

Для
узлов:
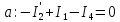
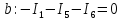
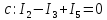
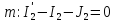
Для
контуров: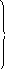
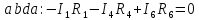
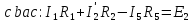

В этих уравнениях все ЭДС и токи, совпадающие с направлением обхода контура, записываются со знаком плюс; ЭДС и токи, направленные навстречу обходу – со знаком минус
3 Определим токи во всех ветвях методом контурных токов.
Выразим
токи ветвей через контурные токи
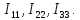
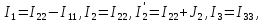
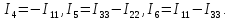
Подставим
данные выражения в систему уравнений,
составленные по 2 закону Кирхгофа. 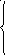
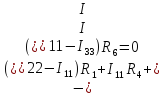
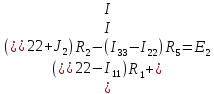


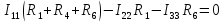
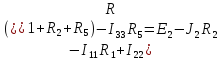
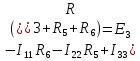
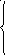
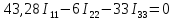
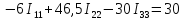
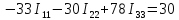
Полученную систему решим по методу Крамера:
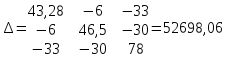
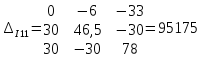
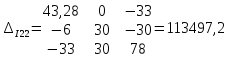
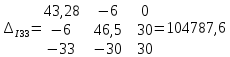
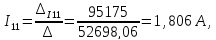


Определим токи в ветвях схемы:
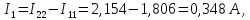
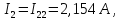

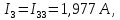
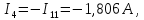
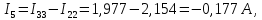
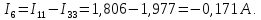
4 Определим токи во всех ветвях методом узловых потенциалов
Преобразуем источник тока в источник ЭДС
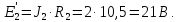

Примем
потенциал
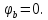
Выразим токи ветвей через потенциалы узлов:


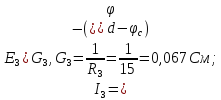
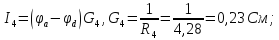
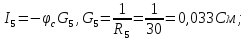
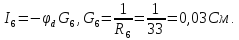
Подставим
данные выражения в уравнения, составленные
по второму закону Кирхгофа.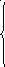
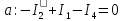

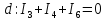

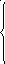
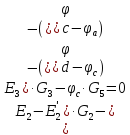
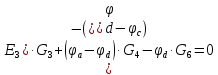
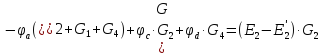
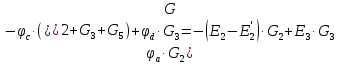
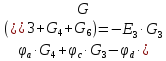
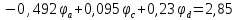
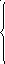
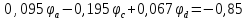
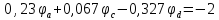
Полученную систему решим по методу Крамера:
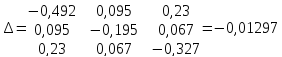
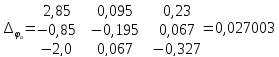
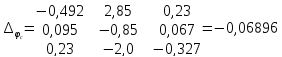
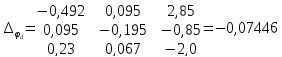
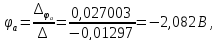
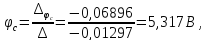

Определим токи в ветвях схемы:
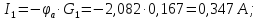
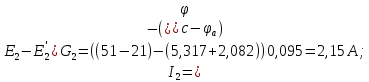
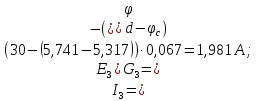
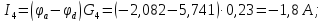
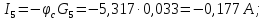
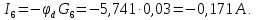
5 Результаты расчета сведем в таблицу
|
Метод расчета |
Токи, А |
|||||
|
I1 |
I2 |
I3 |
I4 |
I5 |
I6 |
|
|
МКТ |
0,348 |
2,154 |
1,977 |
-1,806 |
-0,177 |
-0,171 |
|
МУП |
0,347 |
2,15 |
1,981 |
-1,8 |
-0,177 |
-0,171 |
|
Погрешность % |
0,28 |
0,19 |
0,2 |
0,33 |
0 |
0 |
6 Составим баланс мощности:

Мощность источников энергии:
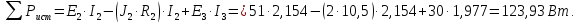
Мощность, приемников, т.е. всех сопротивлений в цепи:
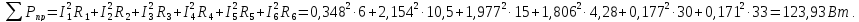
7 Определить ток I1 методом эквивалентного генератора
Разрываем
ветвь с током I1,
на зажимах этой ветви ставим напряжение
 , направление которого совпадает с
направлением тока I1.
, направление которого совпадает с
направлением тока I1.

Определим
напряжение
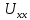 по второму закону Кирхгофа:
по второму закону Кирхгофа:
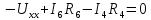
Определим
токи
 методом контурных токов для данной
схемы:
методом контурных токов для данной
схемы:

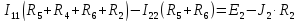
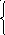




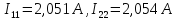
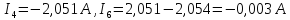
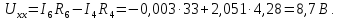
Определим входное сопротивление относительно зажимов выделенной ветви.
Для этого источники ЭДС закорачиваем и один из треугольников сопротивлений преобразуем в эквивалентную звезду:

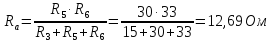
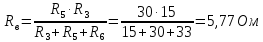
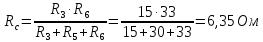


Ток в ветви:
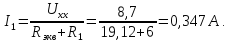
8 Начертим потенциальную диаграмму:

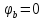

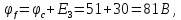
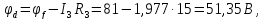
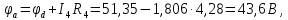

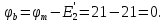
Выберем масштаб mφ = 20 В/см, mR = 4 Ом/см
 Задача
1.2
Задача
1.2
Исходные данные:
|
|
|
|
|
|
|
|
|
|
6,8 |
0,91 |
0,46 |
100 |
3500 |
|
|
|
|
|
|
|
|
0 |
0 |
|
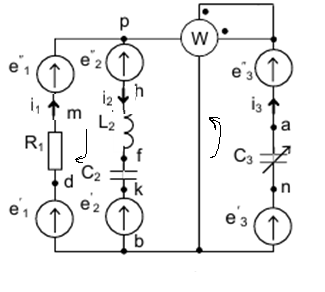
Подготовка исходных данных:
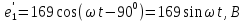
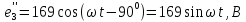
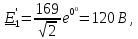
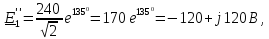
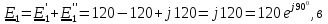
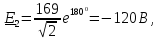

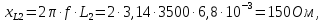
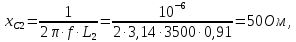

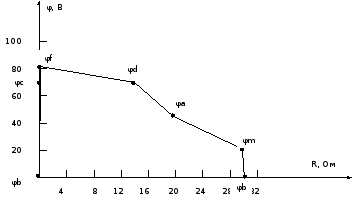
1 На основании законов Кирхгофа составить систему уравнений в двух формах а) дифференциальной; б) символической.
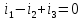
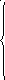
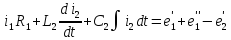
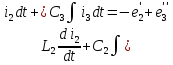
Для составления уравнений в символической форме схему перечертим
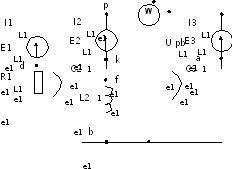
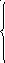
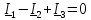
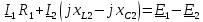

2 Определим комплексы действующих значений токов во всех ветвях МКТ
Выразим токи ветвей через контурные токи:
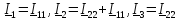
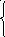
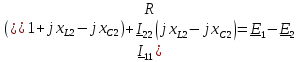
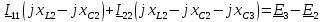
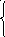
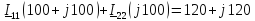
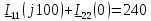
Решим систему методом Крамера:

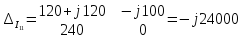

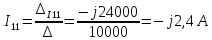
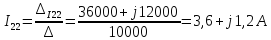
Определим действительные токи в ветвях:

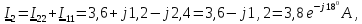

3 Определим показание ваттметра:
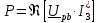
где
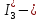 сопряженный ток (изменяется знак перед
мнимой частью)
сопряженный ток (изменяется знак перед
мнимой частью)
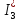 берется
со знаком плюс, так ток входит в зажим
*.
берется
со знаком плюс, так ток входит в зажим
*.
Для
определения
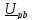 составим уравнение по второму закону
Кирхгофа.
составим уравнение по второму закону
Кирхгофа.
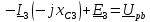

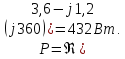
Определим баланс мощности:
- полная мощность источников:
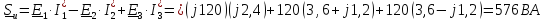
где
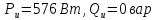
- мощность приемников:
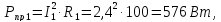

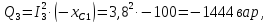

4 Построим топографическую диаграмму, совмещенную с векторной диаграммой токов по внешнему контуру.
Топографическая диаграмма - это диаграмма комплексных потенциалов, причем каждой ее точке соответствует определенная точка в электрической схеме. Потенциал точки а примем равным нулю. Рассчитаем комплексные потенциалы всех точек контура.

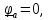
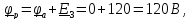
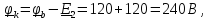


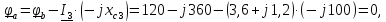

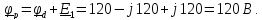
Для построения топографической диаграммы выберем масштаб по току и напряжению, например mI = 1А\см, mU = 50 B\см.

1 Линия bd параллельна с I1, (на активных сопротивлениях угол сдвига фаз между током и напряжением равен нулю).
2 на реактивных элементах угол сдвига фаз между током и напряжением равен 900, поэтому:
линия k f перпендикулярна I2;
линия ba перпендикулярна I3.
5 Построим круговую диаграмму.
Для
построения круговой диаграммы определим
параметры эквивалентного генератора.
Для этого исключим из схемы С3
, а на оставшихся зажимах проставим
напряжение
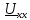 по направлению, совпадающему с током
по направлению, совпадающему с током
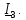 Определим ток
Определим ток
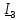 методом эквивалентного генератора.
методом эквивалентного генератора.

В
схеме протекает ток
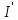 .
Определим ток
.
Определим ток
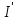 по второму закону Кирхгофа:
по второму закону Кирхгофа:
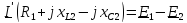
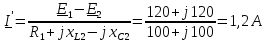
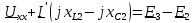
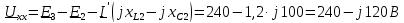
Определим
входное сопротивление схемы
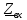 относительно зажимов выделенной ветви
при закороченных источниках ЭДС.
относительно зажимов выделенной ветви
при закороченных источниках ЭДС.

Определим
ток
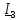 методом эквивалентного генератора:
методом эквивалентного генератора:

Определим ток короткого замыкания:

Определим угол ψ:
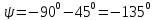
Порядок построения круговой диаграммы
1. Выберем масштаб mI = 1А\см, mZ = 20 B\см.
2.
Отложим на комплексной плоскости вектор
тока
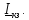
3.
Для нахождения центра окружности строим
два перпендикуляра: первый перпендикуляр
проводим через середину вектора
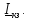 Для построения второго перпендикуляра
вначале строим вспомогательную линию
ab
под углом «+ψ = -1350»
к линии am
и к ней из конца вектора
Для построения второго перпендикуляра
вначале строим вспомогательную линию
ab
под углом «+ψ = -1350»
к линии am
и к ней из конца вектора
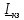 проводим второй перпендикуляр. Точка
О – точка пересечения двух перпендикуляров
является центром окружности.
проводим второй перпендикуляр. Точка
О – точка пересечения двух перпендикуляров
является центром окружности.
4.
По линии cm
откладываем в масштабе модуль
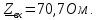 Затем от конца отрезка
Затем от конца отрезка
 под углом «-ψ =1350»
строится линия нагрузки. На линии
нагрузки в масштабе откладывается Zн.
под углом «-ψ =1350»
строится линия нагрузки. На линии
нагрузки в масштабе откладывается Zн.

6 Пользуясь круговой диаграммой, построить график изменения тока в изменяющемся сопротивлении в зависимости от модуля этого сопротивления.

7
Используя данные расчётов, полученных
в пунктах 2-5 записать выражение для
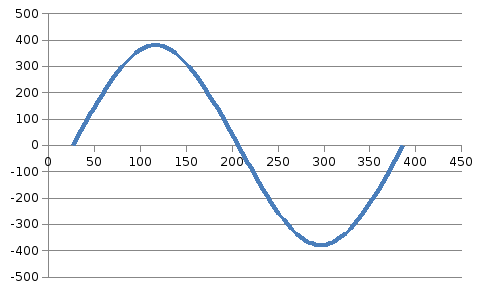
мгновенного напряжения
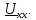
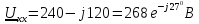

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wt |
|||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
8 Полагая, что между двумя любыми индуктивными катушками, расположенными в различных ветвях заданной схемы, имеется магнитная
связь при взаимной индуктивности, равной М, составить в общем виде
систему уравнений по законам Кирхгофа для расчёта токов во всех ветвях
схемы, записав её в двух формах: а) дифференциальной; б) символической.

а) дифференциальная форма:
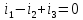
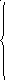
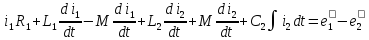
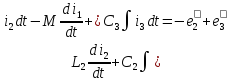
б) символическая форма:
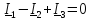

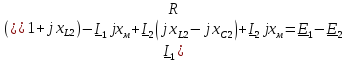


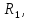
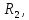

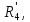
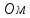
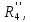
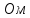


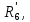
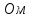
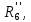
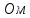

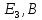

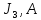
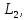
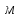 Гн
Гн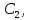
 кФ
кФ