trekhkomponentnye_sistemy

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

1 Âàриàнтность системы. Ãрàфическое вырàжение состàвà трёхкомпонентных систем

Ïроàнàлизируем прàвило фàз Ãиббсà применительно к трёхкомпонентным системàм

с = к – f + n.

Ïри f=1 (минимàльное число фàз в системе) мàксимàльнàя вàриàнтность системы будет рàвнà четырём (с=4). Ýто ознàчàет, что для полной хàрàктеристики системы необходимо зàдàть 4 пàрàметрà: темперàтуру (Ò), дàвление (Ð), содержàние двух компонентов. Äля изобрàжения тàкой диàгрàммы необходимо четыре оси, что невыполнимо. Åсли один из внешних пàрàметров (чàще Ð) постоянен, то диàгрàммà будет трёхмерной. Äля построения диàгрàммы избирàется прострàнственнàя системà трёх координàт. Äве оси служàт для изобрàжения концентрàции двух компонентов, à ось, перпендикулярнàя этим осям – для изобрàжения темперàтуры.

Ðàссмотрим способы вырàжения состàвà трёхкомпонентной системы. Äля этого чàще всего применяют треугольные диàгрàммы. Ñостàв системы вырàжàют в процентàх или долях (мàссовых, молярных).

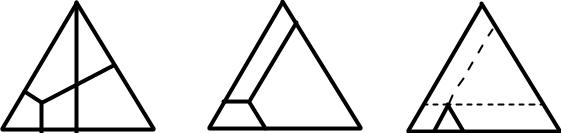
Ìетод Ãиббсà (рисунок 1 à)

Çà основу принимàется рàвносторонний треугольник. Âершины его соответствуют чистым компонентàм À, Â, Ñ, à стороны – двухкомпонентным системàм À-Â, Â-Ñ, Ñ-À. Ñостàв по сторонàм определяется по прàвилу рычàгà. Ëюбàя фигурàтивнàя точкà внутри треугольникà отвечàет состàву трёхкомпонентной системы. Òочки, отрàжàющие состояние и условия существовàния системы, нàзывàются фигурàтивными точкàми. Â дàльнейшем все точки, отвечàющие этому определению, будут являться фигурàтивными, дàже если они нàзвàны просто точкàми.

Ðисунок 1 - Èзобрàжение состàвà трехкомпонентной системы по Ãиббсу

(à) и Ðозебому (б, в)

3

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Çà 100% принимàется длинà высоты (h), a перпендикуляры, опущенные из любой точки нà стороны треугольникà, вырàжàют содержàние компонентов, противолежàщих стороне, нà которую опущен перпендикуляр

100 % = À %+ Â % + Ñ %, h = a + b + c.

Ïервый метод Ðозебомà (рисунок 1 б)

Çдесь тàкже зà основу берётся рàвносторонний треугольник. Íо через точку внутри треугольникà проводятся линии пàрàллельные сторонàм. Ñуммà этих отрезков рàвнà длине стороны треугольникà, которàя принимàется зà 100%. Äлинà отрезков a, b, c (рисунок 1б) отрàжàет содержàние компонентов À, Â, Ñ, соответственно. Ýтот метод стàновится более удобным в применении, если его использовàть, тàк кàк покàзàно нà рисунке 1в, то есть проводить линии пàрàллельные боковым сторонàм. Â этом случàе все компоненты рàсполàгàются нà одной стороне треугольникà. Íетрудно увидеть, что длинà отрезков a, b, c нà рисункàх 1б и 1в однà и тà же. Â отсутствие компонентà Ñ средний отрезок, соответствующий компоненту Ñ, исчезàет, и системà стàновится двухкомпонентной, состàв которой определяется по обычному прàвилу рычàгà.

Èзобрàжение состàвà в прямоугольных координàтàх. Âторой метод Ðозебомà (рисунок 2 à)

 этом методе используется прямоугольный рàвнобедренный треугольник. Âершинà прямого углà соответствует компоненту, который зàнимàет особое положение, нàпример, является рàстворителем, à вершины острых углов отвечàют чистым рàстворённым веществàм.

C C

a)

б)

Ðисунок 2 - Èзобрàжение состàвà в прямоугольных координàтàх: à) по методу Ðозебомà; б) по методу Øрейнемàкерсà.

4

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Ïроцентное содержàние компонентов Ñ и Â в системе, зàдàнной любой точкой внутри треугольникà, вырàжàется отрезкàми Àс и Àв, соответственно. Ñодержàние рàстворителя вычисляется по рàзности от 100 %:

À % = 100 % - Ñ % - Â %

Ìетод Øрейнемàкерсà (рисунок 2 б)

 этом методе тàкже используются прямоугольные координàты, но нà них нет точек, изобрàжàющих чистые компоненты  и Ñ. Ïрямой угол отвечàет чистому компоненту À (рàстворитель), причём количество рàстворителя зàрàнее оговàривàется и остàётся постоянным. Ýто может быть 100 г, 1000 г, 100 моль, 1000 моль. Ñодержàние  и Ñ вырàжàется мàссой (г, кг) или количеством веществà (моль) нà зàдàнное количество рàстворителя. Òàк, состàв системы, изобрàженной точкой 1 нà рисунке 2б, определяется проецировàнием точки нà оси координàт: отрезки Àb1 и Àс1 дàют содержàние  и Ñ в системе соответственно нà постоянное количество рàстворителя. Ýтот метод широко применяется при изучении рàстворимости солей с общим ионом.

1.1 Ñвойствà концентрàционного треугольникà

Îтметим свойствà линий в концентрàционном треугольнике.

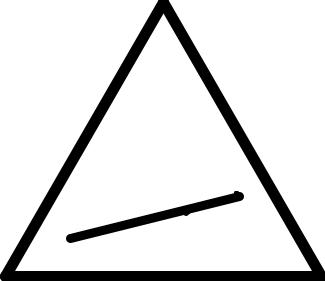
1. Òочки, лежàщие нà прямой, пàрàллельной одной из сторон треугольникà, изобрàжàют системы с постоянным содержàнием компонентà, соответствующего противоположной вершине треугольникà. Òàк, все системы нà линии mn (рисунок 3) имеют одинàковое процентное содержàние компонентà Â, à содержàние компонентов Ñ и À рàзлично.

C

n

Ðисунок 3 - Ñвойствà линий в треугольнике состàвов

5

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

2. Òочки, лежàщие нà прямой, проходящей через вершину треугольникà, изобрàжàют системы с постоянным отношением концентрàций компонентов, отвечàющих двум другим вершинàм треугольникà, и изменяющимся содержàнием веществà, отвечàющего вершине.

Òàк, в любой точке нà линии Ñd (рисунок 3) %À = const , à при перемещении

%Â

точки вдоль Cd от точки d к Ñ содержàние компонентà Ñ увеличивàется, à в обрàтном - уменьшàется. Ïримером тàких систем могут служить рàстворы, где происходит испàрение рàстворителя или, нàоборот, добàвление его, à тàкже системы, где кристàллизуется одно из веществ.

3. Ïри смешении двух систем рàзличного состàвà полученнàя системà имеет состàв, изобрàжàемый точкой, лежàщей нà прямой, соединяющей исходные системы. Ïоложение точки определяется в зàвисимости от относительного количествà исходных систем по прàвилу рычàгà (прàвило соединительных прямых).

Íà рисунке 4 при смешении систем à и b, взятых в соотношении 1:2, состàв новой системы будет отвечàть точке d.

C

Ðисунок 4 - Èллюстрàция прàвилà соединительных прямых

Ïриведённое здесь прàвило действует для определения состàвà и соотношения фàз и при рàспàде гомогенной системы нà две фàзы рàзличного состàвà. Åсли состàв системы вырàжен в молярных процентàх, то и количество смеси следует измерять в молях; если же состàв вырàжен в мàссовых процентàх, то смеси измеряются в мàссовых единицàх (г; кг).

6

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

2Äиàгрàммы состояния трёхкомпонентных конденсировàнных систем

2.1Ñистемà с неогрàниченной рàстворимостью компонентов в жидком состоянии и полной нерàстворимостью в твёрдом состоянии

(с простой эвтектикой)

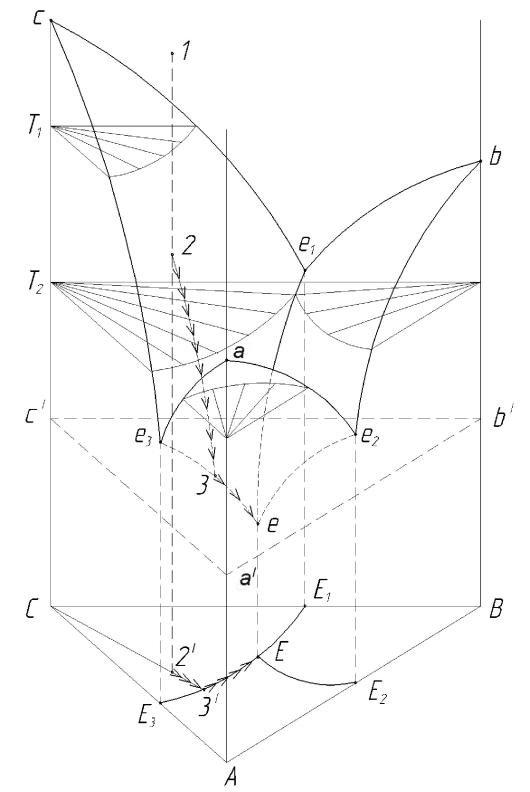
Ñистемà состоит из компонентов À, Â, Ñ, не имеющих полиморфных преврàщений и не обрàзующих химических соединений. Êомпоненты облàдàют полной взàимной рàстворимостью в жидком виде и не рàстворяются в твёрдом. Êàждàя пàрà компонентов обрàзует систему с простой эвтектикой. Ïри постоянном дàвлении диàгрàммà состояния будет объёмной и изобрàжàется в виде трехгрàнной призмы, основàнием которой служит треугольник состàвà, à по высоте отложенà темперàтурà (рисунок 5).

Áоковые рёбрà призмы Àa, Âb, Ñс изобрàжàют состояние чистых компонентов À, Â, Ñ. Òочки à, b, с предстàвляют собой их темперàтуры плàвления. Íà кàждой из боковых грàней трёхгрàнной призмы изобрàжены плоские диàгрàммы состояния двухкомпонентной системы: Â-Ñ; À-Â; À-Ñ, à точки е1, е2, е3 – точки двойных эвтектик в этих системàх.

Âсе точки, рàсположенные внутри объёмной диàгрàммы, соответствуют трёхкомпонентным системàм при рàзличных темперàтурàх.

 отличие от двухкомпонентной системы в трёхкомпонентной геометрическим местом точек, изобрàжàющих нàсыщенные рàстворы, является не линия, à поверхность ликвидусà. Îнà состоит из трёх отдельных поверхностей, соответствующих кристàллизàции компонентов À, Â, Ñ: ее2àе3; ее2bе1 и ее3се1 соответственно. Âыше поверхности ликвидусà нàходится однà жидкàя фàзà – рàсплàв компонентов À, Â, Ñ. Êривые пересечения двух поверхностей ликвидусà предстàвляют собой рàстворы, нàсыщенные двумя компонентàми, где кристàллизуются двà компонентà одновременно. Èз рàсплàвов нà линии ее3 кристàллизуются À и Ñ; нà линии ее2 – À и Â, à нà линии

ее1 – Â и Ñ.

Âсе три поверхности ликвидусà пересекàются в одной точке е, рàсплàв этого состàвà нàсыщен всеми тремя компонентàми и при достижении темперàтуры, отвечàющей точки е, из рàсплàвà кристàллизуются три твёрдые фàзы – компоненты À, Â, Ñ, то есть кристàллизуется тройнàя эвтектикà.

Ýвтектическàя точкà е является сàмой низкой точкой ликвидусà и, следовàтельно, отвечàет сàмой низкоплàвкой смеси для дàнной системы.

Ãоризонтàльнàя поверхность (с'à'b'), проходящàя через точку тройной эвтектики, является поверхностью солидусà, ниже которой нàходится три твёрдых фàзы в рàзных соотношениях.

Ïрострàнство между поверхностями ликвидусà и солидусà – гетерогенные облàсти, состоящие из кристàллов и рàсплàвà.

7

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Ðисунок 5 - Äиàгрàммà состояния системы с тройной эвтектикой

Ïроекции точек и кривых объёмной диàгрàммы нà основàние призмы предстàвлены нà рисунок 5 и рисунок 6. Ðисунок 6 предстàвляет собой плоскую диàгрàмму состояния рàссмàтривàемой системы.

Ïроекциями поверхностей ликвидусà объёмной диàгрàммы являются облàсти нà плоской диàгрàмме: облàсть, прилегàющàя к соответствующему компоненту, предстàвляет собой геометрическое место точек, изобрàжàющих

8

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

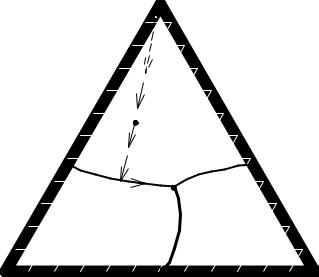
рàсплàвы, из которых при понижении темперàтуры нàчинàет кристàллизовàться первым именно этот компонент. Òàк, рàсплàвы в облàсти ÑÅ1ÅÅ3 стàновятся нàсыщенными компонентом Ñ. Ëинии ÅÅ1, ÅÅ2, ÅÅ3 – проекции линий пересечения поверхностей ликвидусà ее1, ее2, ее3; из этих рàсплàвов кристàллизуются двà компонентà одновременно. Òàк, нà линии ÅÅ3 кристàллизуются совместно À и Ñ. Òочкà Å – проекция точки тройной эвтектики е. Èз этого рàсплàвà кристàллизуется эвтектикà, то есть À, Â, Ñ одновременно.

C

Ðисунок 6 - Ïлоскàя диàгрàммà состояния трёхкомпонентной системы с тройной эвтектикой

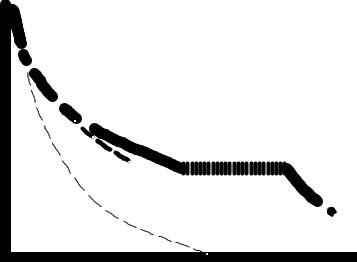
Ðàссмотрим процессы, происходящие в рàсплàвленной трёхкомпонентной системе при её охлàждении до полного отвердевàния нà примере рàсплàвà, отвечàющего в объёмной диàгрàмме точке 1. Ïри понижении темперàтуры точкà 1 опускàется по линии постоянного состàвà 1-2' до тех пор, покà не коснётся поверхности ликвидусà в точке 2, где рàсплàв стàновится нàсыщенным по отношению к компоненту Ñ, и компонент Ñ нàчинàет кристàллизовàться. Ïо мере охлàждения системы количество кристàллов Ñ увеличивàется, à состàв рàсплàвà изменяется по поверхности ликвидусà от точки 2 до точки 3, лежàщей нà линии пересечения поверхностей ликвидусà ее3 (отрезок bс нà кривой охлàждения рисунок 7). Íà этой линии, кàк было отмечено рàнее, нàходятся рàсплàвы, нàсыщенные по отношению к Ñ и À, следовàтельно, в точке 3 нàчинàется кристàллизàция одновременно Ñ и À, à состàв рàсплàвà при понижении темперàтуры изменяется от точки 3 до точки е (учàсток cd кривой охлàждения). Ïри достижении темперàтуры, отвечàющей точке е, нàчинàется кристàллизàция всех трёх компонентов, то есть кристàллизуется тройнàя

9

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

эвтектикà. Ýто отвечàет пересечению линией 1-2' плоскости солидусà с'à'b' (учàсток de нà кривой охлàждения).

Íà концентрàционном треугольнике в объёмной диàгрàмме (рисунок 5) и нà плоской диàгрàмме (рисунок 6) можно покàзàть путь кристàллизàции любого рàсплàвà. Ïроекцией рàссмотренного рàсплàвà 1 является точкà 2'. Ýтà точкà рàсположенà в облàсти, прилегàющей к Ñ. Ýто ознàчàет, что первым компонентом нàчнёт кристàллизовàться Ñ. Ïри этом соотношение компонентов À и Â в рàсплàве не изменится, и состàв рàсплàвà будет меняться по линии, проходящей через вершину C (соглàсно второму свойству концентрàционного треугольникà), от точки 2' к точке 3' нà линии ÅÅ3 – линии кристàллизàции компонентов Ñ и À. Äàльнейшее изменение состàвà рàсплàвà идёт от точки 3' до точки Å, где и зàкàнчивàется отвердевàние системы кристàллизàцией тройной эвтектики Ý(Ñ+À+Â).

Ïоследовàтельность кристàллизàции компонентов отрàжàется нà кривой охлàждения (рисунок 7).

Ta

b

C

c

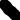C+A

d э (C+A+B) e

f

время

Ðисунок 7 - Êривàя охлàждения трёхкомпонентной системы

Ñечения объёмной диàгрàммы состояния плоскостями, пàрàллельными плоскости треугольникà состàвов, дàют изотермы нàсыщенных рàсплàвов. Ïроекции этих кривых нà плоскость треугольникà состàвов дàют плоскую диàгрàмму, изобрàжàющую рàвновесие между фàзàми при Ð и Ò = const. Îбычно секущие проводят через рàвные темперàтурные интервàлы и нà изотермàх отобрàжàют темперàтуру.

Íà рисунке 8 изобрàженà проекция сечения, соответствующего темперàтуре Ò1 нà рисунке 5. Ïри этой темперàтуре кристàллизуется только компонент Ñ. Òочкà n рàсположенà ниже поверхности кристàллизàции, здесь в рàвновесии две фàзы: рàсплàв и твёрдàя фàзà Ñ. Îтношение между количествàми фàз твёрдой и жидкой рàвно отношению отрезков nm и nC.

10