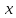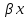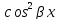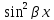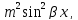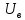вариант 14 ДЛ

Вариант 15

Исходные данные:

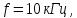
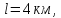
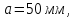
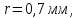
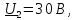
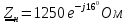
Решение

1 Определим первичные параметры линии:

- сопротивление проводов двухпроводной линии с медным проводом на постоянном токе:

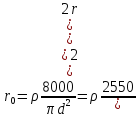
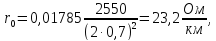
- поправочный коэффициент 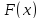, учитывающий увеличение активного сопротивления за счет поверхностного эффекта:

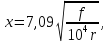
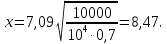
Используя таблицу 2, определяем 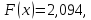тогда

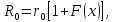
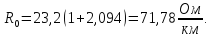
Индуктивность двухпроводной линии:

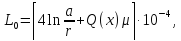
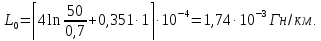
Емкость двухпроводной линии на единицу длины:

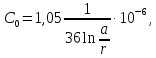
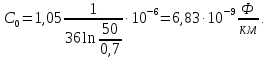
Проводимость единицы длины:

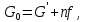
где 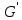- проводимость изоляции на постоянном токе, равная 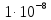См/км

при сухой погоде;

n – коэффициент диэлектрических потерь, равный 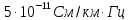при сухой погоде.

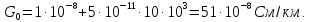
2. Рассчитаем напряжение 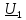и ток 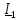в начале линии, активную Р и полную S мощности в начале и в конце линии, а также КПД линии.

Напряжение и ток находятся по уравнениям длинной линии в гиперболических функциях.

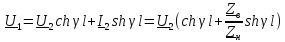
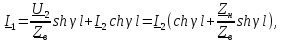
где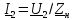

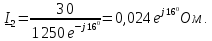
Вычислим волновое сопротивление 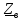и постоянную распространения 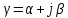, для чего определим погонные реактивные сопротивления и проводимость линии:

=

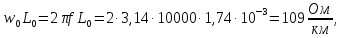
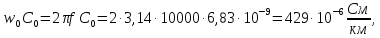
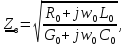
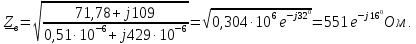
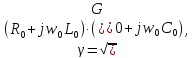
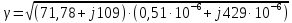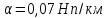- постоянная затухания;

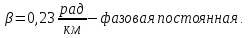
Вычислим

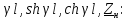
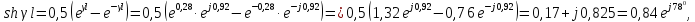
Определим напряжение и ток :

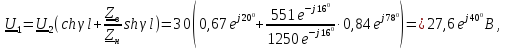
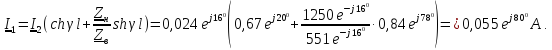
3. Вычислим активную и полную мощности в начале 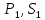и в конце линии 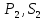, а также КПД линии:

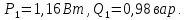
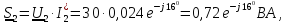
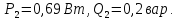
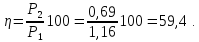
Полагая, что линия стала без потерь 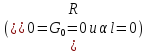, а нагрузка в конце линии стала активной и равна модулю комплексной нагрузки.

Определим напряжение 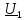и ток , а также длину электромагнитной волны λ.

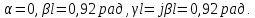
В уравнениях линии без потерь гиперболические функции заменяются тригонометрическими:

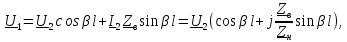
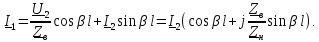
Нагрузка в конце линии:

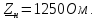
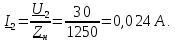
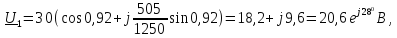
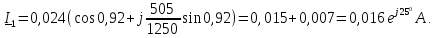
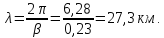
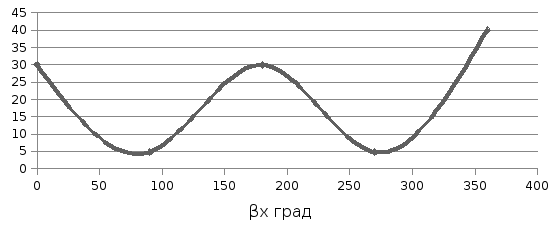
3 Для линии без потерь построим график распределения действующего значения напряжения вдоль линии в функции координаты Х.

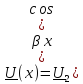
где

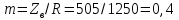
Расчеты сведем в таблицу:

0	0	1	0	0	30,0
λ/4	π/2	0	1	0,16	4,8
λ/2	π	1	0	0	30,0
3λ/4	3π/2	0	1	0,16	4,8
λ	2π	1	0	0	30,0