ДЗ первый курс / Метод наименьших квадратов + задания 2015

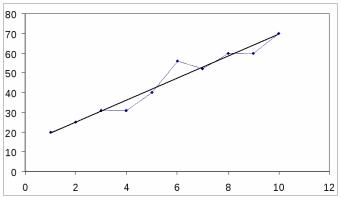
§ 1. КРАТКАЯ ТЕОРИЯ.

1.1. Постановка задачи.

В естествознании, биологии, экономике и других науках при измерении и наблюдении устанавливаются различные зависимости (связь между наблюдаемыми величинами X и У). Эти зависимости обычно выражают аналитически, т.е. различными формулами.

Формулы, составленные на основе данных, полученных в результате наблюдений, называются

Эмпирическими формулами.

Процесс получения эмпирических формул состоит из двух этапов:

1.Подбор вида элементарной функции;

2.Вычисление параметров этой функции.

Рассмотрим один из методов получения эмпирических формул - способ наименьших квадратов.

Пусть на основании эксперимента необходимо найти функциональную зависимость между переменными величинами Х и У.

По результатам измерений составим следующую таблицу:

Таблица 1.

Если вид функциональной зависимости неизвестен, то обычно поступают так: упорядоченные пары чисел (хi, yi) (i= 1,2,3 ...k) данной таблицы рассматривают как точки в прямоугольной системе координат ХОУ и строят график. Полученные точки будут группироваться около какой-то линии.

1.2. Выравнивание по прямой.

Предположим, что точки (хiуi) группируются около некоторой прямой.

рис 1.

В этом случае между переменными X и У существует функциональная зависимость, близкая к линейной. Будем искать эту зависимость в виде:

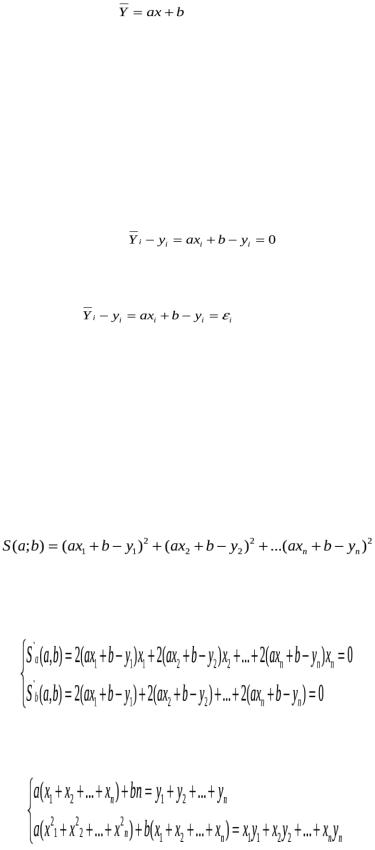
(1.1)

где a и b – параметры, подлежащие, вычислению,

- теоретическое значение функции (вычисленное по формуле).

Поставим задачу: найти такие значения а и b, чтобы прямая (1.1.) «наилучшим образом» проходила через множество точек Мi(xi,yi).

Если бы все точки Mi(xi,yi) лежали строго на прямой (1.1), то для каждой из точек было бы справедливо следующее равенство:

однако на практике имеет место следующее равенство:

(1.2)

т.е существует i (отклонение) между наблюдаемыми ординатами (эмпирическими) и ординатами, полученными по уравнению (теоретическими).

Принцип метода наименьших квадратов утверждает: оптимальны такие значения параметров а и b при которых сумма квадратов отклонений минимальна. Составим эту сумму:

или

(1.3)

Для исследования функции (1.3) с двумя переменными на минимум, найдем частные производные, приравняем их к нулю и решив систему уравнений, найдем а и b.

(1.4)

или

(1 .5)

Введя сокращенные обозначения, получим систему уравнений (1.5) в следующем виде:

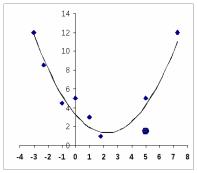
(1.6 )

Решив систему (1.6), найдем значения параметров а и bи подставим их значения в эмпирическую формулу (1.1).

Нахождение линейной функциональной зависимости называется выравнивание по прямой, а система уравнений (1.6) -нормальной системой метода наименьших квадратов при выравнивании по прямой.

1.3. Выравнивание по параболе.

Пусть точки Мi(xi,yi), соответствующее парам чисел таблицы 1, группируются вблизи некоторой параболы (рис 2).

рис 2.

В этом случае между переменными Х и У существует функциональная зависимость, которую будем искать в виде:

(1.7)

Найдем параметры a, b и c с таким расчетом, чтобы парабола заданная уравнением (1.7) «наилучшим образом» проходила через множество точек Мi(xi,yi), т.е чтобы сумма квадратов отклонений теоретических ординат точек от эмпирических была наименьшей.

Составим эту сумму:

(1.8)

Найдем частные производные по переменным a, b и c, приравняем их к нулю, преобразуем полученные уравнения и получим следующую систему уравнений:

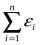
(1.9)

Система уравнений (1.9) называется нормальной системой метода наименьших квадратов при выравнивании по параболе.

Решив систему уравнений, найдем параметры a, b, c и подставим их значения в уравнение (1.7). Получим искомую эмпирическую функцию.

Замечание I. Число уравнений нормальной системы уравнений (1.6) и (I..9) метода наименьших квадратов соответствует числу искомых параметров.

Замечание 2. Между переменными х и у , заданными таблицей, существуют зависимости, близкие, например, к показательной функции вида у= аbx или у = lgy, у = lga+xlgb; к функции y=a/x+b (уравнение гиперболы) и др

§2. Порядок выполнения задания

1.Определить вид эмпирической формулы, используя данные задания (см.§1, п.2,3).

2.Написать нормальную систему уравнений (см.§1, п.2,3) в общем виде.

3.Для определения параметров выбранной эмпирической формулы составить расчетную таблицу (см § З).

4.Составить конкретную систему уравнений и решить ее любым способом.

5.Найти значение функции для значения X, выходящего за пределы таблицы (найти прогнозную оценку). Найти

6.Пояснить содержательный смысл коэффициента а, для линейной зависимости.

7.Построить в одной системе координат график полученной функции и точки по исходным данным. Наглядно убедиться, насколько хорошо теоретическая линия согласуется с эмпирической линией.

§3. Образец выполнения задания

Задание I. Имеются данные о назначенной месячной пенсии (руб) за последние девять месяцев 2014 года по РФ.

Таблица № 2

4.Решим систему методом подстановки, вычислим параметры a, b с точностью до 0,1.

или по правилу Крамера:

5. Подставляя найденные значения параметров в формулу, получим эмпирическую формулу:

(3.2)

выражающую зависимость между начисленной месячной пенсии и месяца года.

6. Используя формулу (3.2), можем найти теоретические значения У для данных значений Х и отклонение теоретической ординаты от эмпирической:

Сумма отклонений εi должна быть близкой к 0.

9

i ( 0.18)2 (0.14)2 (0.06)2 (0.08)2 02 (0.02)2 ( 0.01)2 02 ( 0.02)2 0.063

i1

С помощью формулы можно найти значения У для тех значений X, которое не содержатся в таблице, но взяты из области изменения X (интерполировать). Этот факт и оправдывает отыскание эмпирических формул.

Например, пусть Х=4,5, тогда У=0,02*4,5+1,5=1,59.

Отсюда, ух=4,5= 1,59 т.е. в середине апреля, будет назначена месячная пенсия в размере 1,59 тыс.руб.

Можно найти значение функции для значения X, выходящего за пределы таблицы, (экстраполировать), т.е. находить прогнозную оценку.

Например, при х=10, У=0,02*10+1,5=1,7, т.е. в октябре будет назначена месячная пенсия в размере 1,7 тыс.руб.

7. Выясним содержательный смысл параметров полученного уравнения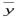=0,02х+1,5.

Коэффициент, а =0,02 определяет средний показатель увеличения месячной пенсии. С каждым месяцем начисленная месячная пенсия увеличивается в среднем на 0,02 тыс.руб.

Свободный член b=1,5 конкретного содержательного смысла не имеет, он определяет начальный уровень.

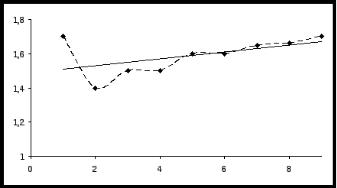
Наглядно убедимся в том, насколько хорошо теоретическая кривая согласуется с исходными данными. Для этого построим точки с координатами: (1;1,7); (2,1,4); (3,1,5); (4;1,5); (5,1,6); .(6,1,6); (7;1,65); (8;1,66); (9;1,7) и полученную теоретическую прямую по точкам

(0;1,5); (2;1,54) (рис.4).

На рисунке видно, что погрешности (отклонения εi) теоретических ординат от эмпирических малы по абсолютной величине. Следовательно, теоретическая функция хорошо согласуется с исходными данными.

Рис. 4

3.1. Замечание. Метод наименьших квадратов в обработке рядов динамики.

Статистика изучает социально-экономические явления не только в их взаимной связи и взаимной обусловленности, но и в движении, развитии.

Процесс развития социально-экономических явлений во времени в статистике называется динамикой.

Размеры отдельных социально-экономических явлений связанные с определенным периодом или датой времени, называют уровнями. Последовательности уровней образуют ряд динамики.

Формирование уровней ряда динамики происходит под воздействием многочисленных факторов, однако все действующие факторы можно подразделить на две группы:

1.Управляемые, регулируемые обществом факторы интенсификации производства.

2.Случайные, не поддающиеся контролю и регулированию факторы. Эта группа факторов вызывает случайные колебания и затушевывает основную тенденцию развития.

Первая группа факторов систематически действует в одном направлении и определяет характер долговременной тенденции ряда.

Для выявления основной тенденции развития ряда используется метод наименьших квадратов.

В социально-экономической статистике для выявления и аналитического выражения тенденции динамического ряда наиболее часто используются следующие функции: У=ax+b- линейная функция;

Y=ax2+bx+c- квадратичная функция; Y=abx- показательная функция.

Форму кривой, как обычно, определяют по графику ряда. Затем определяют параметры выбранной функции, решая систему нормальных уравнений вида (1.6) или (1.9) и находят эмпирическую функцию. По найденной эмпирической функции с определенной осторожностью можно получать прогнозные оценки на будущий период (экстраполировать) при условии, что период прогноза небольшой.

Практика показывает, что для большинства рядов динамики экономических явлений вполне удовлетворительные результаты дает выравнивание по прямой линии, особенно при использовании выводов для получения прогнозных оценок. Показательная кривая и парабола приводят, как правило, к завышенным оценкам.

§ 4. Варианты для самостоятельной работы.

Задание: Данные опыта представлены таблицей значений Х и У. Подобрать формулу эмпирической зависимости между Х и У. Найти параметры этой зависимости методом наименьших квадратов.

Вариант 1.Зависимость между нагрузкой У (кг) и сжатием X(мм) буферной пружины:

Вариант 2.Разрежение У (см. столба бензина) связано с расходом X топлива (см/мин).

Вариант 3.Температура Х (С°) смазочного масла в двигателе связана с температурой У (С0) смазочного масла в коробке передач.

Вариант 4.зависимость температур Х охлаждающегося тела от времени Т.

Вариант 5. Зависимость числа Х (об/мин) оборотов двигателя и мощности двигателя У (кВт)

Вариант 6.Время непрерывной работы У (час) электроприборов зависит от расхода электроэнергии (кВт/сек)

Вариант 7.Температура У (С0) смазочного масла в двигателе зависит от скорости Х (км/час) движения автомобиля.

Вариант 8. Износ лемеха У (мм) зависит от твердости Х (нрс) материала лемеха.

Вариант 9. Мощность двигателя У (кВт) связана с температурой Х (С0) воздуха.

Вариант 10. Вибрация У автомобиля зависит от скорости Х (км/час) движения.

Вариант 11. Прогиб балки У (м) связана с нагрузкой Х (кН).

Вариант 12.Электрические сопротивление R(Ом) проволоки зависит от температуры t(С0).

Вариант 13.Дана таблица удельного сопротивления (кн/м2) и производительности У (га/ч) посевного агрегата..

Вариант 14. Результаты измерений длительности Х (час) непрерывной работы двигателя и расхода У (л) топлива задана следующей таблицей.

Вариант 15.Скорость У охлаждения тела зависит от разности Х температуры и окружающей среды.

Вариант 16. Известны твердость Х ( кг/см2) почвы и износ У (мм) лемеха.

Вариант 17. Крутящий момент У (кг/см) зависит от угла кручения Х (рад).

Вариант 18. Стационарное распределение температуры в теплоизолированном тонком стержне задано таблицей значений измеренных температур У в соответствующих точках Х.