
- •Тема 1.3. Интерполяция функций
- •1.3.1. Постановка задачи
- •1.3.2. Интерполяционная формула Лагранжа
- •1.3.3. Интерполяционные формулы Ньютона
- •1.3.3.1. Конечные разности
- •1.3.3.2. Первая интерполяционная формула Ньютона
- •1.3.3.3. Вторая интерполяционная формула Ньютона
- •1.3.4. Сплайн – интерполяция
- •1.3.5. Сравнение интерполяционных многочленов по применению
- •1.3.6. Тестовые задания по теме «Интерполяция функций»
- •Тема 1.3. Интерполяция функций Страница 54
1.3.5. Сравнение интерполяционных многочленов по применению
Интерполяционные многочлены Лагранжа и Ньютонапредназначены для получения приближенной аналитической записи функции, заданной таблично.
Формулу Лагранжа можно применять для таблиц с различными расстояниями между узлами, а формулы Ньютона – только для таблиц с равноотстоящими узлами.
Формулы Ньютона имеют следующее преимущество перед формулой Лагранжа. Увеличение степени интерполяционного полинома на единицу (добавление в таблицу значений функции одного узла) при использовании формулы Лагранжа ведет не только к увеличению числа слагаемых, но и к необходимости пересчета каждого коэффициента заново, тогда как при использовании формулы Ньютона достаточно добавить к уже существующему многочлену только одно слагаемое.
В сравнении с рассмотренными методами большую точность интерполяции можно получить применением методов сплайн –интерполяции.
1.3.6. Тестовые задания по теме «Интерполяция функций»
Задача замены таблично заданной функции y = f(x) другой функцией g(x), такой, что g(xi) = f(xi) (i = 0, 1, 2, … n), это
задача интерполяции
задача аппроксимации
решение уравнения
задача оптимизации
Узлы интерполяции – это
значения функции, заданной таблично
значения xi (i = 0, 1, 2, … n)
значения интерполяционного многочлена в точках xi (i = 0, 1, 2, … n)
в списке нет правильного ответа
Шаг интерполяции – это
шаг интегрирования
разность между соседними значениями функции
расстояние между узлами интерполяции
в списке нет правильного ответа
Основное условие интерполяции – это
совпадение значений интерполируемой и интерполирующих функций во всех узлах интерполяции с заданной степенью точности
значения интерполируемой и интерполирующих функций в узлах интерполяции не должны совпадать
в списке нет правильного ответа
полное совпадение значений интерполируемой и интерполирующих функций во всех узлах интерполяции
Связь между числом узлов интерполяции и степенью интерполяционного многочлена следующая
степень интерполяционного многочлена на единицу меньше числа узлов
степень интерполяционного многочлена не зависит от числа узлов
степень многочлена равна числу узлов
в списке нет правильного ответа
Если точка интерполяции Х находится в начале таблицы с равноотстоящими узлами, то для построения интерполяционного полинома с возможно меньшей погрешностью используется
формула Лагранжа
первая формула Ньютона
формула Симпсона
вторая формула Ньютона
Изменение степени интерполяционного полинома на единицу (добавление в таблицу значений функции одного узла) ведет к полному пересчету
первой формулы Ньютона
второй формулы Ньютона
формулы Лагранжа
нет правильного ответа
Вторая интерполяционная формула Ньютона используется, когда точка интерполяции находится
в начале таблицы с равноотстоящими узлами
в середине таблицы с равноотстоящими узлами
все ответы верные
в конце таблицы с равноотстоящими узлами
При использовании n + 1 узла таблицы интерполяционный полином Лагранжа является полиномом
n–ой степени
n – 1–ой степени
n + 2–ой степени
в списке нет правильного ответа
Если интерполируемая функция f(x) задана в (n + 1) равноотстоящих узлах, то для ее интерполяции удобнее использовать
формулу Ньютона
формулу Лагранжа
формулу Симпсона
в списке нет правильного ответа
Универсальность формулы Лагранжа заключается в возможности
нахождения значений функции как в начале, так и в конце таблицы
все ответы верные
нахождения значений функции в любом месте таблицы
ее использования для случая неравноотстоящих узлов
Точность интерполяции зависит
от величины шага интерполяции
от выбранного метода
в списке нет правильного ответа
Интерполяционная формула Лагранжа относится к классу
показательных функций
тригонометрических функций
полиноминальных функций
экспоненциальных функций
При использовании интерполяционных формул Ньютона располагать узлы в произвольном порядке
нельзя
можно
можно, но только для первой формулы Ньютона
можно, но только для второй формулы Ньютона
Добавление очередного узла интерполяции при использовании формул Ньютона требует
полного пересчета формулы
пересчета только последнего слагаемого
в списке нет правильного ответа
вычисления дополнительного слагаемого
При построении линейного интерполяционного многочлена Лагранжа
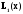 для
функции, заданной таблично, значение
функции в точкех=0.18,
равно
для
функции, заданной таблично, значение
функции в точкех=0.18,
равно
|
х |
0.1 |
0.15 |
0.2 |
|
у |
-1 |
-0.7 |
-0.5 |
 -0.48
-0.48 -0.58
-0.58 0.68
0.68формулу Лагранжа использовать нельзя
При построении линейного интерполяционного многочлена Ньютона Р1(х) для функции, заданной таблично, значение функции в точке х=0.11
|
х |
0.1 |
0.2 |
0.3 |
|
у |
0.8 |
0.5 |
0.6 |
 -0.752
-0.752 0.568
0.568Формулу Ньютона использовать нельзя.
 0.77
0.77
При построении линейного интерполяционного многочлена Лагранжа
 для
функции, заданной таблично, значение
функции в точкех=2.5
равно
для
функции, заданной таблично, значение
функции в точкех=2.5
равно
|
x |
0 |
2 |
4 |
|
f(x) |
1.7 |
1.9 |
2.5 |
 2.99
2.99 3.61
3.61 2.05
2.05
 4.16
4.16
При построении линейного интерполяционного многочлена Лагранжа
 для
функции, заданной таблично, значение
функции в точкех=0.25
равно
для
функции, заданной таблично, значение
функции в точкех=0.25
равно
|
x |
0.2 |
0.3 |
0.6 |
|
f(x) |
4.5 |
5.0 |
7.6 |
 4.75
4.75
 1.00
1.00 5.61
5.61 6.16
6.16
При построении линейного интерполяционного многочлена Ньютона Р1(х) для функции, заданной таблично, значение функции в точке х=0.41 равно
|
x |
0.4 |
0.5 |
0.6 |
|
f(x) |
0.6 |
0.55 |
0.65 |
 0.575
0.575
 1.75
1.75 0.58
0.58 0.12
0.12
При построении интерполяционного многочлена Лагранжа
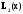 значение
функции, заданной таблично, значение
функции в точкех=0.12,
равно
значение
функции, заданной таблично, значение
функции в точкех=0.12,
равно
|
х |
0.1 |
0.15 |
0,2 |
|
у |
-1 |
-07 |
-0.5 |
 -0.418
-0.418 0.618
0.618 -0.868
-0.868
формулу Лагранжа использовать нельзя
При построении интерполяционного многочлена Ньютона Р2(х) для функции, заданной таблично, значение функции в точке х=0.11
|
х |
0.1 |
0.2 |
0.3 |
|
у |
0.8 |
0.5 |
0.6 |
 -0.752
-0.752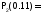 0.752
0.752 0.568
0.568Формулу Ньютона использовать нельзя
При построении интерполяционного многочлена Ньютона Р2(х) для функции, заданной таблично, значение функции в точке х=1.8 равно
|
х |
1 |
2 |
3 |
|
у |
2.2 |
5.2 |
8.4 |
 4.728
4.728
 -0.752
-0.752 1.568
1.568Формулу Ньютона использовать нельзя
При построении интерполяционного многочлена Лагранжа
 для функции, заданной таблично, значение
в точкех=3.6
равно
для функции, заданной таблично, значение
в точкех=3.6
равно
|
х |
3 |
4 |
5 |
|
у |
5.2 |
8.4 |
10.5 |
 8.654
8.654 7.252
7.252
 7.561
7.561 4.675
4.675
При построении интерполяционного многочлена Ньютона Р2(х) для функции, заданной таблично, значение функции в точке х=4.2 равно
|
х |
4 |
4.5 |
6 |
|
у |
5.3 |
8.2 |
11.4 |
Формулу Ньютона использовать нельзя
 8.752
8.752 9.568
9.568 1.3
1.3
Погрешность в точке х=4.5 при замене функции
 интерполяционным многочленом первой
степени, построенным по узлам
интерполяционным многочленом первой
степени, построенным по узлам и
и ,
равна
,
равна
0.775
1.158
1.412
0.003
Приближенное значение функции
 в точкех=1.5,
вычисленное с использованием
интерполяционного многочлена Ньютона
по узлам
в точкех=1.5,
вычисленное с использованием
интерполяционного многочлена Ньютона
по узлам
 и
и ,
равно
,
равно
 3.5
3.5
 2.75
2.75 6.58
6.58 7.12
7.12
Приближенное значение функции
 в точкех=1.5,
вычисленное с использованием
интерполяционного многочлена Лагранжа
по узлам
в точкех=1.5,
вычисленное с использованием
интерполяционного многочлена Лагранжа
по узлам
 и
и ,
равно
,
равно
 2.175
2.175 3.58
3.58 5.053
5.053
 7.12
7.12
Погрешность в точке х=1.5 при замене функции
 интерполяционным многочленом первой
степени, построенным по узлам
интерполяционным многочленом первой
степени, построенным по узлам и
и ,
равна
,
равна
1.125
2.775
0.158
0.412
