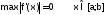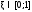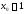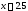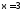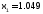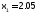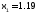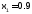- •Тема 1.2. Методы решения нелинейных уравнений
- •1.2.2. Отделение корней
- •1.2.2.1. Графическое отделение корней
- •1.2.2.2. Аналитическое отделение корней
- •1.2.3. Уточнение корней
- •1.2.3.1. Метод половинного деления
- •1.2.3.2. Метод итерации
- •1.2.3.3. Метод Ньютона (метод касательных)
- •1.2.3.4. Метод хорд
- •1.2.3.5. Сравнение методов решения нелинейных уравнений
- •1.2.4. Тестовые задания по теме «Методы решения нелинейных уравнений»
- •Тема 1.2 Методы решения нелинейных уравнений Страница 36
1.2.3.5. Сравнение методов решения нелинейных уравнений
Метод половинного деленияочень прост и имеет одно явное преимущество по сравнению со всеми рассмотренными выше методами – он всегда сходится. Однако, скорость сходимости очень мала, поэтому его часто используют для грубого уточнения корня.
Метод касательных(метод Ньютона) эффективен для решения уравнений, график которых в окрестности корня имеет большую крутизну. Метод обладает высокой скоростью сходимости, но его сходимость зависит от вида функции, поэтому рекомендуется отрезок, на котором отделяется корень, выбирать очень небольшой длины.
Метод хорд,являясь модификацией метода касательных, также обладает хорошей скоростью сходимости. При правильном выборе неподвижной точки последовательность приближений гарантированно сходится к корню уравнения.
Метод простой итерациидает возможность «угадывать» новые значенияхна любом шаге. Следовательно, если процесс сходится медленно, можно вносить коррективы, учитывая предыдущие результаты. Метод прост и обладает хорошей сходимостью. Однако перед его использованием требуется преобразование исходного уравнения и проведение дополнительных вычислений.
Отметим, что на практике при решении нелинейных уравнений обычно используется комбинация нескольких методов.
1.2.4. Тестовые задания по теме «Методы решения нелинейных уравнений»
Нелинейное уравнение – это
алгебраическое или трансцендентное уравнение
алгебраическое уравнение
тригонометрическое уравнение
трансцендентное уравнение
Нахождение возможно более узкого отрезка, содержащего только один корень уравнения, называется
разделением корней
отделением корней
уточнением корней
решением нелинейного уравнения
На отрезке [a;b] имеется хотя бы один корень, если
Этапы решения нелинейного уравнения называются
отделение корней и уточнение отделенного корня
графическое и аналитическое вычисления корня
табличное отделение корня и аналитическое уточнение корня
вычисления каждого из корней уравнения
Начальное приближение к корню это
значение х, при котором уравнение обращается в тождество
значение х, принадлежащее отрезку, содержащему корень
значение х, являющееся одним из концов отрезка, содержащего корень
значение х, обеспечивающее сходимость метода уточнения корня
Чтобы выбрать x0 в качестве начального приближения в методе Ньютона, необходимо, чтобы в этой точке
функция и вторая производная имели одинаковые знаки
функция и первая производная имели одинаковые знаки
первая и вторая производная имели одинаковые знаки
функция и первая производная имели разные знаки
Метод решения нелинейного уравнения, в результате которого получается последовательность вложенных отрезков – это
метод итерации
метод половинного деления
метод Ньютона – Рафсона
метод хорд
в списке нет правильного ответа
Правилом выбора итерирующей функции при использовании метода итераций является
За начальное приближение в методе итерации принимают

 ,
если
,
если

в списке нет правильного ответа
 ,
если
,
если

Правилом выбора неподвижной точки при использовании метода хорд является



в списке нет правильного ответа
За начальное приближение в методе Ньютона выбирают конец отрезка, для которого



в списке нет правильного ответа
Метод Ньютона применять не рекомендуется, если
 -
выпуклая
-
выпуклая - монотонная
- монотонная -
пологая
-
пологаяв списке нет правильного ответа
Если на заданном отрезке имеется два корня, то о методе итераций можно сказать
метод обеспечит сходимость к одному из корней
метод разойдется
в списке нет правильного ответа
сходимость метода не гарантирована
В процессе решения уравнения методом простой итерации приближение к корню может осуществляться
монотонно или колебательно
монотонно со стороны начального приближения
колебательно справа и слева от корня
в списке нет правильного ответа
Метод решения нелинейного уравнения, обладающий свойством "самокоррекции"
метод хорд
метод итераций
метод Ньютона-Рафсона
метод Вегстейна
Корень уравнения
 принадлежит отрезку
принадлежит отрезку
Корень уравнения
 принадлежит отрезку
принадлежит отрезку
Корень уравнения
 принадлежит отрезку
принадлежит отрезку
Корень уравнения
 принадлежит отрезку
принадлежит отрезку
Корень уравнения
 принадлежит отрезку
принадлежит отрезку
Начальным приближением к корню при решении уравнения
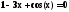
 методом половинного деления служит
методом половинного деления служит
Начальным приближением к корню при решении уравнения

 методом
простой итерации служит
методом
простой итерации служит
любое значение




Начальным приближением к корню при решении уравнения
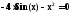
 методом
Ньютона служит
методом
Ньютона служит



любое значение

Начальным приближением к корню при решении уравнения

 методом хорд
служит
методом хорд
служит



любое значение

Неподвижной точкой при решении уравнения
 ,
если корень отделен на отрезке
,
если корень отделен на отрезке ,
служит
,
служит
При решении уравнения

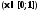 методом половинного деления с заданной
точностью
методом половинного деления с заданной
точностью требуется
выполнить
требуется
выполнить
7 итераций
6 итераций
5 итераций
4 итерации
При решении уравнения

 методом половинного деления погрешность
результата после трех итераций равна
методом половинного деления погрешность
результата после трех итераций равна
0.25
0.125
0.625
0.01
Первым приближением к корню при решении уравнения

 методом
Ньютона, если
методом
Ньютона, если ,
является
,
является
Первым приближением к корню при решении уравнения

 методом хорд, если
методом хорд, если ,
является
,
является
Первым приближением к корню при решении уравнения
 методом итераций, если
методом итераций, если ,
является
,
является