- •Тема 1.5. Методы решения обыкновенных дифференциальных уравнений
- •1.5.2. Метод Эйлера
- •1.5.3. Методы Рунге-Кутты
- •1.5.4. Решение оду n-го порядка
- •1.5.5. Сравнение методов решения оду
- •1.5.7. Тестовые задания по теме «Методы решения обыкновенных дифференциальных уравнений»
- •Тема 1.5. Методы решения обыкновенных дифференциальных уравнений Страница 84
1.5.7. Тестовые задания по теме «Методы решения обыкновенных дифференциальных уравнений»
Обыкновенное дифференциальное уравнение – это
дифференциальное уравнение от одной переменной
дифференциальное уравнение первого порядка
дифференциальное уравнение n-ого порядка
в списке нет правильного ответа
Порядок ОДУ это
количество производных, входящих в состав уравнения
наивысший порядок производной, входящей в состав уравнения
количество неизвестных, входящих в состав ОДУ
в списке нет правильного ответа
Общим решением ОДУ
 является
является

таблица значений искомой функции

в списке нет правильного ответа
Частным решением ОДУ
 является
является

таблица значений искомой функции
в списке нет правильного ответа

Численным решением ОДУ
 является
является

таблица значений искомой функции

в списке нет правильного ответа
 -
эта формула используется для определения
очередного значения функции по методу
-
эта формула используется для определения
очередного значения функции по методу
Рунге-Кутты 2-го порядка
Рунге-Кутты 4-го порядка
Рунге-Кутты 1-го порядка
в списке нет правильного ответа
Уменьшение шага интегрирования при использовании методов Рунге-Кутты
увеличивает погрешность
не влияет на погрешность
в списке нет правильного ответа
уменьшает погрешность
Очередная точка решения ОДУ методом Рунге-Кутты вычисляется на основании
одного предыдущего значения функции
двух предыдущих значений функции
трех предыдущих значений функции
всех предыдущих значений функции
Применение переменного шага является
невозможным в методах Рунге-Кутты
возможным во всех методах Рунге-Кутты
возможным только в методе Рунге-Кутты 4-го порядка
возможным только в методе Эйлера
Погрешность метода Эйлера пропорциональна
шагу
шагу, возведенному в куб
шагу, возведенному в квадрат
двум шагам
Чтобы применить методы Рунге-Кутты при решении ОДУ 2-го порядка нужно
привести ОДУ 2-го порядка к ОДУ 1-го порядка
иметь информацию о двух начальных точках решения
в списке нет правильного ответа
привести ОДУ 2-го порядка к системе ОДУ 1-го порядка
В формуле оценки погрешности при использовании метода автоматического выбора шага порядок используемого метода Рунге-Кутты
учитывается с помощью коэффициента, равного порядку метода
учитывается в расчетных формулах используемого метода
не учитывается
в списке нет правильного ответа
Для увеличения точности решения ОДУ количество итераций в методе автоматического выбора шага
увеличивается
уменьшается
не меняется
накапливается
Не зная точного решения, оценить погрешность решения ОДУ
все ответы верны
можно с использованием правила Рунге
можно с использованием метода автоматического выбора шага
можно с использованием метода двойного просчета
Метод решения ОДУ, в котором подынтегральная функция на отрезке аппроксимируется интерполяционным многочленом 1-го порядка, а затем интегрируется методом прямоугольников, это
метод Рунге-Кутты 3-го порядка
метод Эйлера
модифицированный метод Эйлера
метод Рунге-Кутты 4-го порядка
Решением ОДУ
 с начальными условиями
с начальными условиями методом Эйлера на отрезке[0;0.4]
с шагом
методом Эйлера на отрезке[0;0.4]
с шагом
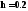 является:
является:
Решением ОДУ
 с начальными условиями
с начальными условиями методом Эйлера на отрезке[0;0.4]
с шагом
методом Эйлера на отрезке[0;0.4]
с шагом
 является
является
Решением ОДУ
 с начальными условиями
с начальными условиями методом Эйлера на отрезке[0;1]
с шагом
методом Эйлера на отрезке[0;1]
с шагом
 является
является
Решением ОДУ
 с начальными условиями
с начальными условиями методом Эйлера на отрезке[0;2]
с шагом
методом Эйлера на отрезке[0;2]
с шагом
 является
является
Решением ОДУ
 с начальными условиями
с начальными условиями методом Рунге- Кутты 2-го порядка в
точкех=0.2
является
методом Рунге- Кутты 2-го порядка в
точкех=0.2
является
 2.98
2.98 0.87
0.87 3.89
3.89 1.24
1.24
Решением ОДУ
 с начальными условиями
с начальными условиями методом Рунге -Кутты 2-го порядка в точкех=0.3
является
методом Рунге -Кутты 2-го порядка в точкех=0.3
является
 0.045
0.045
 0.9
0.9 -0.78
-0.78 0
0
Решением ОДУ
 с начальными условиями
с начальными условиями методом Рунге-Кутты 2-го порядка в точкех=0.1
является
методом Рунге-Кутты 2-го порядка в точкех=0.1
является
 1.98
1.98 1.005
1.005 3.56
3.56 4.67
4.67
Решением ОДУ
 с начальными условиями
с начальными условиями методом Рунге- Кутты 2-го порядка в точке
х=0.1 является
методом Рунге- Кутты 2-го порядка в точке
х=0.1 является
 2.56
2.56 8.48
8.48 1.121
1.121 2.75
2.75
Решением ОДУ
 с начальными условиями
с начальными условиями методом Рунге- Кутты 2-го порядка в точкех=0.5
является
методом Рунге- Кутты 2-го порядка в точкех=0.5
является
 3.001
3.001 2.142
2.142 4.145
4.145 1.781
1.781
Значение погрешности в точке х=0.5 при решении ОДУ
 с начальными условиями
с начальными условиями (h=0.5) методом Эйлера, равно
(h=0.5) методом Эйлера, равно
0.149
0.001
0.780
1.765
Решением ОДУ
 с начальными условиями
с начальными условиями методом Рунге- Кутты 4-го порядка в
точкех=0.5
является
методом Рунге- Кутты 4-го порядка в
точкех=0.5
является
 1.797
1.797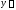 0.454
0.454 1.001
1.001 0.965
0.965
Решением ОДУ
 с начальными условиями
с начальными условиями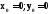 методом Рунге Кутты 4-го порядка в точкех=0.3
является
методом Рунге Кутты 4-го порядка в точкех=0.3
является
 0
0 0.045
0.045
 1
1 2.876
2.876
Решением ОДУ
 с начальными условиями
с начальными условиями методом Рунге-Кутты 4-го порядка в
точкех=0.5
является
методом Рунге-Кутты 4-го порядка в
точкех=0.5
является
 2.5
2.5 3.015
3.015 1.016
1.016
 -1.5
-1.5
Решением ОДУ
 с начальными условиями
с начальными условиями методом Рунге-Кутты 4-го порядка в точкех=2.1
является
методом Рунге-Кутты 4-го порядка в точкех=2.1
является
 3.1
3.1 1.2
1.2 4.2
4.2 2.1
2.1
Решением ОДУ
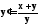 с начальными условиями
с начальными условиями методом Рунге- Кутты 4-го порядка в
точкех=1.5
является
методом Рунге- Кутты 4-го порядка в
точкех=1.5
является
 2.762
2.762 0.786
0.786 1.760
1.760 4.654
4.654