
Литература / Лекции С.А.Попов / Tema_7_Bak_chetyrekh
.doc
ТЕМА 7_Бак |
многополюсные цепи |
7. Основы теории четырехполюсников7.1. Уравнения четырехполюсника 7.2. Коэффициенты четырехполюсника 7.3. Эквивалентные схемы 7.4. Характеристические параметры четырехполюсника
|
7. Основы теории четырехполюсников
ОСНОВНЫЕ ПОНЯТИЯ
Четырехполюсник – часть электрической цепи, имеющая два входных и два выходных зажима (трансформатор, линия электропередачи, фильтр, электронный усилитель).
Понятием "четырехполюсник" пользуются, когда нужно знать токи и напряжения на входе и выходе электротехнического устройства и нет необходимости знать токи и напряжения внутри этого устройства.

Пассивный четырехполюсник – четырехполюсник не содержит источника энергии (активный – содержит).
Симметричный четырехполюсник – перемена местами его входных и выходных зажимов не изменяет входных и выходных напряжений и токов.
7.1. Уравнения четырехполюсника
Связь между напряжениями и токами на входе и выходе четырехполюсника (Ú1, İ1, Ú2, İ2) выражается с помощью двух уравнений четырехполюсника, в которых по двум заданным величинам находят две другие.
Всего можно записать шесть различных по форме, но по существу эквивалентных систем уравнений (число сочетаний из четырех по два).
![]() ,
,
![]() .
.
Этим уравнениям соответствуют определенные условно положительные направления токов и напряжений во входной и выходной цепях четырехполюсника.
Параметры (коэффициенты) четырехполюсника
(![]() )
зависят от структуры (схемы внутренних
соединений) четырехполюсника, величин
сопротивлений элементов, составляющих
четырехполюсник, и представляют в общем
случае комплексные числа.
)
зависят от структуры (схемы внутренних
соединений) четырехполюсника, величин
сопротивлений элементов, составляющих
четырехполюсник, и представляют в общем
случае комплексные числа.
Для каждого четырехполюсника эти коэффициенты можно определить расчетным или опытным путем.

 – тип (форма) А;
– тип (форма) А;
или
 – основное уравнение четырехполюсника.
– основное уравнение четырехполюсника.

 – тип B;
– тип B;
или

Уравнения связи между коэффициентами
![]() .
.
Для симметричного четырехполюсника
![]() .
.

 – Z - форма. Уравнение
связи
– Z - форма. Уравнение
связи
![]() .
.
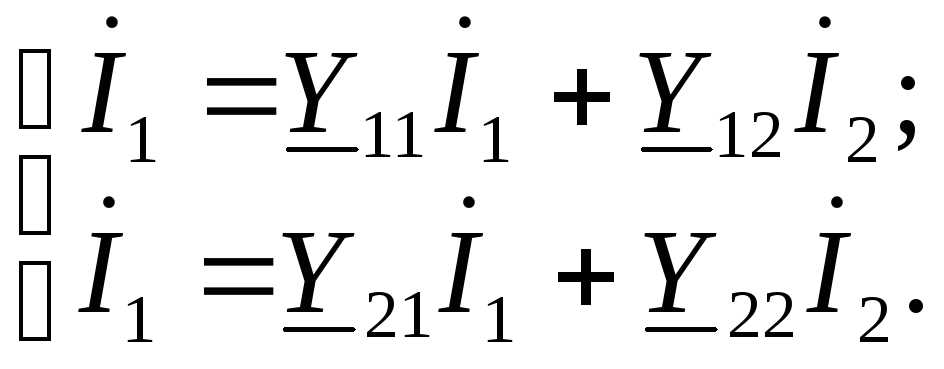 – Y - форма. Уравнение
связи
– Y - форма. Уравнение
связи
![]() .
.
 – H - форма. Уравнение
связи
– H - форма. Уравнение
связи
![]() .
.
 – G - форма. Уравнение
связи
– G - форма. Уравнение
связи
![]() .
.
Коэффициенты четырехполюсника для различных форм записи связаны между собой соотношениями, позволяющими переходить от одной формы записи уравнений к другой. Эти соотношения даются в справочниках. Поэтому достаточно установить значения коэффициентов и другие зависимости для одной формы записи и тогда можно получить все необходимые величины для любой другой формы записи.
В дальнейшем все необходимые соотношения будем рассматривать для А-формы записи уравнений.
Для записи уравнений четырехполюсника широко применяют матричную форму записи. Это особенно удобно и эффективно при исследовании режимов работы нескольких четырехполюсников, соединенных между собой тем или иным способом (каскадно, последовательно, параллельно и т. д.).
 или
или
![]() ;
;
 или
или
 .
.
7.2. Коэффициенты четырехполюсника
Четырехполюсник задан, если известны его коэффициенты.
Практически для расчета коэффициентов пользуются величинами входных сопротивлений четырехполюсника в режиме КЗ и ХХ.
Сопротивления ХХ и КЗ могут быть либо
измерены с помощью измерительного моста
или амперметра, вольтметра, ваттметра
и фазометра, включенных вначале со
стороны входа, а затем со стороны выхода
(обратное КХ и ХХ), либо вычислены
по известной схеме четырехполюсника.
Затем по полученным
![]() и
и
![]() определяют коэффициенты по известным
формулам.
определяют коэффициенты по известным
формулам.
ВХОДНЫЕ СОПРОТИВЛЕНИЯ
Со входа
![]() .
.
С выхода
![]() .
.
Для симметричного четырехполюсника
![]() ,
,
![]() .
.
При ХХ
![]() ;
;
![]() ,
,
![]() .
.
При КЗ
![]() ;
;
![]() ,
,
![]() .
.
Отсюда:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Легко показать, что
![]() ;
;
![]() .
.
Учитывая уравнение связи
![]() для вычисления 4-х коэффициентов надо
определить только 3 входных сопротивления.
для вычисления 4-х коэффициентов надо
определить только 3 входных сопротивления.
Для симметричного четырехполюсника
![]() ,
а потому достаточно знать только два
входных сопротивления (
,
а потому достаточно знать только два
входных сопротивления (![]() ,
,
![]() ).
).
 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
7.3. Эквивалентные схемы
Любой сложный четырехполюсник можно заменить простой схемой замещения.
Так как пассивный четырехполюсник характеризуется только тремя независимыми параметрами, то простейшая эквивалентная схема замещения четырехполюсника должна содержать 3 элемента: Т-образная и П-образная схема.


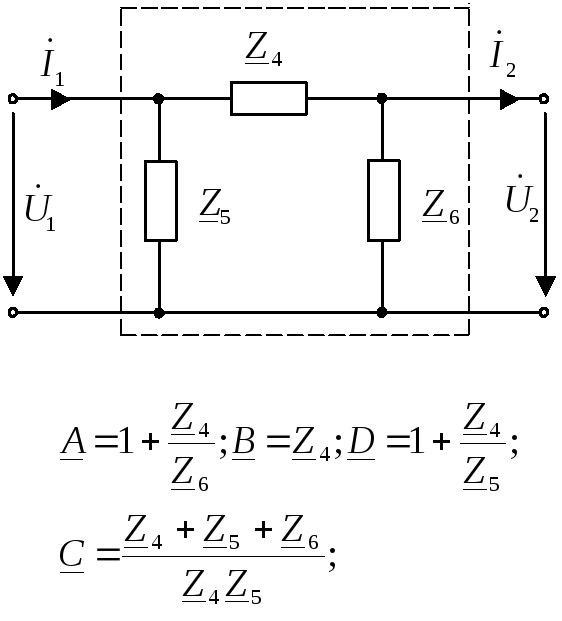
Для Т-образной схемы замещения:
![]() ;
;
![]() ;
;
![]() .
.
Для П-образной схемы замещения:
![]() ;
;
![]() ;
;
![]() .
.
Для симметричного четырехполюсника:
![]() ;
;
![]() .
.
7.4. Характеристические параметры четырехполюсника
При прохождении сигнала через четырехполюсник важно дать оценку изменения напряжения (тока) как по модулю, так и по фазе.
 ;
;
![]() ;
;
![]() ;
;
 ;
;
![]() ;
;
![]() .
.
Аналогично:
![]() .
.
В полученных выражениях ослабление по модулю и изменение фазы напряжения (тока) зависит как от обобщенных параметров (коэффициентов) четырехполюсника, так и от полного сопротивления нагрузки.
Для сравнения различных четырехполюсников с точки зрения прохождения через них сигналов желательно давать оценку только опираясь на коэффициенты четырехполюсника.
Для этого следует взять какую-либо определенную нагрузку и связать ее с коэффициентами четырехполюсника, т.е. сравнивать четырехполюсники следует при какой-то определенной нагрузке.
Известно, что входное сопротивление четырехполюсника:
![]() ;
;
![]() – для симметричного четырехполюсника.
– для симметричного четырехполюсника.
Для практики наибольший интерес
представляет согласованный режим
каскадно включенных симметричных
четырехполюсников. Для согласованного
режима надо подобрать
![]() .
Это сопротивление называется
характеристическим и обозначается:
.
Это сопротивление называется
характеристическим и обозначается:
![]() ;
;
тогда ![]() ,
отсюда
,
отсюда
![]() .
.
Условие согласования каскадов – входное сопротивление последующего каскада равно выходному сопротивлению предыдущего. При этом обеспечивается максимум передачи мощности.
Характеристическим называется сопротивление нагрузки симметричного четырехполюсника, обеспечивающее ему режим согласованной нагрузки.
Рассмотрим случай симметричного четырехполюсника:
![]() .
.
Режим симметричного четырехполюсника,
нагруженного на характеристическое
сопротивление (![]() )
называется режимом согласованной
нагрузки, так как в этом случае
входное сопротивление четырехполюсника
равно сопротивлению нагрузки и равно
)
называется режимом согласованной
нагрузки, так как в этом случае
входное сопротивление четырехполюсника
равно сопротивлению нагрузки и равно
![]() .
.
Для согласованного режима симметричного четырехполюсника
 ;
;
Аналогично:
![]() .
.
![]() – отношение представляет собой
комплексное число:
– отношение представляет собой
комплексное число:
![]() ,
,
где ![]() [безразмерная величина] – модуль
отношения напряжений (токов) на входе
и на выходе – показывает, во сколько
раз изменяется по модулю напряжение
(ток) при прохождении через четырехполюсник.
[безразмерная величина] – модуль
отношения напряжений (токов) на входе
и на выходе – показывает, во сколько
раз изменяется по модулю напряжение
(ток) при прохождении через четырехполюсник.
![]() – постоянная фазы четырехполюсника,
показывающая на сколько изменяется
фаза напряжения (тока) при прохождении
через четырехполюсник.
– постоянная фазы четырехполюсника,
показывающая на сколько изменяется
фаза напряжения (тока) при прохождении
через четырехполюсник.
Для оценки изменения напряжения (тока)
при прохождении через четырехполюсник
как по модулю, так и по фазе одной
величиной (!) заменяют
![]() .
.
Тогда
![]() ,
,
где ![]() – постоянная передачи четырехполюсника;
– постоянная передачи четырехполюсника;
![]() – постоянная ослабления.
– постоянная ослабления.
![]() – непер.
– непер.
|
|
1 |
2,72 |
10 |
100 |
1000 |
|
|
0 |
1 |
2,3 |
4,6 |
6,9 |
1 Нп – затухание, при котором
![]() .
.
Затухание в неперах:
![]() .
.
Затухание в белах [Б]:
![]() .
.
Затухание в децибелах [дБ]:
![]() .
.
![]() .
.
![]() и
и
![]() – характеристические параметры
симметричного четырехполюсника,
зависящие только от структуры и
параметров элементов четырехполюсника:
– характеристические параметры
симметричного четырехполюсника,
зависящие только от структуры и
параметров элементов четырехполюсника:
![]() ;
;
![]() или
или
![]() .
.
Если учесть, что
![]() ,
то можно выразить коэффициенты
симметричного четырехполюсника через
характеристические параметры:
,
то можно выразить коэффициенты
симметричного четырехполюсника через
характеристические параметры:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
 ;
;
![]() .
.
В результате преобразований получим:
![]() ;
;
![]() ;
;
![]() .
.
Тогда уравнения симметричного четырехполюсника в гиперболической форме записи:

Эти уравнения применимы при любой нагрузке и широко используются в теории фильтров и теории электрических цепей с распределенными параметрами.
В технических устройствах источник энергии (или сигналов) соединяют с приемником через цепь, состоящую из ряда четырехполюсников, соединенных каскадно, то есть входные зажимы каждого последующего четырехполюсника соединяют с выходными зажимами предыдущего.

В таких устройствах важно обеспечить максимум передачи мощности от источника к приемнику, то есть согласованный режим работы всех каскадов.
Условие согласования каскадов – входное сопротивление последующего каскада равно выходному сопротивлению предыдущего.

Рассмотрим наиболее интересный для практики случай симметричного четырехполюсника:
![]() .
.
Для четырехполюсника в А–форме:
 ;
;
![]() ;
;
![]() .
.
![]() – характеристическое (повторное)
сопротивление симметричного
четырехполюсника.
– характеристическое (повторное)
сопротивление симметричного
четырехполюсника.
Нагружая четырехполюсник на
![]() на входе четырехполюсника будет
сопротивление
на входе четырехполюсника будет
сопротивление
![]() .
.
Тогда
![]() .
.
Для режима согласованной нагрузки симметричного четырехполюсника:

