гидравлика для преподавателя

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Тольяттинский государственный университет Инженерно-строительный институт Кафедра «Водоснабжение и водоотведение»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к практическим занятиям по дисциплине «ГИДРАВЛИКА»

для преподавателя

Тольятти 2007

1

УДК 532.5

Методические указания к практическим занятиям по дисциплине «Гидравлика» для преподавателя (технология 30/70) / Составитель Калинин А.В., Лушкин И. А. – Тольятти: ТГУ, 2007.

Представлены основные законы покоя и движения жидкостей и газов, гидравлические сопротивления, основы моделирования гидромеханических явлений. Приведены практические задачи для решения на практических занятиях.

Ил. 15; табл. 13; библиогр.: 9 наим.

Составители: Калинин А.В., Лушкин И. А. Научный редактор: Вдовин Ю.И.

2

Оглавление

3

1. УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ

1.1. Основные свойства жидкостей и газов

Капельные жидкости обладают свойством текучести и мало изменяют объем под действием давления. Газы сжимаемы и легко меняют объем. Основными физическими характеристиками жидкостей и газов являются:

плотность: ρ = m кг , где т – масса жидкости в объеме V;3

V м

удельный вес: γ = G Н , где: G - вес жидкости;3

V м

сжимаемость, которая характеризуется коэффициентом объемного сжатия:

где V-первоначальный объем, V – изменение объема при изменении давления р;

вязкость – способность жидкости оказывать сопротивление относительному сдвигу ее частиц. Вязкость влияет на величину касательного напряжения трения:

τ = μ dudy ,

где μ - динамическая вязкость (Па с); dudy – градиент скорости.

Динамическая вязкость μ связана с кинематической вязкостью ν соотношением:

μ = ν ρ.

1.2. Гидростатика

Основное уравнение гидростатики определяет величину гидростатического давления р в любой точке жидкости, если на жидкость из всех массовых сил действует только сила тяжести

р = p0 + ρgh ,

где р0 – давление на какой-либо поверхности уровня жидкости, например на свободной поверхности (Па), h – глубина расположения рассматриваемой точки от поверхности с давлением р0.

Сила давления жидкости на плоскую стенку равна произведению гидростатического давления в центре тяжести площади стенки рc на площадь стенки S:

Р= рc S [H].

Закон Паскаля гласит, что давление передается без изменения в каждую точку жидкой среды:

5

p1 = p2 ,

F1 = F2 ,

S1 S2

где F1 и F2 – силы, действующие на площадки S1 и S2.

Горизонтальная составляющая силы давления на криволинейную стенку равна силе давления жидкости на вертикальную проекцию стенки:

PГ = hc pgSпр ,

где hc – глубина, на которой расположен центр тяжести проекции стенки.

Относительный покой жидкости – это ее равновесие в движущихся сосудах, когда помимо силы тяжести действует сила инерции. Уравнение поверхности уровня имеет вид:

z = z0 + ω2r2 ,

2

где z0 – вертикальная координата вершины параболоида поверхности уровня, r, z – координаты любой точки поверхности уровня; ω – угловая скорость вращения.

Закон Архимеда гласит, что на тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости в объеме этого тела:

PA = ρж gVт .

где ρж – удельный вес жидкости; Vт – объем тела.

1.3. Основы кинематики и динамики жидкости

Уравнение Бернулли является основным уравнением гидравлики, определяющим связь между давлениями и скоростью в движущемся потоке жидкости.

Уравнение Бернулли в форме напоров имеет вид:

Пито и пьезометрической трубки), α1 и α2 – коэффициенты кинетической энергии (коэффициенты Кориолиса), hw - потери напора на гидравлические сопротивления между заданными сечениями.

Уравнение Бернулли можно записать в виде:

H1 = H 2 + hw ,

где H1 и H2 – полные напоры в сечениях 1 и 2.

Уравнение Бернулли в форме давлений имеет вид:

где ρghw – потери давления на преодоление сил трения и местные сопротивления.

Уравнение Бернулли в форме удельной энергии записывается в виде:

6

В этих уравнениях α1 и α2 – коэффициенты Кориолиса. Они определяются отношением действительной энергии потока к энергии, подсчитанной по средней скорости. Коэффициент α зависит от формы эпюры скорости:

α=2 – при ламинарном режиме течения;

α=1,1 – при турбулентном режиме.

Среднюю скорость потока жидкости можно выразить через расход:

υср = QS мс ,

где S – площадь живого сечения.

Расходы по длине трубы равны: Q1 = Q2 = … Qn .

1.4.Гидравлические сопротивления

1.Потери напора по длине

Потери напора hw складываются из потерь на трение по длине hдл и на местные сопротивленияhм :

hw = hдл + hм .

Потери напора на трение по длине определяются по формуле Дарси-Вейсбаха:

l υ2

hдл = λ d 2срg ,

где l – длина участка трубы диаметром d.

Безразмерный коэффициент сопротивления трения λ определяется в зависимости от режима течения. Определить, какой режим движения в трубе: ламинарный или турбулентный, можно по числу Рейнольдса:

Re = υνd ,

где ν– кинематическая вязкость.

При Re < 2320 – режим движения ламинарный, без перемешивания частиц жидкости и без пульсаций скоростей и давлений; при Re > 2320 – режим движения турбулентный, т.е. с перемешиванием жидкости и с пульсациями скоростей и давлений.

При ламинарном режиме коэффициент λ определяется по формуле:

λ = Re64 .

При турбулентном режиме коэффициент λ может зависеть как от числа Re так и от коэффициента эквивалентной шероховатости kэ трубы, который определяется экспериментально иприводитсяв справочниках.

Выбор функции для определения λ при турбулентном режиме зависит от области сопротивления, которую можноопределитьпосоотношению d/kэ ичислу Re:

при Re < 50 d/ kэ – область гидравлически гладких труб; при 50 d/kэ < Re < 500 d/ kэ – переходнаяобласть;

при Re > 500 d/kэ – областьгидравлическишероховатыхтруб.

Для области гидравлически гладких труб λ подсчитывается по формуле:

7

λ = 0,3164

Re0,25 .

Для переходной области:

Для области шероховатых труб:

λ = 0,11 kэ 0,25 .d

2. Потери напора на местных сопротивлениях

Местные потери напора происходят в так называемых гидравлических сопротивлениях, т.е. в местах изменения формы и размеров русла, где поток деформируется. МестныепотериопределяютпоформулеВейсбаха:

где ξм – коэффициент местного сопротивления.

Численное значение коэффициента ξм, в основном, определяется видом сопротивления и приводится в справочниках, но при небольшихчислахРейнольдса (ламинарное течение) зависит также иот Re. В этом случае потери напора на местных сопротивлениях определяются по формуле:

где lэ – эквивалентная длина, приводится в справочниках, зависит от диаметра трубопровода и вида сопротивления.

3. Истечение жидкостей из отверстий и насадков

При истечении жидкости из какого-либо резервуара происходит процесс превращения запаса потенциальной энергии вкинетическую энергию струи

Основной вопрос при решении практических задач - определение расхода вытекающей жидкостиивремениопорожнениярезервуарадляразличныхформотверстийинасадков. Отверстием называетсякруглоеотверстиеврезервуаре, диаметр котороговчетыре раза больше толщины стенки резервуара. Насадкомназываетсякороткаятруба, черезкоторую происходит истечение. Длина насадканедолжнапревышать4 егодиаметра. Вэтом случаеможнопренебречьпотеряминапораподлине.

Расход жидкости при истечении определяетсяпоформуле:

Q = μS0 2gH

где μ – коэффициент расхода, S0 – площадь отверстия или насадка, Н – расчетный напор: Расчетный напор можно определить по формуле:

H = H0 + (p0 − p),

ρg

где H0 – глубина жидкости, р0 – давление на свободной поверхности жидкости в резервуаре, р – давление на выходе из отверстия или насадка.

Если истечение происходит в резервуар, наполненный жидкостью, то в этом случае:

H0 = z1 − z2 ,

где z1 – глубина жидкости в первом резервуаре; z2 – глубина во втором.

8

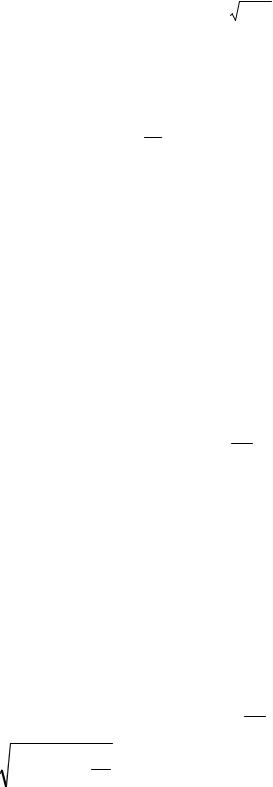
Иногда необходимоопределитьскорость вытекающейструина выходе из отверстия или насадка, в этом случае используется формула:

υ = ϕ 2gH ,

где ϕ – коэффициент скорости.

Значения коэффициентов ϕ и μ приводятся в справочниках в зависимости от вида отверстия или насадка:

μ = ϕ ε ,

где ε – коэффициент сжатия ε = Sc ,

S0

где Sc – площадь струи в сжатом сечении; S0 – площадь отверстия.

Значения коэффициентов истечения зависят отчисла Re, нодлябольших чисел Re (турбулентный режим) это изменение незначительно.

При истечении через насадок, при глубине жидкости в резервуаре > 14 м происходит срыв вакуума инасадок начинаетработать как отверстие в тонкой стенке.

1.5. Движение жидкостей в магистральных трубопроводах

При гидравлическом расчете длинных (магистральных) трубопроводов потери напора на преодоление местных сопротивлений составляют обычно не более 5% потерь напора на трение по длине и ими обычно пренебрегают. Движение воды в большинстве случаев относится к квадратичной зоне сопротивлений. Потери напора по длине определяются через модуль расхода К, зависящий от шероховатости и диаметра трубы и приводится в справочниках:

hдл = KQ2 2 l .

Для того, чтобы определить потребный напор Нтр, который необходимо создать в начале трубопровода используютформулу:

где z – перепад высот; pк – давление в конце трубопровода.

Если на участке простого длинного трубопровода производится непрерывная раздача жидкости по пути, то потери напора рассчитываются по формулам:

hдл = KQ2 2 l

Q2

где Qрасч = Qт2 + QpQт + 3p ; Qт – транзитный расход, Qp – распределяемый расход.

Последовательное соединение трубопроводов представляет собой несколько труб различной длины и диаметра, соединенных последовательно стык в стык. В этом случае потеря напора всего трубопровода равна сумме потерь в каждой трубе:

Расход в каждом сечении такого трубопровода постоянен:

9

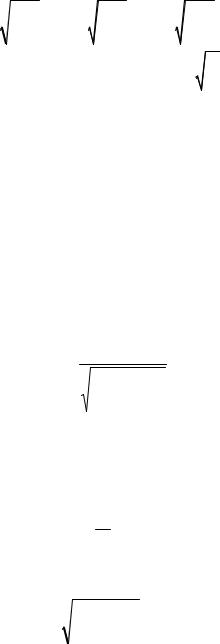
Q = Q1 = Q2 = ... = Qn .

Параллельное соединение трубопроводов представляет собой систему параллельно соединенных труб разной длины и диаметров, имеющих общий вход и выход. Общий расход системы в этом случае равняется сумме отдельных расходов. Для определения расходов в ветвях составляются уравнения:

Для каждой ветви составляется система, один из расходов выражается через общий расход:

Qn = Q − Q1 − Q2 − ...

Гидравлическим ударом называется резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении жидкости, вызванном быстрым закрытием крана. В этом случае давление в трубопроводе может быть в несколько раз выше расчетного, итрубопровод можетбытьразрушен.

Давление при гидравлическомударе определяется поформуле:

где ρ – плотность жидкости; υ0 – скорость; Еж – модуль упругости жидкости; Етр – модуль упругости трубы; r – радиус трубы; δ – толщина стенки трубы.

Этаформуласправедливаприпрямомударе, когдавремязакрытиякранаменьше фазы гидравлического удара:

t0 = 2cl ,

где с– скоростьраспространенияударнойволны:

При непрямом гидравлическом ударе, когда время закрытия крана больше фазы гидравлического удара, повышение давления в трубопроводе можноприблизительно определитьпоформуле:

1.6. Основы моделирования

Расчет моделей ведется с учетом соблюдения критериев подобия:

10