4. Построение переходных процессов. Методы

Для построения переходных процессов используются методы: 1) метод непосредственного решения (классический метод); 2) использование преобразований Фурье, Лапласа, Карсена-Хевисайда; 3) метод трапецидальных частотных характеристик, 4) сведение неоднородного уравнения к однородному; 5) численный графический метод Башкирова; 6) использование ЭВМ.

ДУ через полиномы

Гдеf– возмущение, g- управляющее воздействие.

Свободная составляющая получается путем решения однородного уравнения

Частное решение определяется правой частью уравнения, т.е.

Частному решению будет соответствовать некоторый устан-ся режим в системе существующий после затухания.

а₀рⁿ+ а₁р^n-1 + а₂р^n-2 +...+ а _n – линейное д/у

Метод сведение неоднородного уравнения к однородному.

Преоб-ие Карсена-Хевисайда

p*W(p)

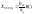
Введем новую переменную

Z(t)=X(t)-Xуст=X(t)-b_m/a_n*1=

Этому решению соот-ет исходное д/у без правой части:

Новое ур-ие.

Найдем начальные усл-ия для новой переменной

Начальные усл-ия до и после нанесения возмущения:

Z=X(t) – X(∞)

X(t)=Z(t) + X(∞)

Метод трапецидальных частотных характеристик.

ᵆ=ω_d/ω₀ – коэф-т наклона трапеции

На основании интегралов Фурье

Оригинал искомой величины будет пред-ся след-м виде:

x(t) =

Порядок построения П/П методом трапецидальных хар-к:

1. Находим обобщенную вещественно-частотную характеристику замкнутой системы. 2.строим график ВЧХ в зависимости от частоты. 3.разбиваем ВЧХ на прямоугольные треугольники и трапеции, у которых одна из сторон является частью мнимой оси. 4.фиксируем параметры (высота, W0, Wd, χ). 5.Строим кривые функции времени для каждого Δ и трапеции. ;- переход к реальным значениям.H –высота Δ и трапеций. h-значение из приложения.где ω – полоса пропускания частот.

Численно-графический метод Башкирова.

а – начало единичного воздействия

Метод Башкирова разработан для кривой переходного процесса звена I порядка. 1) Выбирается масштаб по координатам x_вых и t. 2) По ординате откладывается величина kx_вх. Через полученную точку проводится вспомогательная прямая параллельная оси абсцисс. 3) На вспомогательной прямой откладываются интервалы времени Δt намного меньше, чем Т Δt<< Т. И на ней отмечается т. а на расстоянии Т + Δt/2 от начала координат. 4) Из начальной координаты в т.А проводят прямую; с конца отрезка первого отрезка Δt восстанавливают перпендикуляр до пересечения с этой прямой. Получают первую точку кривой переходного процесса. Со 2-ой точки в проводим прямую, в т 1, с конца 2-го отрезка Δt восстановим перпендикуляр до пересечения с линией 1в, получим 2-ую т. П/П и т.д.