6. Идеальный операционный усилитель

Идеальный ОУ имеет коэффициент усиления по напряжению: K_U=U_BbIX/U_BX; K_U→ ∞; R_BX→ ∞; R_BbIX→ 0. ОУ является усилителем пост. тока. В ОУ очень мал дрейф нуля. Вых. напряжение для дифференциального ОУ: U_BbIX= K_U(U_{BX 1}- U_{BX 2}). При подаче сигнала на прямой вход: U_BbIX= K_U(U_{BX 1}), а при подаче на инвертирующий: U_BbIX= -K_UU_BX.

Для улучшения параметров УО применяют ОС.

Будем называть идеальным операционный усилитель, который имеет следующие свойства:

-бесконечно большой дифференциальный коэффициент усиления по напряжению K_U=U_вых /(U₁ – U₂) (у реальных ОУ от 1 тыс. до 100 млн.);

-нулевое напряжение смещения нуля U_см,;

-нулевые входные токи;

-нулевое выходное сопротивление (у реальных маломощных ОУ от десятков Ом до единиц кОм);

-коэффициент усиления синфазного сигнала равен нулю;

-мгновенный отклик на изменение входных сигналов.

Как будет показано ниже, операционный усилитель, предназначенный для универсального применения, из соображений устойчивости должен иметь такую же частотную характеристику, что и фильтр нижних частот первого порядка, причем это требование должно удовлетворяться, по крайней мере, вплоть до частоты единичного усиления f_Т, (т.е. частота, при которой |K_U|=1). На рис. 20 представлена типичная логарифмическая амплитудно-частотная характеристика (ЛАЧХ) скомпенсированного операционного усилителя. В комплексной форме дифференциальный коэффициент усиления такого усилителя выражается формулой:

(14)

где K_U – дифференциальный коэффициент усиления ОУ на постоянном токе.

Рис. 1 Логарифмическая АЧХ операционного усилителя

Выше частоты f_п, соответствующей границе полосы пропускания на уровне 3 дБ, модуль коэффициента усиления K_U обратно пропорционален частоте. На частоте f_Т модуль дифференциального коэффициента усиления |K_U|=1. Как следует из последнего выражения, частота f_Т равна произведению коэффициента усиления на ширину полосы пропускания.

7. Дифференциальные схемы с оу

Дифференциальное включение

На рис. 21 приведена схема дифференциального включения ОУ. Найдем зависимость выходного напряжения ОУ от входных напряжений. Вследствие свойства идеального операционного усилителя (K_U) разность потенциалов между его входами p и n равна нулю. Соотношение между входным напряжением U₁ и напряжением U_p между неинвертирующим входом и общей шиной определяется коэффициентом деления делителя на резисторах R₃ и R₄:

(15)

Поскольку напряжение между инвертирующим входом и общей шиной U_n=U_p, ток I₁ определится соотношением:

(16)

Вследствие свойства идеального ОУ I₁=I₂. Выходное напряжение усилителя равно:

(17)

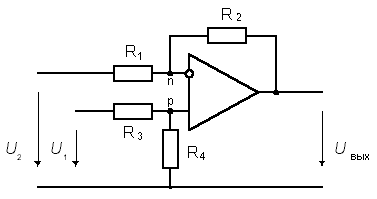
Рис. 2 Дифференциальное включение ОУ

Подставив (15) и (16) в (17), получим:

(18)

При выполнении соотношения R₁R₄ = R₂R₃,

8.Алгебра логики. Основные понятия и тождества.

Логические сообщения – это сообщения истинность и ложность которых может быть оценена однозначно. Каждое логическое сообщение может быть заменено математическим эквивалентом, т.е. логической функцией. Логические функции в отличие от аналоговых принимают лишь два значения 0 и 1. логические операции:

1) «НЕ» – логические отрицание или инверсия;

2) «ИЛИ» – сложение или дизъюнкция (). Операцию «ИЛИ» можно выполнять для 2^х, 3^х и более переменных. Выходная функция равна 1, если хотя бы одна из независимых входных переменных равна 1.

3) «И» – логическое умножение или конъюнкция.().

4) Сложение (сумма) по модулю 2 (Исключающее_ИЛИ)(+)«1» если входы равны.

5) стрелка пирса (или-не)(↓)

6) штрих шеффера ( и-не)(∕)

Справедливы законы:

1)переместительный a+b=b+a; a*b=b*a

2) сочетательный а+(в+с)=(а+в)+с; а*(в*с)=(а*в)*с

3)распределительный а*(в+с)=а*в+а*с; а+(в*с)=(а+в)*(а+с)

4)Закон поглощения: а(а+в)=а; а+ав=а; а(а+в)(а+с)=а; а+ав+ас=а.

5)Закон склеивания: ;

Для осуществления операций над логическими выражениями пользуются рядом тождеств:

1) А+А=А; 2) ; 3) А+0=А; 4) А+1=1; 5) АА=А; 6) ; 7) А0=0; 8) А1=А; 9) ; 11); 12); 13).

Используя данные тождества можно упростить логические уравнения и свести к минимуму число логических элементов необходимых для реализации логич функции. Следующие тождества называются формулами де Моргана:

,

Совокупность элементарных функций с помощью которых можно записать логическую функцию более сложного вида называется базисом.

Синтез логич схем в базисе И-НЕ

Синтез логич схем в базисе ИЛИ-НЕ

.

9. Минимизация логических функций. Общие сведения. Диаграммы вейча

Упрощение логических функций с помощью тождеств (аналитический) основывается на интуитивных решениях, и представляет трудности особенно при большем числе вх переменных. При этом трудно оценить, является ли полученное выражение минимальным или возможно дальнейшее упрощение. В этом случае приминяются методы минимизации:

1)диагр Вейча,

2)Карты карно - предусматривает задание ФАЛ в виде координатных карт состояний. После записи ФАЛ в карту Карно сразу можно записать минимальную форму функции, что существенно уменьшает вероятность появления ошибки, метод Квайна-Мак-Класки использование метода для функций с большим количеством аргументов и значительно уменьшает вероятность появления ошибки,

3)мет.неопред.коэфф

4)метод непосредственных преобразований логических функций- базируется на преобразовании ФАЛ с использованием основных законов и тождеств АЛ

Метод диаграмм Вейча (карта Карно).

Данный метод используется в основном для 2^х, 3^х, 4^х 5^ти переменных. 1.Задается некоторое логическое уравнение, которое необходимо преобразовать(исключить общие знаки инверсии, применить закон де Моргана, повторения, поглощения и склеивания) Привести к виду СДНФ, СКНФ

2.Заполнить диаграмму Вейча, если в данном выражении есть соответствующие комбинации вх переменных, то клетки диаграммы обозначаются единицей

3.Проводится склейка клеток, т.е. можно объединить целую заполненную строку, целый столбец, полстроки, полстолбца. Можно склеивать соседние строки, столбцы, полустроки, полустолбцы. Можно объединять нижний, верхний, правый и левый края. Нельзя соединить нечетн число клеток клетки по диагонали.

4.Расшифровка склеек. Каждая склейка в результате должна быть представлена в виде конъюнкции переменных. В результате расшифровок склеек получаем результат минимизации, т.е. новое упрощенное логическое выражение.

5. строится новая логическая схема, в выбранном базисе.

Метод минимизации функций с помощью диаграммы Вейча очень прост и использование данного метода заменяет массу сложнейших преобразований с помощью разнообразных тождеств.

Пример: М-д диаграммы Вейча

Предположим что задана логич. фун-я:

f=х₁х₂х₃ v х₁/х₂х₃ v /х₁/х₂/х₃ v /х₁/х₂/х₃ v х₁х₂/х₃.

2 ЭТ.- заполнение клеток диагр. Вейча:

f = х₁х₂ v /х₁/х₂ v х₁х₃.