1. Разомкнутые и замкнутые сар. Передаточные функции и частотные характеристики. Методы.

САР - система, состоящая из объекта управления и регулятора, в котором автоматически выполняется заданный процесс.

Разомкнутые САР - системы, в которых входными воздействиями управляющего устройства являются только внешние (задающие и возмущающие) воздействия; при этом значение выходной величины ОУ может существенно отклоняться от его заданного значения в силу изменения внутренних свойств ОУ, параметров САР. Разомк-ые САР состоит из 2 звеньев объекта и регул-ра. Объект воздей-ет на регу-ор. Если разомк-ую цепь замкнуть, то получим замкнутую САР.

Для автоматического поддержания выходной величины на заданном уровне используют замкнутые САР с обратной связью.

W_З­=W_P / (1+W_P) перед ф зам. сар.

Связь м/у передат-ми ф-ми замк-ой и разом-ой САР:

W_з=W_р(р)/(1+W_р(р)W_ос(р))

Пусть САР описывается линейным дифференциальным уравнением вида

d/dt=p

Перед-ая ф-я W(p) – отнош-ие изобра-ия вых. вели-ы к изобра-ию вх. вел-ны.

Сделаем замену p→jω(Фурье)

- прямое преобр-ие Фурье

- обратное преоб-ие Фурье

Преоб-ие Лапласа связано с понятием о перед-ой функции.

Преоб-ие Фурье связано с понятием о част-х харак-х.

p→jωПолучим АФХW(jω)=R(ω)+jJ(ω),

АЧХ – зависи-ть отнош-ия амплитуд вых. и вх. сигнала от частоты.АЧХ (модуль) .

ФЧХ – зависи-ть фазового сдвига м/у вх. и вых. сигн-ми от частоты.

φ(ω)=arсtg(J(ω)/R(ω)).

Величину R(ω) называют вещественной частотной характеристикой (ВЧХ),J(ω) - мнимой частотной характеристикой.

2. Критерии устойчивости сар.

Устойчивость САР - свойство системы возвращаться в исходное состояние равновесия после прекращения воздействия, выведшего систему из этого состояния.

Правила, с помощью которых можно судить о знаках корней, не решая характ-ое урав-ие, наз-ют крите-ми устойч-ти.

Крит-ии устой-ти: алгебра-ие (устанавливают необходимые и достаточные условия отрицательности корней в форме ограничений, накладываемых на определенные комбинации коэффициентов характ. уравнения) и частотные (определяют связь между устойчивостью системы и формой частотных характеристик системы).

Алгебр-ие критерии

Теорема Ляпунова: для устойчивости САР необходимо и достаточно, чтобы все корни характеристического уравнения располагались бы слева от мнимой полуоси. Если хотя бы один корень будет находится справа, то сис-ма будет неустойчивой. Простейший критерий устойчивости - условие положительности коэффициентов характеристического уравнения (необходимое условие).

Критерий Раусса - Гурвица.

САР описывается характ. ур-ием:

а₀рⁿ + а₁р^n-1 + а₂р^n-2 +...+ а_n =0.

Первый коэф-т при старш. Произ-ой д.б. больше 0.

САР устойчива, если при а₀>0 положительны все определители Δ₁, Δ₂, …, Δ_nвида

Если хотя бы один из определителей = 0 - система на границе устойчивости. Т.е. нужно чтобы все коэффициенты характеристического уравнения и определитель Δ _n-1были положительными.

Если хотя бы один из определителей Гурвица отриц-ый, то сис-ма неустойчива.

Критерий устойчивости Вышнеградского.

САР описывается характ. ур-ием: а₀р³ + а₁р² + а₂р + а₃ =0. Разделим обе части уравнения на а₀. Получим

р³ + а₁ / а₀р² + а₂ / а₀р + а₃ / а₀=0. Примем, что

а₁ / а₀ =С₁, а₂ / а₀=С₂, а₃ / а₀=С₃. Тогда р³ + С₁р² + С₂р + С₃ =0.

Х и У – параметры Вышнеградского

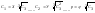
Тогда ψ ³+А ψ²+В ψ +1=0.

Исп-ем критерий Гурвица.

-условие устойчивости. Если АВ=1, то система находится на границе устойчивости. АВ<1 не устойчив

I– обл-ть не устой-ти,II– обл-ть устой-ти,III– перех-ой процесс сходящ-ся,IV– перех-ой процесс апериодически сходя-йся,V- перех-ой процесс колебательно-сходящийся. В т.С сис-ма будет идеальной.

Для того, чтобы выбрать структурную схему желательно устойчивой, необ-мо по диаграмме Вышнеградского выбрать соот-ий переходной процесс. По этим параметрам опр-ют коэф-ты хар-го ур-ия.1