1. 2.Модели множественной регрессии. Корреляционный анализ. Оценка тесноты линейной и нелинейной связи.

Наиболее простыми моделями множественной регрессии являются модели вида: . Величины распределены по нормальному закону. Введем след. Обозначение вектор столбец значений зависимой переменной..Матрица значений переменных :Матрица коэффициентов уравнения:

Y=XA матричная форма. Применение МКТ предполагает решение оптимизационной задачи:

В матричном виде: .. Т.к, то оно совпадает со своим транспонированным значением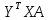.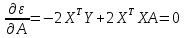, т.е. Решая данное уравнение относительно А получим матричную форму для оценки параметров:

Для оценки тесноты лин связи определяют выборочный коэф-т корреляции:

показывает что м/у коэф-тами лин ур-я сущ-ет корреляц-ая зав-ть, где

Для оценки тесноты нелин связи – кор-ое отношение:

чем больше θ, тем сильнее связь.0<=θ<=1.Если =1,то сущ-ет функциональная зав-ть, при =0 связь м/у Y и X может появиться в ур-ях более высокого порядка.

Используют если необходимо исследовать корр-ю связь м/у многими величинами.

Исходный материал заносят в таблицу:

i	X1	X2	. . .	Xk	Y
1	X11	X12	. . .	X1k	Y1
2	X21	X22	. . .	X2k	Y2
. . .	. . .	. . .	. . .	. . .	. . .
n	Xn1	Xn2	. . .	Xnk	Yn

Переходят к новому масштабу:

Материал вновь заносят в табл.

В новом масштабе

Выборочный коэф-т корреляции в этом случае:

Ур-е регр-ии примет вид:

Коэф-ты находятся из усл-ия:

Найдем частные производные ур-я регрессии, сост-м сист-у:Умножим на 1/(N-1).

Получаем систему ур-ий:

коэф-ты корр-ии вычисляются перемножением соотв-х столбцов табл с новыми переменными.

Решив систему расчитываем коэф-т мн-ой корреляции:

Служит показателем силы связи, от 0 до 1.

Для практического использования ур-ия перейдем к натур. масштабу:

6. Классификация объектов управления. Регулирование давления. Уравнения динамики.

Классификация:

По характеру протекания технологического процесса (Циклические, Непрерывно-циклические,Непрерывные)

По характеру установившегося значения выходной величины объекта (Объекты с самовыравниванием-после нарушения равновесия возвращается к нужному состоянию самостоятельно, без участия человека, Объекты без самовыравнивания)

По структуре объекта (Без запаздывания, С запаздыванием)

По количеству входных и выходных величин и их взаимосвязи (Одномерные-один вход и один выход, Многомерные многосвязные – когда наблюдается взаимное влияние технологических параметров друг на друга, Многомерные несвязные - взаимосвязь между каналами которых мала)

По виду статических характеристик и характеру математических соотношений (линейные, нелинейные)

По распределенности объекта управления (локальные, распределенные ОУ)

По типу стационарности (стационарные, нестационарные – параметры объекта с течением времени изменяются, н-р, самолет, масса которого меняется)

По направлению действия (Прямого и обратного действия)

Объект регулирования- ёмкость с газом.

Поведение идеальных газов описывается ур-ем Менделеева-Клапейрона. pV=MRT, (*)

где p-давление,V-объем,M-число молей газа,R-универсальная газовая постоянная 8,31Дж/К моль.Т-абс.темп-ра.

М=m/μ- количество молей газа

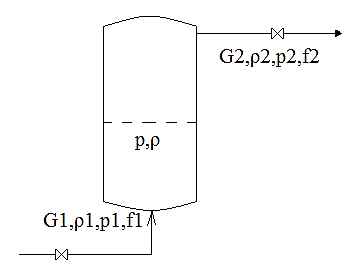
ρ₂=ρ₁,ρ – плотность газа

1-вх параметр

2-вых праметр

G₁,G₂- массовый расход

F₁,F₂- проходное сечение

p₁,p₂, p – избыточное давление на вх., вых. и внутри (p₂ =p_атм)

Ур-е статики емкости: G₁=G₂ (1)

Ур-е динамики: или(1б)

из уравнения (*) выражаем m=(pVμ)/RT

Примем V,T=const, тогда через приращение

(2)

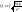- обьемный расход газа

где с- постоянная расхода, Δр-перепад давления,Q-объемный расход.

G=Q*ρ;

(3)

Из условия, что ρ₂₌ρ, из (*) выразим

Подставляя в выражение (3) и линеаризуя получим G₂

(4)

Подставив (2) и (4) в выражение (1б) получим:

Приведем к виду:

Разделим наполучим: