3.Планирование экспериментов. Полный факторный эксперимент.

Рассмотрим оптимальный двухуровневый план 2^к, где к-число параметров. При планировании экспериментов условия опытов представляют собой фиксированное число значений, уровней для каждого фактора. Если эксперименты проводят на двух уровнях при двух значениях факторов, то постановку опытов наз-ют полный факторный эксперимент. Уровни факторов представляют собой границы исследуемой области по технологическому параметру.

Шаг вариирования:

Центр плана:

Переход к безразмерным единицам:

Необходимо получить полное уравнение регрессии с коэф-тами взаимодействия:

Пример.

Z₁ изментяется от 100 до 200 ед. изм.

Z₂ измен-ся от 20 до 60 ед. изм.

Z₃ измен-ся ри 10 до 30 ед.изм.

;;;

;;;

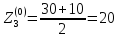Запишем план проведения экспериментов в виде матрицы планирования:

Матрица планирования 2³

Матрица планирования с фиктивной переменной:

Рассчитаем линейные коэф-ты регрессии:

;;;;

;;;;

Итоговое уравнение регрессии:

;

4.Экспериментальные методы получения динамических характеристик. Корреляционный метод идентификации. Уравнение Винера-Хопфа.

Динамическим характеристикам объектаотносятся: 1.Переходная функция. 2.Весовая функция. 3.Дифференциальные уравнение. 4.Передаточная функция. 5.Все частотные характеристики.

Все эти характеристики связаны между собой преобразованиями Лапласа и Фурье. Имея одну из этих характеристик можно получить остальные.

Прямое преобразование Лапласа Обратное преобразование Лапласа

Экспериментальный метод нахождения динам. хар-кактивным способом закл. в опред-нии хар-ра реакции объекта на тот или иной вид возмущ. возд-вия (импульс, единичное, синусоида)

Найдем уравнение объекта по его временной хар-ке:

Рассмотрим уравнение 1-го пордка для простых объектов

-диф. ур-ние 1-го порядка

По найденным значениям К и Т строим зависимость по решению диф. уравнения 1-го порядка. Расхождение м/у кривыми д. составлять 3-5%. Если расхождение значи-ые, след-но, нужно пересчитать пар-р Т. На точность Т м. влиять правильность проведения касат. к кривой в нач. точке.

Д/объекта 2го порядка м. записать след. уравнение:

Решение этого уравнения имеет следующий вид:

_{Корреляционный метод индентификации}

Вых. перемен. объекта y(t) опр-ся не т/о детерминированными ур-ми входн. сигналовu(t), но и наблюдаемыми и неуправляемыми возд-ми (помехами)

Д/колисественной оценки и сравнения разл. случ. сигналов исп. разл. хар-ки этих сигналов: 1) ф-ция распрю. вер-тей случ. проц; 2) плотность вер-тей; 3) мат. ожидан. случ. проц.; 4) дисперсия слу. проц.; 5) корреляц. ф-ция; 6) спектральная плостность.

Коррел. ф-ция: 1) автокорреляционная (R_xx) – это мат. ожидание произведений 2х знач. одного и того же сигнала сдвинутых по времени. 2) взаимная корр. ф-ция – мат. ожидание произведений 2х сигналов 1 их к-х сдвинут относ-но др по времени.

Оценка кор. ф-ции: ,-центрированные случайный сигнал (процесс с нулевым средним значением)

Спектральная плотность – это ф-ция, к-я пок-ет распр-ие мощности сигнала по частотам.

;

;

–уравнение Виннера-Хопфа. Это ур-ие относ-ся к лин-му интегрир. ур-ию 1-го рода. Его численное реш-ние осущ методами апроксимирующих ф-ций, к-е выч-ся на основе методов холлокации Галеркина в конечных элементах, наим. квадратов. Результат решения этого уравнения – ф-ция веса обекта.