
Базы / Оптимизация диф.зачет.испр
.doc|
1 |
1 |
В чем заключается оптимизация любого процесса? |
в нахождении оптимума рассматриваемой функции или соответственно оптимальных условий проведения данного процесса |
в выборе критерия оптимизации |
в улучшении двух или более количественных характеристик |
в нахождении экстремума целевой функции |
|
1 |
|
2 |
1 |
В чем заключается задача оптимизации? |
в нахождении оптимума рассматриваемой функции или соответственно оптимальных условий проведения данного процесса |
в выборе критерия оптимизации |
в улучшении двух или более количественных характеристик |
в нахождении экстремума целевой функции |
|
4 |
|
3 |
1 |
Что называется целевой функцией? |
критерии оптимизации |
зависимость критерия оптимизации от параметров, влияющих на его значение |
зависимость выхода продукта от температуры и давления |
создание и реализация оптимальной модели процесса |
создание и реализация системы оптимального управления процессом |
2 |
|
4 |
1 |
Статическая оптимизация – это… |
критерии оптимизации |
зависимость критерия оптимизации от параметров, влияющих на его значение |
зависимость выхода продукта от температуры и давления |
создание и реализация оптимальной модели процесса |
создание и реализация системы оптимального управления процессом |
4 |
|
5 |
1 |
Динамическая оптимизация – это… |
критерии оптимизации |
зависимость критерия оптимизации от параметров, влияющих на его значение |
зависимость выхода продукта от температуры и давления |
создание и реализация оптимальной модели процесса |
создание и реализация системы оптимального управления процессом |
5 |
|
6 |
1 |
Аналитический поиск экстремума целевой непрерывной функции сводится к следующему уравнению: |
|
|
|
|
|
3 |
|
7 |
1 |
Вспомогательная функция метода Лагранжа имеет вид: |
|
|
|
|
|
2 |
|
8 |
1 |
Из каких уравнений находятся экстремальные точки функции F(x1,…xn) по методу Лагранжа? |
|
|
|
|
|
14 |
|
9 |
1 |
Какие условия должны выполняться при решении задачи минимизации по методу геометрического программирования? |
|
|
|
|
ai1x1+ ai2x2+…+aimxm≥ bi |
24 |
|
10 |
1 |
Для минимизации каких алгебраических выражений применяется метод геометрического программирования? |
|
|
|
|
ai1x1+ ai2x2+…+aimxm≥ bi |
1 |
|
11 |
1 |
Укажите теорему о среднем, на которой основан вид геометрического программирования? |
|
|
|
|
ai1x1+ ai2x2+…+aimxm≥ bi |
3 |
|
12 |
1 |
В каком виде задаются ограничения в методе линейного программирования? |
|
|
|
|
ai1x1+ ai2x2+…+aimxm≥ bi |
5 |
|
13 |
1 |
Метод геометрического программирования принимают для… алгебраических выражений |
алгоритмизации |
минимизации |
нахождение максимума |
нахождение экстремума |
|
2 |
|
14 |
1 |
Метод Лагранжа используется, когда на переменные накладываются ограничения в виде… |
неравенств |
равенств |
равенств и неравенств |
чисел |
|
2 |
|
15 |
1 |
Какой принцип используется в методе динамического программирования? |
экстремальности |
условности |
оптимальности |
реализации |
оптимизации |
3 |
|
16 |
1 |
Для каких процессов применяется метод динамического программирования? |
любых |
одностадийных |
многостадийных |
многофункциональных |
|
3 |
|
17 |
1 |
Основное уравнение метода динамического программирования имеет вид:… |
|
F=c1x1+c2x2+…+cnxn |
F(x)=3xA+5xB |
F=F(x1;x2;…xn) |
|
1 |
|
18 |
1 |
Целевая функция метода линейного программирования имеет вид: |
|
F=c1x1+c2x2+…+cnxn |
F(x)=3xA+5xB |
F=F(x1;x2;…xn) |
|
2 |
|
19 |
1 |
Как определяется градиент в точке (х1;х2;…хn) |
|
|
F=c1x1+c2x2+c3x3 |
|
|
4 |
|
20 |
1 |
Как вычислить размер шага в градиентных методах? |
|
|
F=c1x1+c2x2+c3x3 |
|
|
2 |
|
21 |
1 |
Чему равен косинус градиента в i-ом направлении? |
|
|
|
|
|
1 |
|
22 |
1 |
Градиент в точке (х1,х2…хn) определяется… |
точкой |
оптимальным значением |
переменной |
вектором |
размером шага |
4 |
|
23 |
1 |
В какой точке градиент строго ортогонален к поверхности? |
в начальной |
в конечной |
в центральной |
в базисной |
|
14 |
|
24 |
1 |
Переключение на метод градиента происходит когда система находится вблизи минимума, показателем чего является малое значение величины… |
|
|
|
|
|
4 |
|
25 |
1 |
Как найти значения рабочих шагов в методе наискорейшего спуска? |
|
|
|
|
|
35 |
|
26 |
1 |
Как найти инкремент? |
Ix = xопт – х0 |
|
|
|
|
12 |
|
27 |
1 |
Как найти xопт по методу двух производных? |
xопт = х0 - Ix |
xопт = х0 + Ix |
xопт
= -
|
|
|
23 |
|
28 |
1 |
Что представляет собой принцип максимума? |
Совокупность ряда терем теории оптимальных процессов |
Совокупность переменных величин в теории оптимальных процессов |
Управляющие воздействия |
Фазовую траекторию движения объекта |
Фазовое пространство |
1 |
|
29 |
1 |
Что называется фазовыми координатами? |
Совокупность ряда терем теории оптимальных процессов |
Совокупность переменных величин в теории оптимальных процессов |
Управляющие воздействия |
Фазовую траекторию движения объекта |
Фазовое пространство |
2 |
|
30 |
1 |
Какие существуют формы слепого поиска? |
Локальный поиск |
Поиск с анализом промежуточных результатов |
Сканирование |
Метод Гаусса-Зейделя |
Чисто случайный поиск |
35 |
|
31 |
1 |
В чем заключается метод слепого поиска? |
Программа поиска не установлена заранее, а зависит от результатов предшествующих наблюдений |
В просматривании точек допустимой области в заранее установленном порядке или без всякого порядка |
Точка перемещается по некоторой линии, причем пробные перемещения позволяют определить направление, в котором следует перемещаться, чтобы уменьшить значение функции |
Все ответы верные |
|
2 |
|
32 |
1 |
В чем заключается метод сканирования?: |
Программа поиска не установлена заранее, а зависит от результатов предшествующих наблюдений |
Точки области одна за другой просматриваются в определенном порядке |
Точка перемещается по некоторой линии, причем пробные перемещения позволяют определить направление, в котором следует перемещаться, чтобы уменьшить значение функции |
Точки на плоскости выбираются случайно с неизменным законом распределения |
|
2 |
|
33 |
1 |
В чем заключается чисто случайный поиск? |
Программа поиска не установлена заранее, а зависит от результатов предшествующих наблюдений |
Точки области одна за другой просматриваются в определенном порядке |
Точка перемещается по некоторой линии, причем пробные перемещения позволяют определить направление, в котором следует перемещаться, чтобы уменьшить значение функции |
Точки на плоскости выбираются случайно с неизменным законом распределения |
|
4 |
|
34 |
1 |
В чем заключается поиск с анализом промежуточных результатов? |
Программа поиска не установлена заранее, а зависит от результатов предшествующих наблюдений |
Точки области одна за другой просматриваются в определенном порядке |
Точка перемещается по некоторой линии, причем пробные перемещения позволяют определить направление, в котором следует перемещаться, чтобы уменьшить значение функции |
Точки на плоскости выбираются случайно с неизменным законом распределения |
|
1 |
|
35 |
1 |
В чем заключаются методы локального поиска? |
Программа поиска не установлена заранее, а зависит от результатов предшествующих наблюдений |
Точки области одна за другой просматриваются в определенном порядке |
Точка перемещается по некоторой линии, причем пробные перемещения позволяют определить направление, в котором следует перемещаться, чтобы уменьшить значение функции |
Точки на плоскости выбираются случайно с неизменным законом распределения |
|
3 |
|
36 |
1 |
В качестве классов функций сравнения используются следующие множества функций… |
С |
С1 |
ρ0 |
ρ1 |
Ј |
12 |
|
37 |
1 |
Расстоянием нулевого порядка называется число… |
С[хо;х1] |
С1[хо;х1] |
ρ0 |
|
Ј(y(x))= |
3 |
|
38 |
1 |
… связывает критерий оптимизации с переменными параметрами, влияющих на его значение |
Целевая функция |
Вариационная функция |
Критерий оптимизации |
Параметр оптимизации |
|
1 |
|
39 |
1 |
В линейном программировании ограничения задаются в виде … |
равенств |
неравенств |
смешанно |
Все ответы верные |
|
3 |
|
40 |
1 |
В методе Лагранжа число множителей Лагранжа определяется … |
числом ограничений |
числом входных параметров |
суммой числа ограничений и входных параметров
|
|
|
1 |
|
41 |
1 |
Основная цель оптимизации заключается |
В нахождении всех возможных решений |
В нахождении оптимального решения кратчайшим способом |
В нахождении оптимального решения |
Все ответы верные |
|
3 |
|
42 |
1 |
Стадии оптимизации? |
Классическая |
Статическая |
Динамическая |
Минимальная |
Максимальная |
23 |
|
43 |
1 |
Экстремум – это … целевой функции |
Критерий |
Максимум |
Метод |
Минимум |
|
24 |
|
44 |
1 |
Методы математического программирования? |
Аналитическое программирование |
Динамическое программирование |
Геометрическое программирование |
Статическое программирование |
Линейное программирование |
235 |
|
45 |
1 |
Сколько множителей Лагранжа вводится на одно ограничение? |
Два |
Три |
Один |
Четыре |
Пять |
3 |
|
46 |
1 |
Сколько множителей Лагранжа вводится на три ограничения? |
Два |
Три |
Один |
Четыре |
Пять |
2 |
|
47 |
1 |
На какой теореме основан метод геометрического программирования? |
Геометрической |
О среднем |
Математической |
Алгебраической |
|
2 |
|
48 |
1 |
С какой стадии начинается рассмотрение в методе динамического программирования? |
С первой |
Со второй |
С последней |
С центральной |
|
3 |
|
49 |
1 |
Метод динамического программирования предполагает разбиение анализируемого процесса на … |
Переменные |
Стадии |
Уравнения |
Ступени |
Шаги |
24 |
|
50 |
1 |
Метод …производных? |
Трех |
Двух |
Четырех |
|
|
2 |
|
51 |
1 |
Для определения составляющих градиента делаются … шаги |
Большие |
Рабочие |
Минимальные |
Пробные |
Дополнительные |
4 |
|
52 |
1 |
По какому направлению делаются рабочие шаги по отношению к градиенту? |
Противоположному |
Прямому |
Перпендикулярному |
Параллельному |
|
1 |
|
53 |
1 |
Сколько рабочих шагов делается в методе градиента после определения градиента? |
Два |
Множество |
Один |
Несколько |
|
3 |
|
54 |
1 |
Какой принцип
описывается системой дифференциальных
уравнений
|
Оптимальности |
Максимума |
Минимума |
Аналитический |
Классический |
2 |
|
55 |
1 |
Как называется совокупность переменных величин в теории оптимальных процессов? |
Фазовыми координатами |
Управляющими воздействиями |
Экстремальные точки |
Факторами |
|
1 |
|
56 |
1 |
Как называется управляющее устройство в системе автоматической оптимизации? |
Вычислительное устройство |
Устройство вычисления критериев |
Оптимизатор |
Канал |
|
3 |
|
57 |
1 |
Как называют цепи переменных в процессе автоматической оптимизации? |
Вычислительное устройство |
Устройство вычисления критериев |
Оптимизатор |
Каналы |
|
4 |
|
58 |
1 |
Как называется n-мерное пространство в принципе максимума? |
Управляющее |
Оптимальное |
Экстремальное |
Фазовое |
|
4 |
|
59 |
1 |
Как найти вариацию функционала? |
|
Ј(y(x))= |
|
ρ0 |
|
3 |
|
60 |
1 |
Как найти расстояние 1-го порядка? |
|
|
|
Ј(y(x))= |
ρ0 |
2 |
|
61 |
2 |
Какие применяют методы в случаях, когда информации о процессе недостаточно? |
экспериментальные |
статические |
эксперементально-статистические |
эксперементально-статические |
статистические |
3 |
|
62 |
2 |
Какой бывает эксперимент? |
массивный |
активный |
пассивный |
неактивный |
|
23 |
|
63 |
2 |
В каком эксперименте ставится большая серия опытов с поочередным варьированием каждой из переменных? |
массивный |
активный |
пассивный |
неактивный |
реактивный |
3 |
|
64 |
2 |
Какой эксперимент ставится по заранее составленному плану с одновременным изменением всех параметров? |
массивный |
активный |
пассивный |
неактивный |
реактивный |
2 |
|
65 |
2 |
Что называется факторами? |
поверхность отклика |
пространство с координатами х1,х2,…хn |
независимые переменные х1,х2,…хn |
функция отклика |
параметр оптимизации |
3 |
|
66 |
2 |
Что является математической моделью в пассивном эксперименте? |
поверхность отклика |
пространство с координатами х1,х2,…хn |
независимые переменные х1,х2,…хn |
функция отклика |
параметр оптимизации |
4 |
|
67 |
2 |
Как называется геометрическое изображение функции отклика? |
поверхность отклика |
пространство с координатами х1,х2,…хn |
независимые переменные х1,х2,…хn |
функция отклика |
параметр оптимизации |
1 |
|
68 |
2 |
Как называются коэффициенты b0, bj, buj,b jj,…в уравнении регрессии? |
экспериментальные |
выборочные |
теоретические |
оптимальные |
|
2 |
|
69 |
2 |
Как называется коэффициент b0 в уравнении регрессии? |
свободный член уравнения регрессии |
линейный эффект |
квадратичный эффект |
эффект взаимодействия |
фактор |
1 |
|
70 |
2 |
Как называется коэффициент bj в уравнении регрессии? |
свободный член уравнения регрессии |
линейный эффект |
квадратичный эффект |
эффект взаимодействия |
фактор |
2 |
|
71 |
2 |
Как называется коэффициент bjj в уравнении регрессии? |
свободный член уравнения регрессии |
линейный эффект |
квадратичный эффект |
эффект взаимодействия |
фактор |
3 |
|
72 |
2 |
Как называется коэффициент buj в уравнении регрессии? |
свободный член уравнения регрессии |
линейный эффект |
квадратичный эффект |
эффект взаимодействия |
фактор |
4 |
|
73 |
2 |
Укажите условие метода наименьших квадратов |
N-l |
|
|
|
|
2 |
|
74 |
2 |
Как найти число степеней свободы выборки |
N-l |
|
|
|
|
1 |
|
75 |
2 |
Из какого выражения находятся коэффициенты в уравнении регрессии? |
N-l |
|
|
|
|
2 |
|
76 |
2 |
Как называется разность между объемом выборки и числом связей, наложенных на эту выборку? |
уравнением регрессии |
числом степеней свободы |
параметром оптимизации |
функцией отклика |
оптимумом |
2 |
|
77 |
2 |
По чему подбирают уравнение регрессии? |
виду уравнения регрессии |
виду эмпирической линии регрессии |
виду параметров уравнения регрессии |
по виду поля корреляции |
|
2 |
|
78 |
2 |
Чему равно число коэффициентов в уравнении регрессии? |
числу связей, наложенных на выборку |
числу степеней свободы выборки |
объему выборки |
порядку уравнения |
числу параметров |
1 |
|
79 |
2 |
Чему равно количество уравнений в системе нормальных уравнений? |
числу связей, наложенных на выборку |
числу степеней свободы выборки |
числу коэффициентов в уравнении регрессии |
порядку уравнения |
числу параметров |
3 |
|
80 |
2 |
Выполнение каких равенств является необходимым условием минимума функции Ф (b0, b1, …) |
|
|
|
|
|
13 |
|
81 |
2 |
Сколько коэффициентов содержит уравнение регрессии, если в системе нормальных уравнений 5 уравнений? |
4 |
6 |
5 |
3 |
2 |
3 |
|
82 |
2 |
Сколько коэффициентов содержит уравнение регрессии, если число связей равно3? |
3 |
4 |
2 |
1 |
5 |
1 |
|
83 |
2 |
Сколько входит уравнений в систему нормальных уравнений параболической регрессии? |
1 |
2 |
3 |
4 |
5 |
3 |
|
84 |
2 |
Сколько уравнений содержит система нормальных уравнений в линейной регрессии от одного параметра? |
1 |
2 |
3 |
4 |
5 |
2 |
|
85 |
2 |
Что вычисляется для оценки силы линейной связи? |
выборочный коэффициент регрессии |
теоретический коэффициент регрессии |
выборочный коэффициент корреляции |
коэффициент множественной корреляции |
параметр оптимизации |
3 |
|
86 |
2 |
Что вычисляется для оценки силы связи в случае множественной регрессии? |
выборочный коэффициент регрессии |
теоретический коэффициент регрессии |
выборочный коэффициент корреляции |
коэффициент множественной корреляции |
параметр оптимизации |
4 |
|
87 |
2 |
Как найти коэффициент b0 в линейной регрессии от одного параметра? |
|
|
|
|
|
12 |
|
88 |
2 |
Как найти коэффициент b1 в линейной регрессии от одного параметра? |
|
|
|
|
|
3 |
|
89 |
2 |
Как найти выборочный коэффициент корреляции в линейной регрессии от одного параметра? |
|
|
|
|
|
4 |
|
90 |
2 |
Как определить выборочные дисперсии при определении однородности дисперсии? |
|
|
|
|
|
5 |
|
91 |
2 |
В случае если дисперсии однородны, то … |
Gmax=Gp(N,m-1) |
Gmax<Gp(N,m-1) |
Gmax>Gp(N,m-1) |
|
|
2 |
|
92 |
2 |
Уравнение регрессии адекватно, если |
F=Fp(f1;f2) |
F>Fp(f1;f2) |
F<Fp(f1;f2) |
|
|
3 |
|
93 |
2 |
Как найти критерий Фишера, чтобы проверить адекватность уравнения регрессии? |
|
|
|
|
|
1 |
|
94 |
2 |
Систему каких уравнений необходимо решить при вычислении коэффициентов трансцендентной регрессии? |
линейных |
нелинейных |
нормальных |
квадратичных |
|
2 |
|
95 |
2 |
Как расшифровать sост? |
остаточная дисперсия |
оставшаяся дисперсия |
дисперсия остатка |
остаточный коэффициент |
|
1 |
|
96 |
2 |
Как обозначается выборочный коэффициент корреляции в линейной регрессии? |
|
R |
s |
si2 |
ti |
1 |
|
97 |
2 |
Как обозначается коэффициент множественной корреляции? |
|
R |
s |
si2 |
ti |
2 |
|
98 |
2 |
Как обозначаются критерии Стьюдента в линейной регрессии? |
|
R |
s |
si2 |
ti |
5 |
|
99 |
2 |
Как обозначаются выборочные дисперсии? |
|
R |
s |
si2 |
ti |
4 |
|
100 |
2 |
Силу связи можно
характеризовать величиной
|
|
|
|
|
|
1 |
|
101 |
2 |
Как находится корреляционное отношение? |
|
|
|
|
|
1 |
|
102 |
2 |
Что характеризует корреляционное отношение? |
тесноту связи между случайными величинами |
зависимость между переменными |
условия оптимума |
результаты эксперимента |
|
1 |
|
103 |
2 |
Чему равно корреляционное отношение в случае линейной регрессии? |
выборочному коэффициенту корреляции |
коэффициенту множественной корреляции |
величине
|
критерию Фишера |
критерию Кохрена |
1 |
|
104 |
2 |
Переходя от натурального масштаба к новому в методе множественной корреляции проводят … всех значений случайных величин |
нормировку |
анализ |
корректировку |
компановку |
статистику |
1 |
|
105 |
2 |
Формула для нахождения коэффициента множественной регрессии имеет вид… |
|
|
|
|
|
1 |
|
106 |
2 |
По какой формуле перейти от натурального масштаба к новому для значения у1? |
|
|
|
|
|
1 |
|
107 |
2 |
Формула для нахождения скорректированного значения коэффициента множественной корреляции имеет вид… |
|
|
|
|
|
4 |
|
108 |
2 |
Сколько вершин имеет k- мерный симплекс? |
k |
k+1 |
k-1 |
k+2 |
k-2 |
2 |
|
109 |
2 |
Сколько граней расположено против вершины симплекса? |
0 |
1 |
2 |
3 |
4 |
2 |
|
110 |
2 |
Сколько вершин нового симплекса отличается расположением от предыдущего? |
0 |
1 |
2 |
3 |
4 |
2 |
|
111 |
2 |
Высота правильного k-мерного симплекса равна… |
|
|
|
|
|
1 |
|
112 |
2 |
Число опытов в симплексной матрице для k независимых факторов равно… |
N= k+1 |
N= k |
N= k+j |
N=j+1 |
|
1 |
|
113 |
2 |
Чему равно число опытов в симплексном плане, если число коэффициентов в уравнении регрессии равно 5? |
2 |
3 |
4 |
5 |
6 |
4 |
|
114 |
2 |
Какая точка в симплексном методе заменяется «зеркальным отображением»? |
наилучшая |
наихудшая |
начало координат |
противоположная |
|
2 |
|
115 |
2 |
Сколько вершин имеет симплекс в 4-х-мерном пространстве? |
3 |
4 |
5 |
2 |
6 |
3 |
|
116 |
2 |
Как записывается уравнение регрессии по методу Брандона? |
|
|
|
|
|
1 |
|
117 |
2 |
Как найти дисперсию коэффициентов для симплексного плана? |
|
|
|
|
|
12 |
|
118 |
2 |
Коэффициенты регрессии в симплексном методе находятся по формуле… |
|
|
|
|
|
1 |
|
119 |
2 |
Планирование эксперимента в условиях крупномасштабных производств осуществляется при помощи…планирования |
эволюционного |
оптимального |
симплексного |
случайного |
производственного |
1 |
|
120 |
2 |
К натуральному масштабу в методе множественной корреляции необходимо перейти по формулам… |
(j=1…k) |
|
|
|
|
12 |

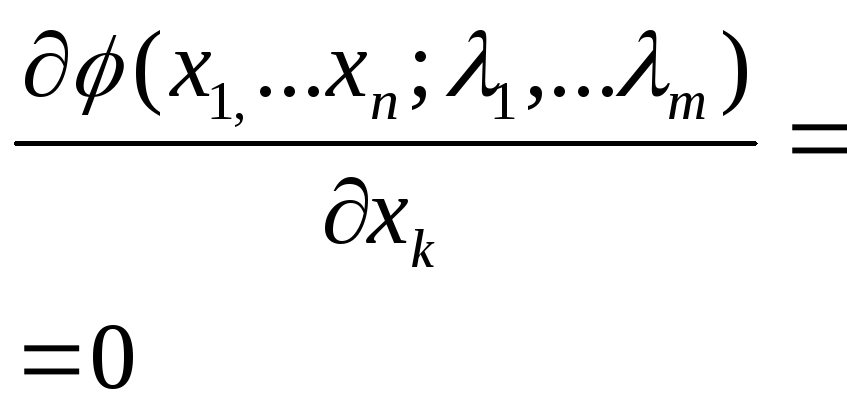
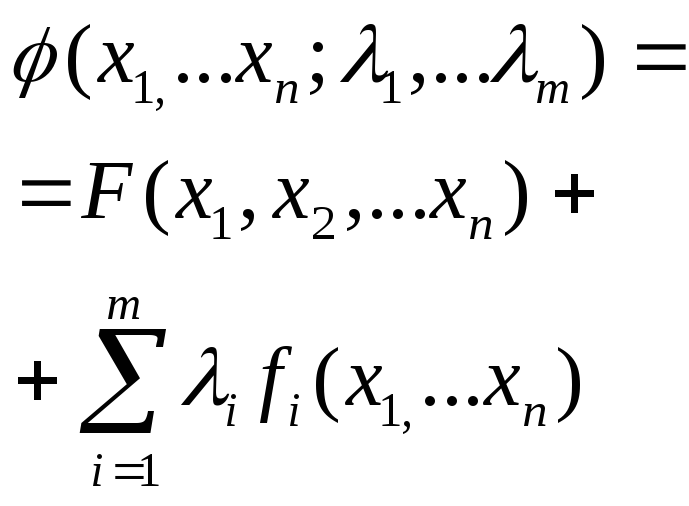
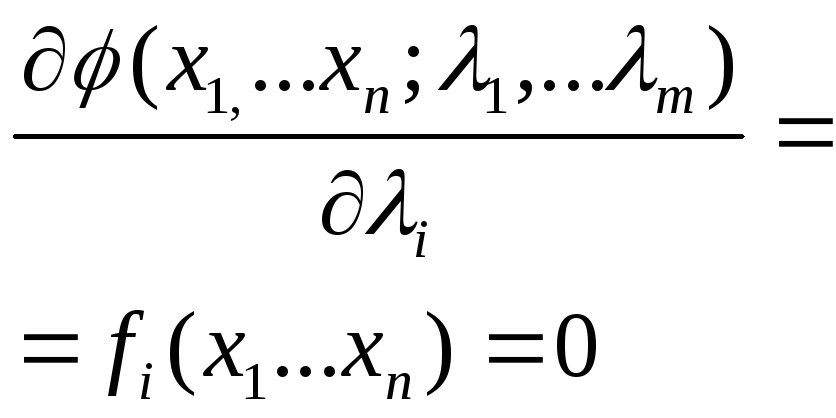
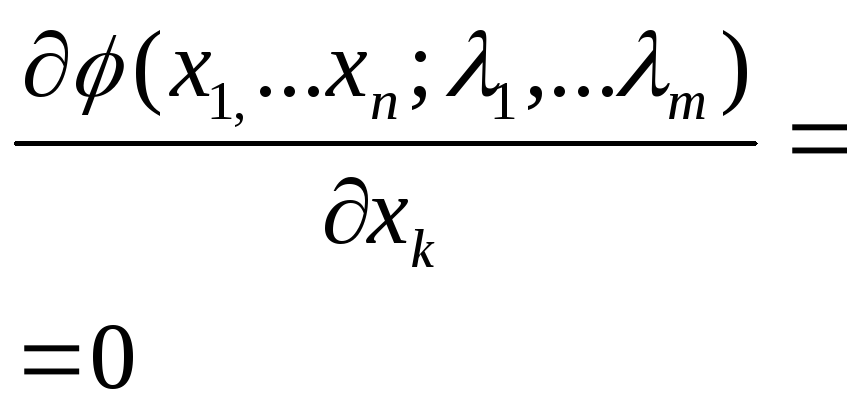
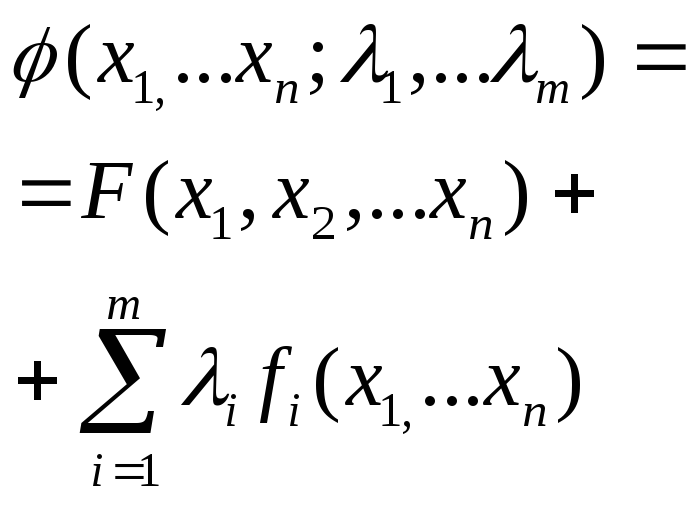
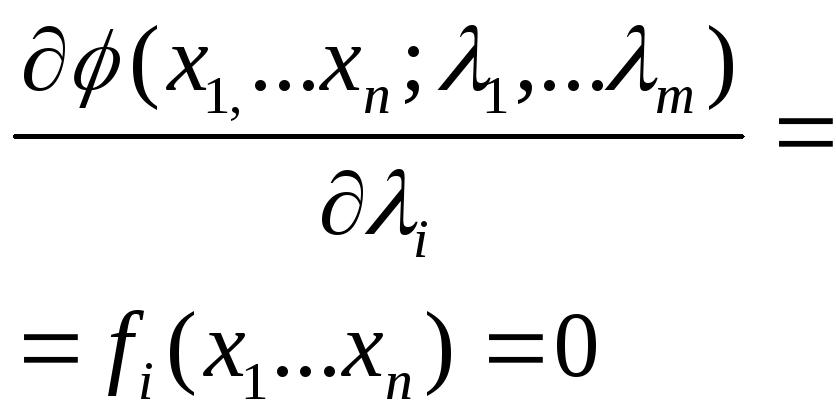
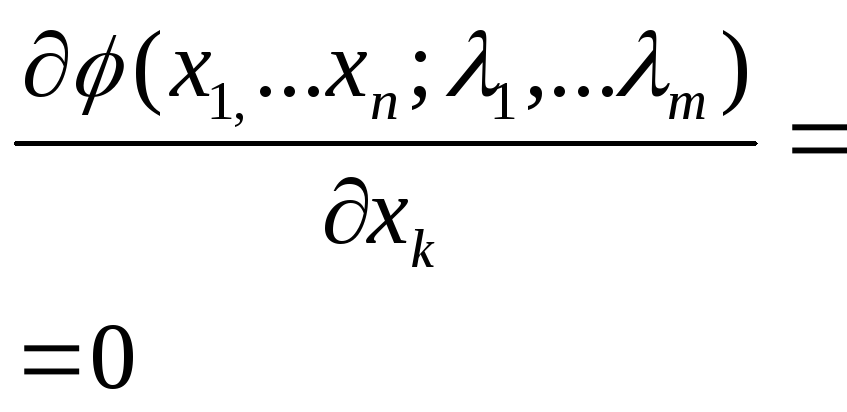
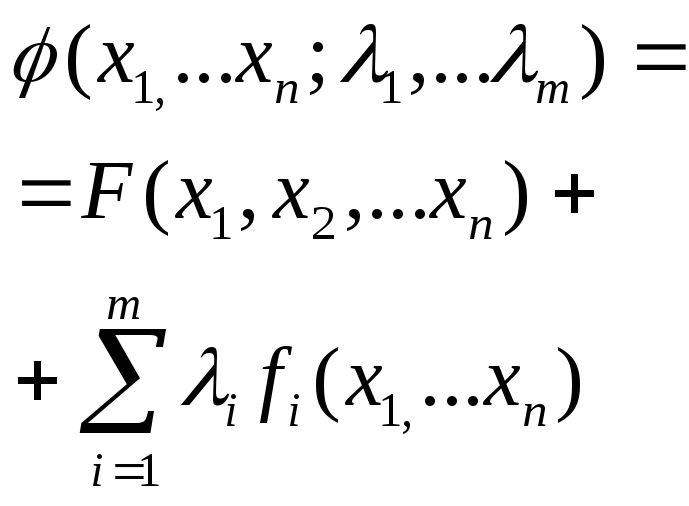
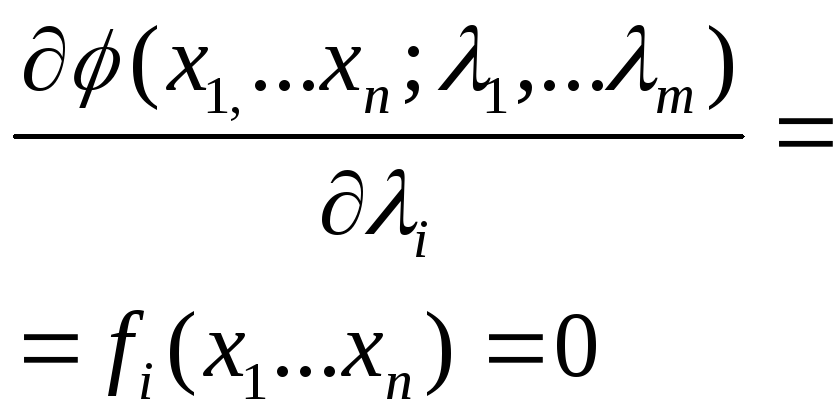
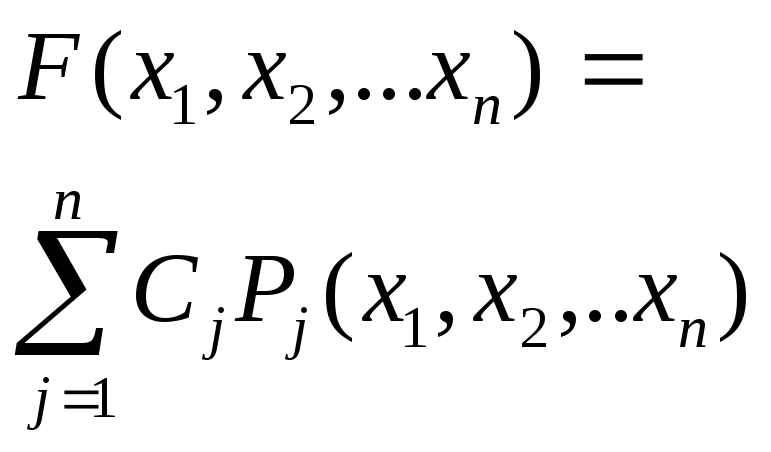
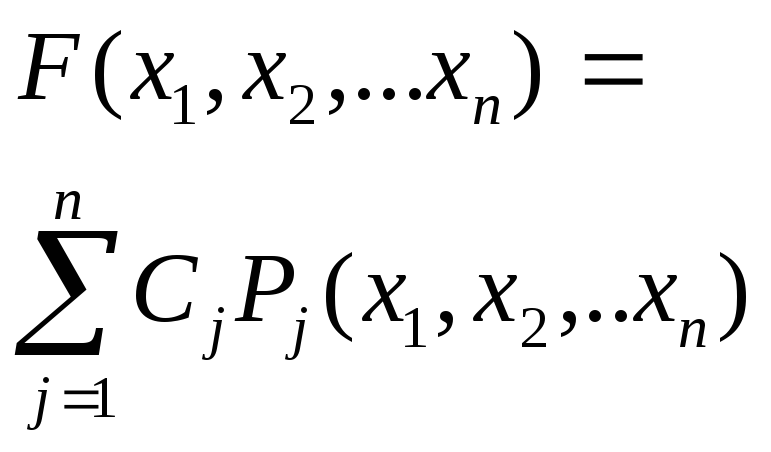
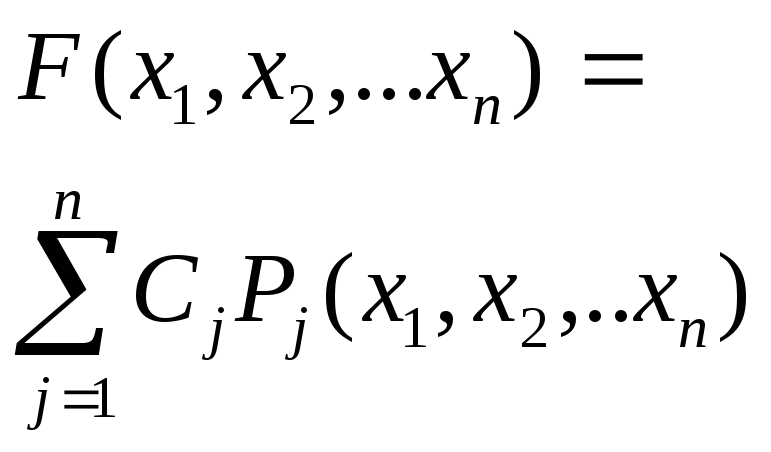
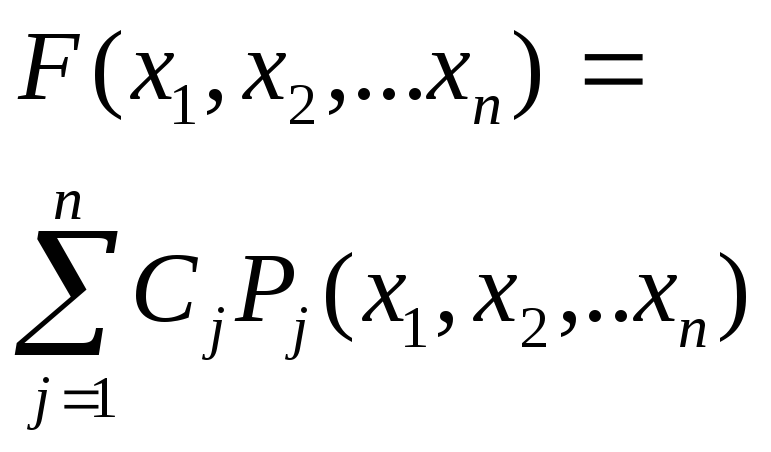
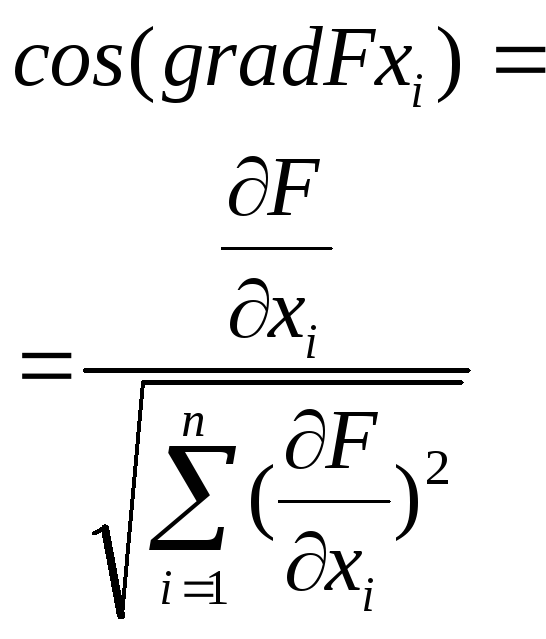
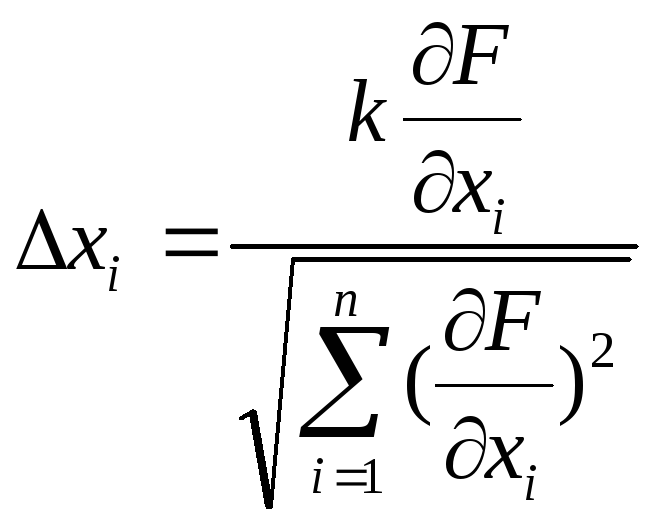
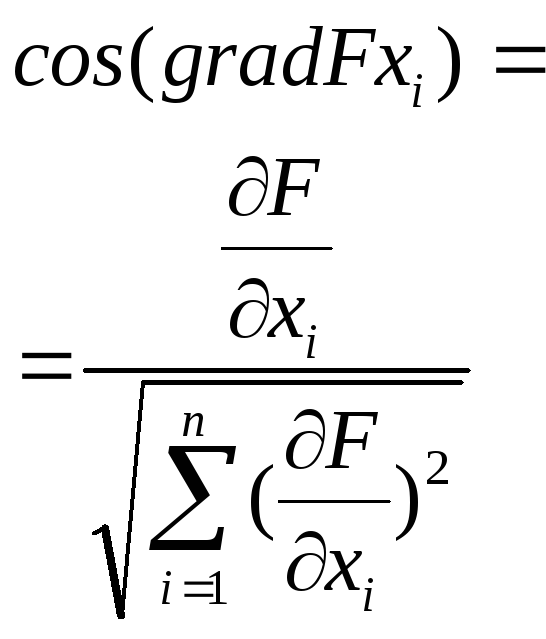
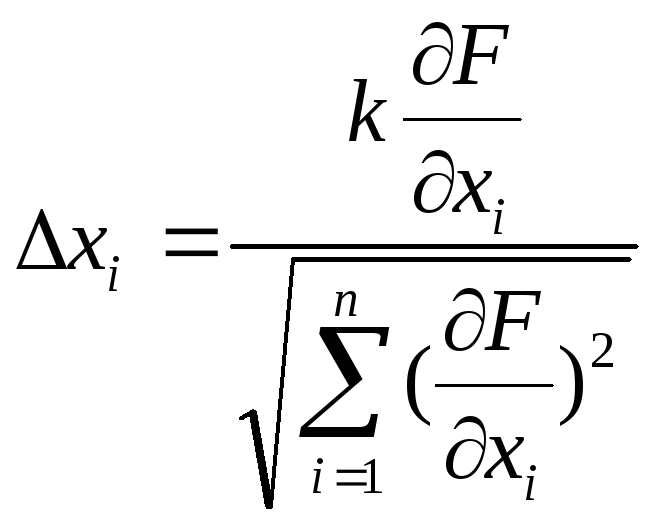
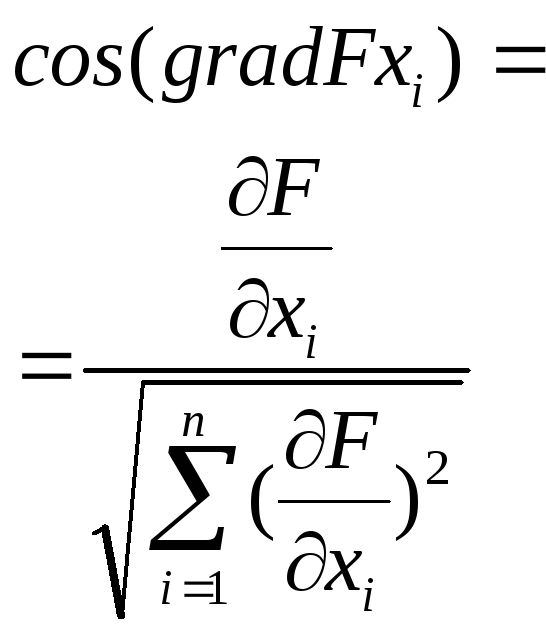

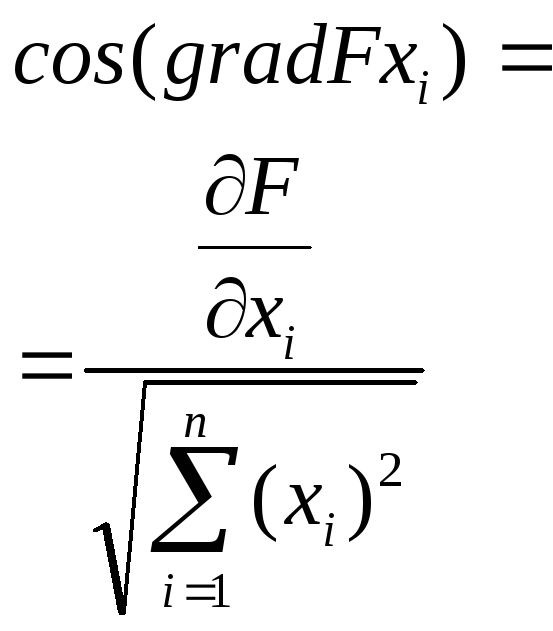
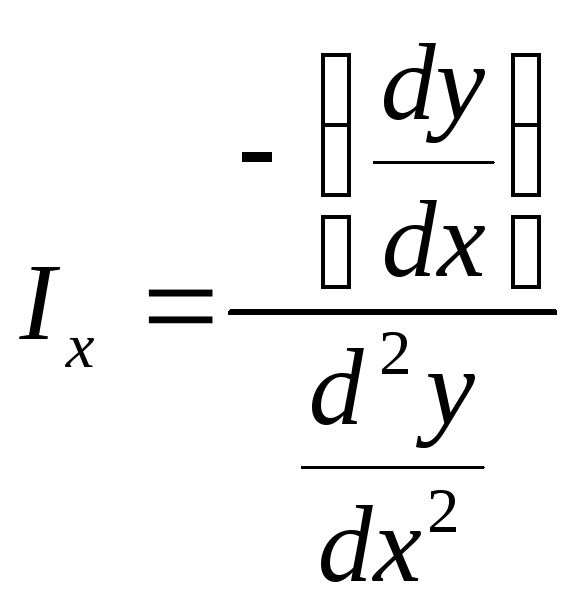
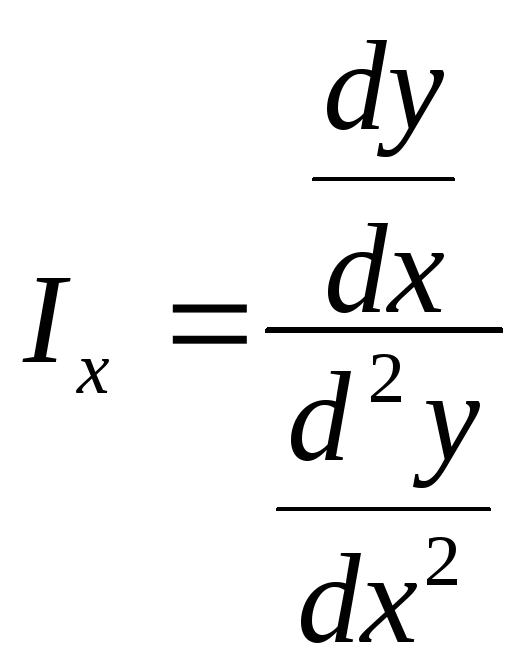
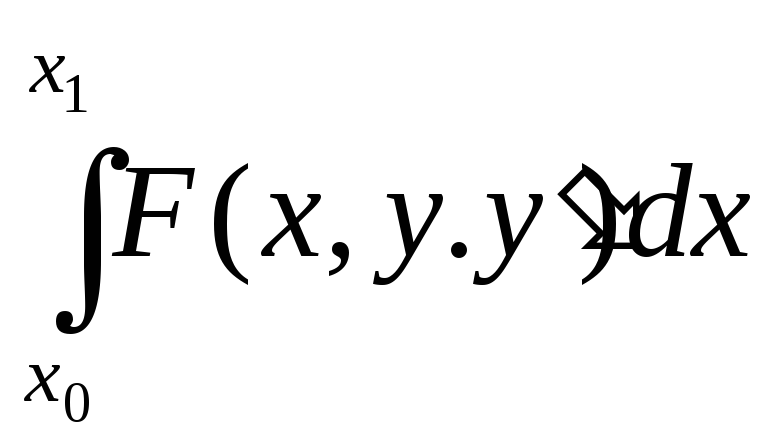
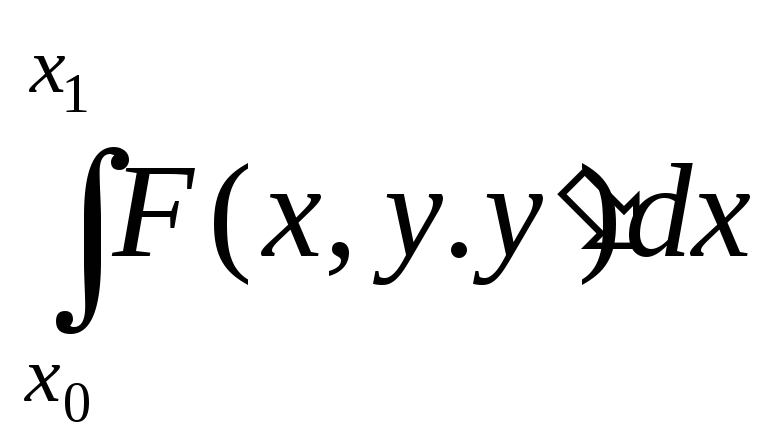
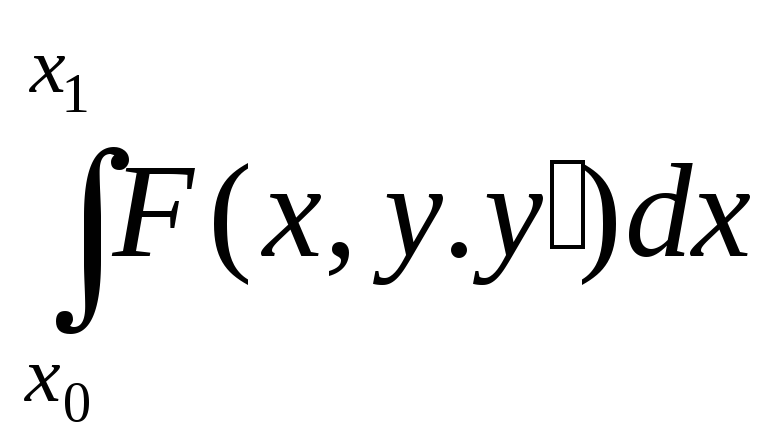
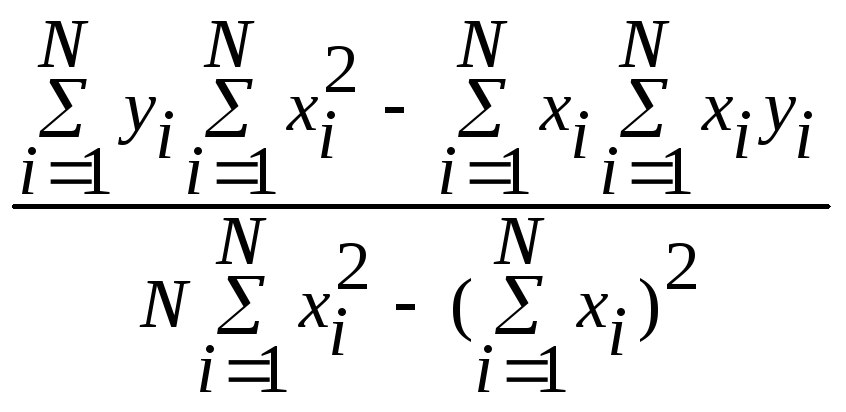
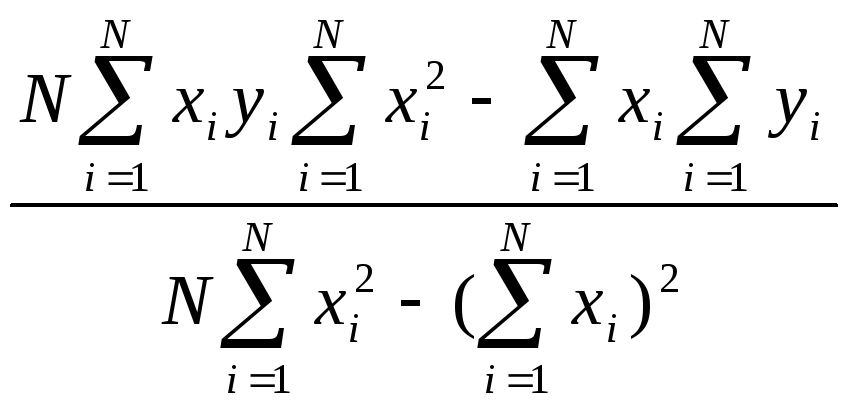
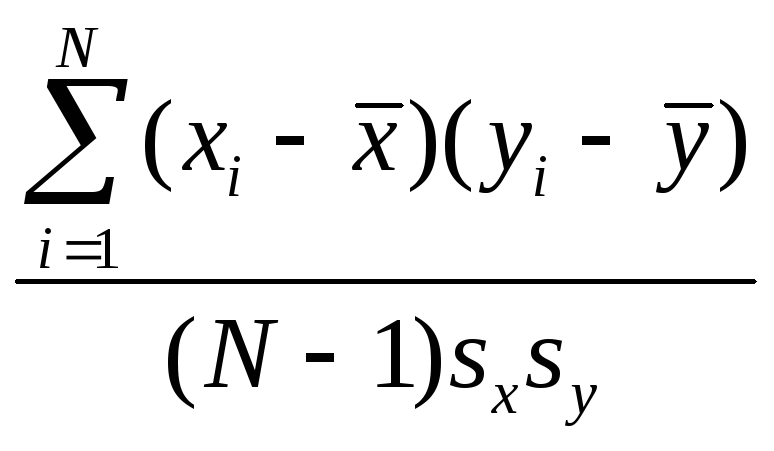
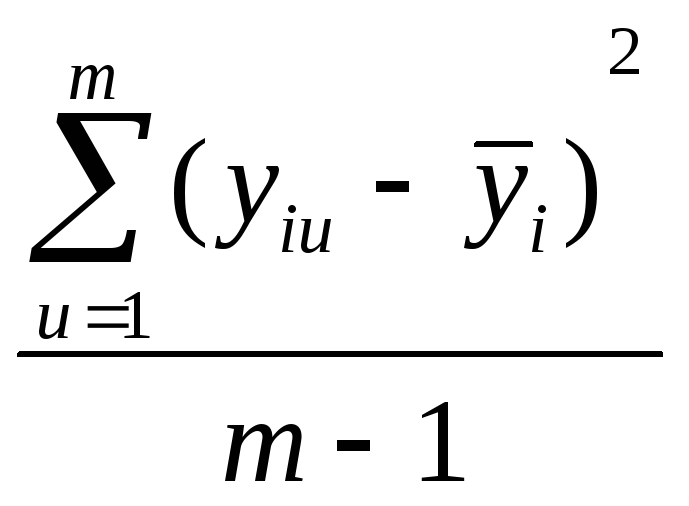
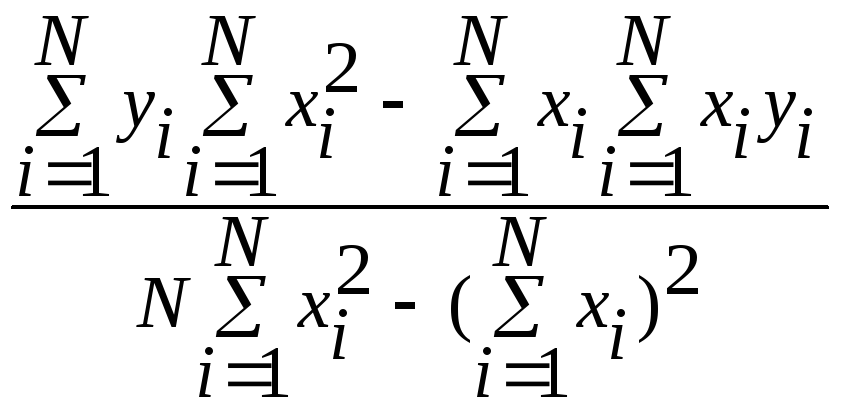
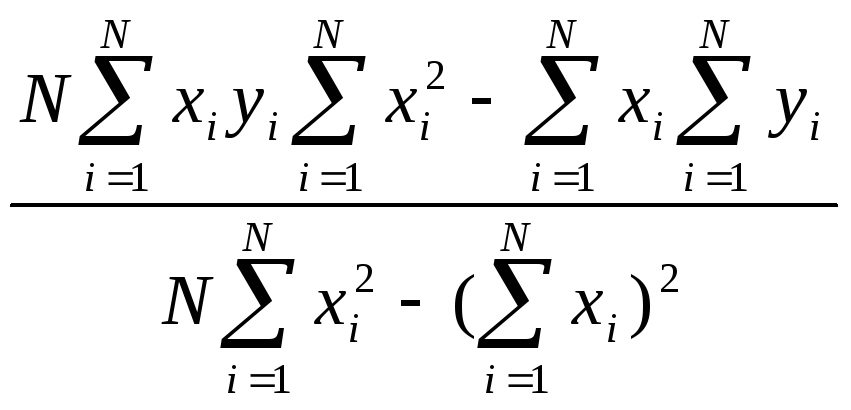
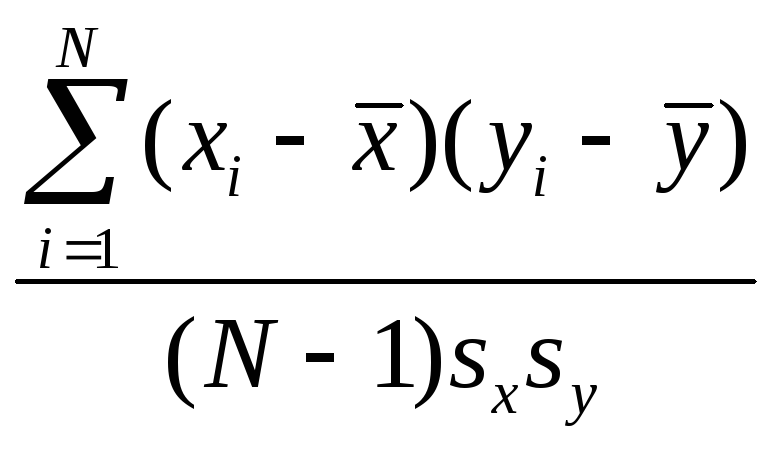
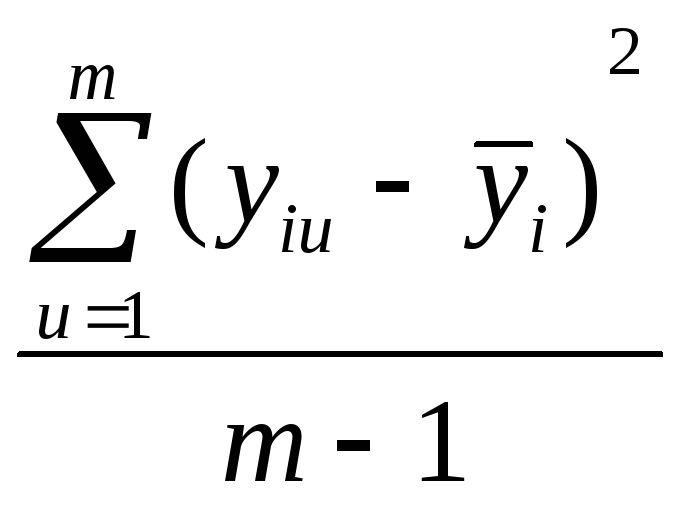
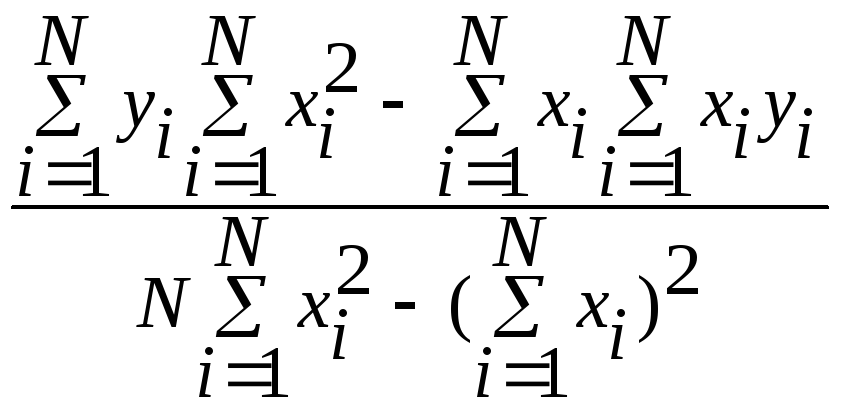
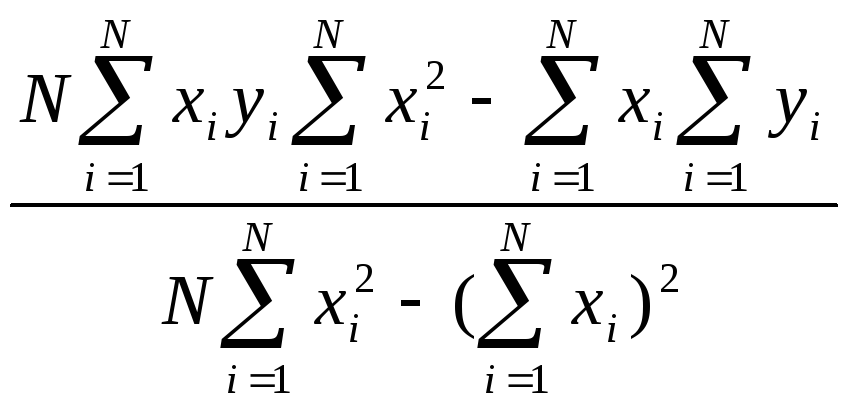
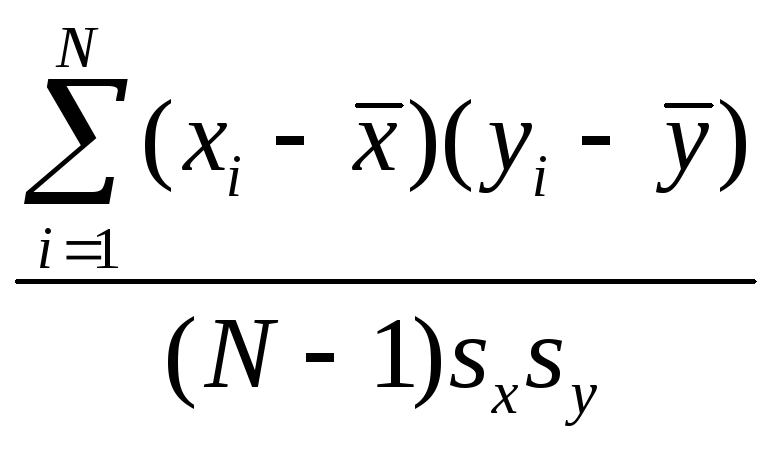
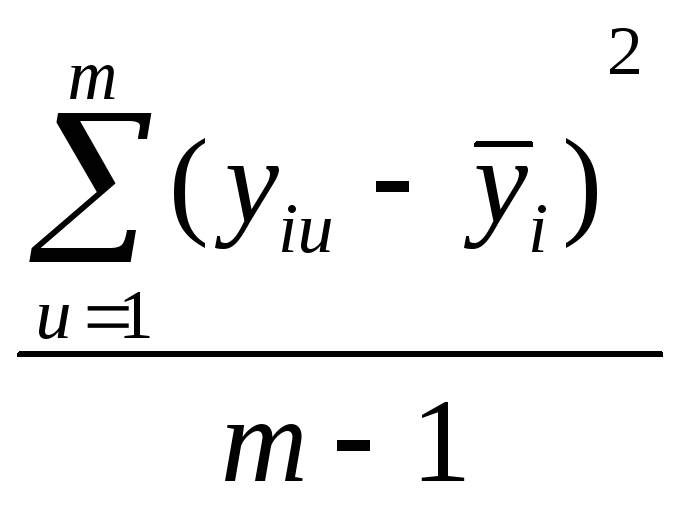
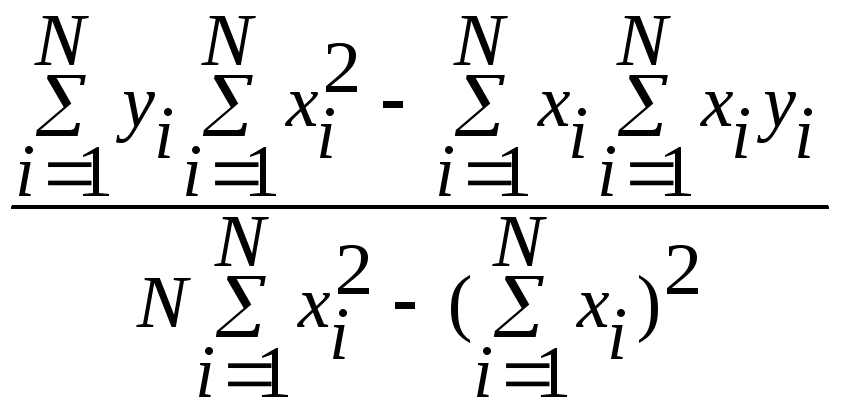
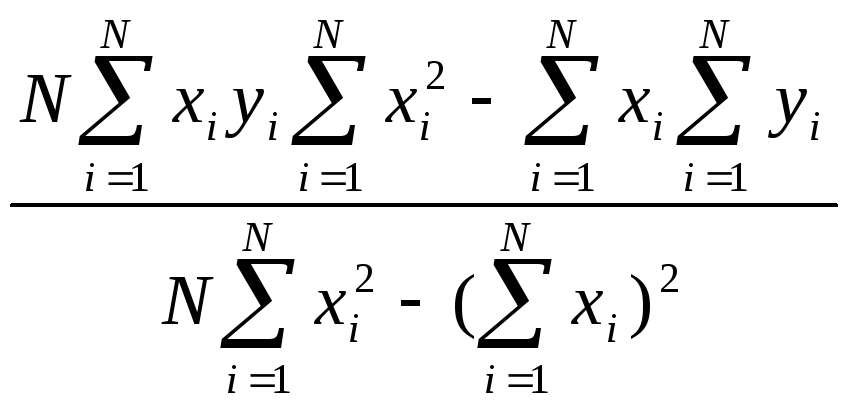
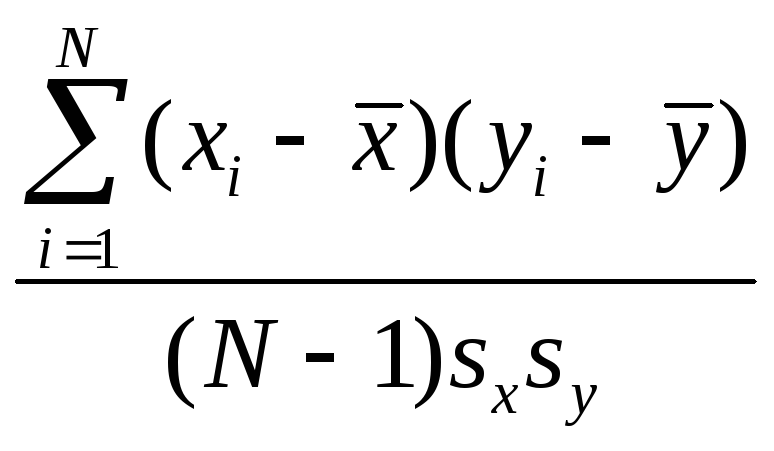
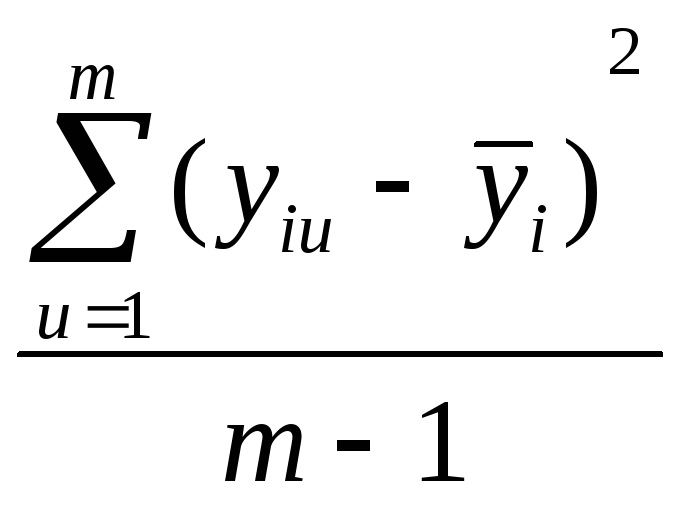
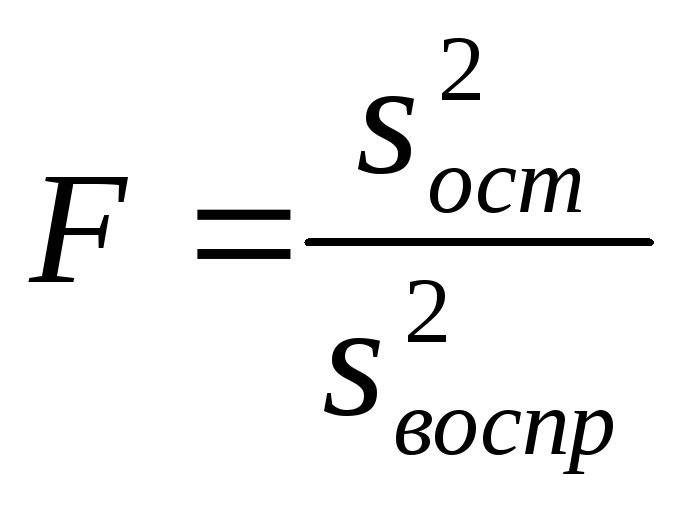
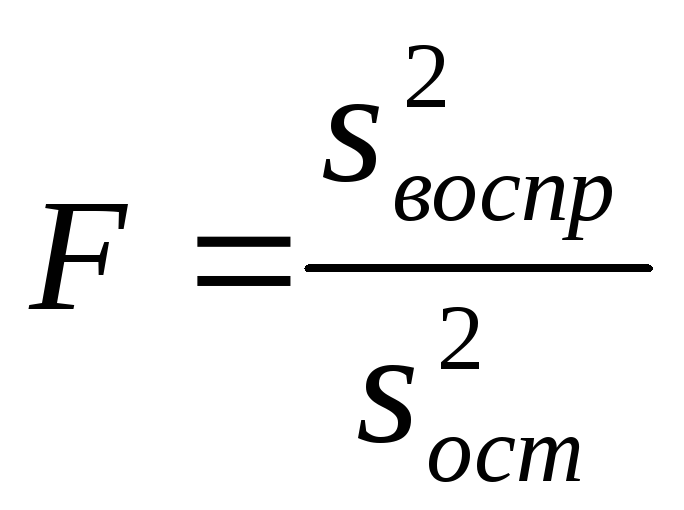
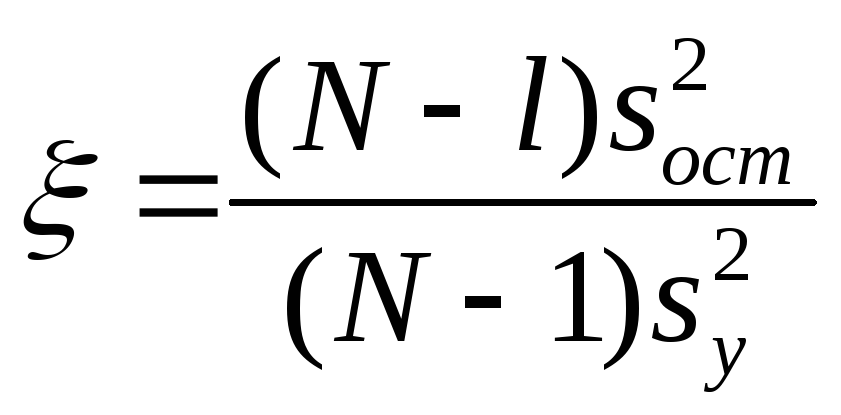
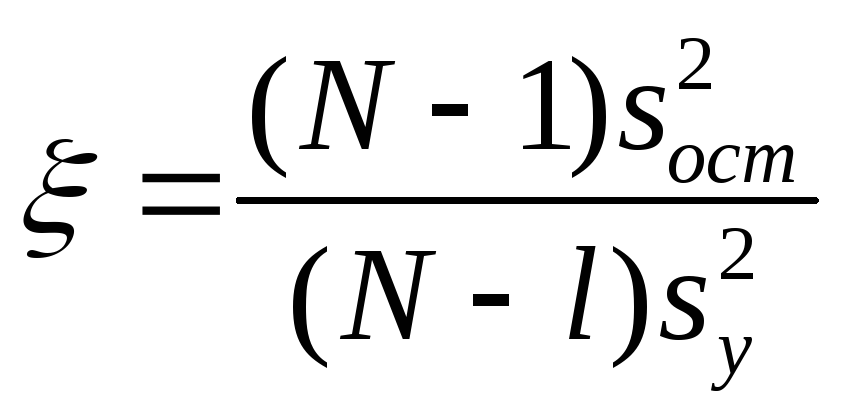
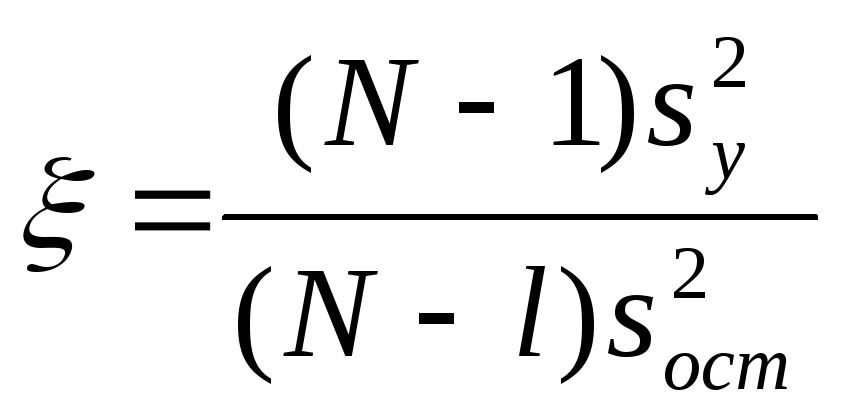
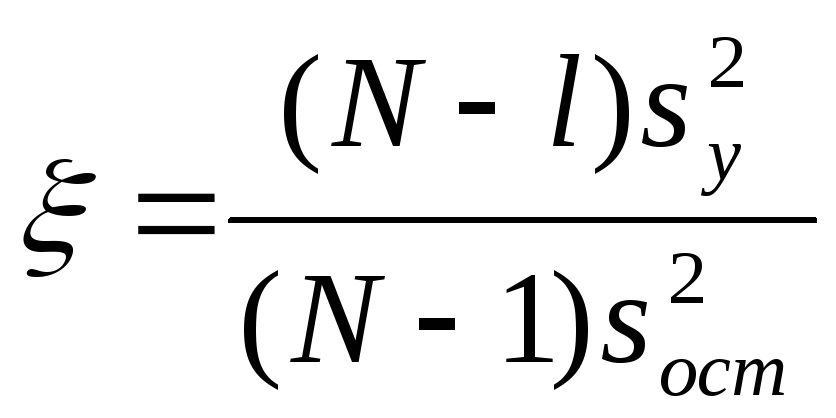
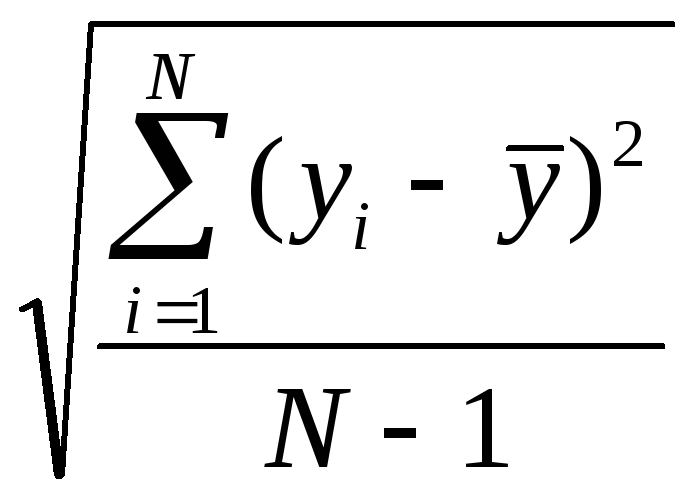
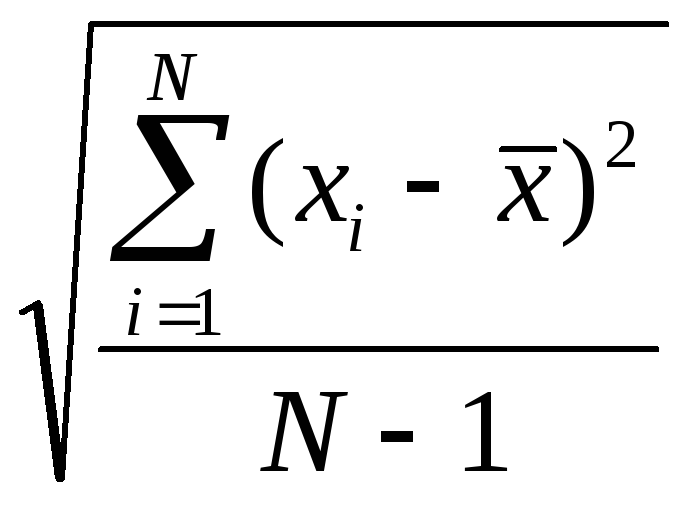
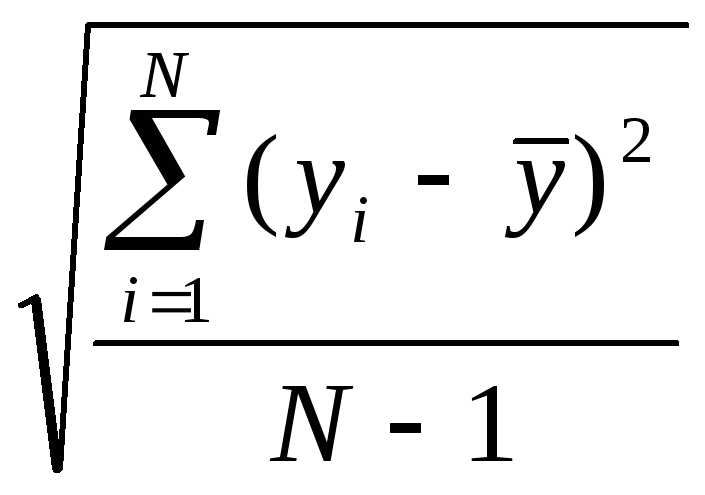

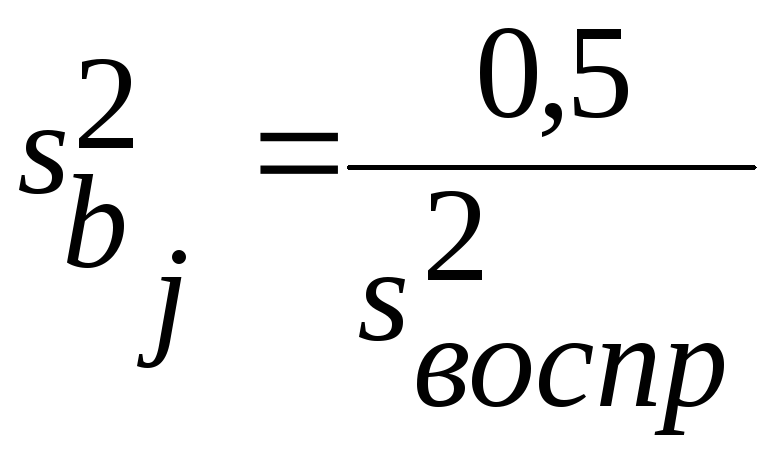
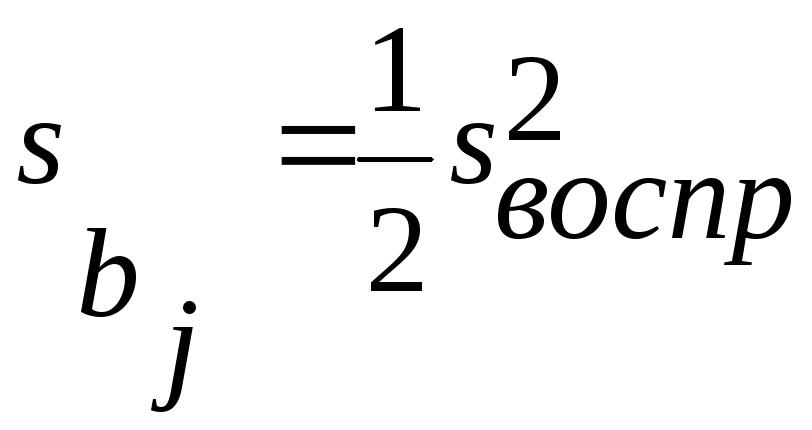
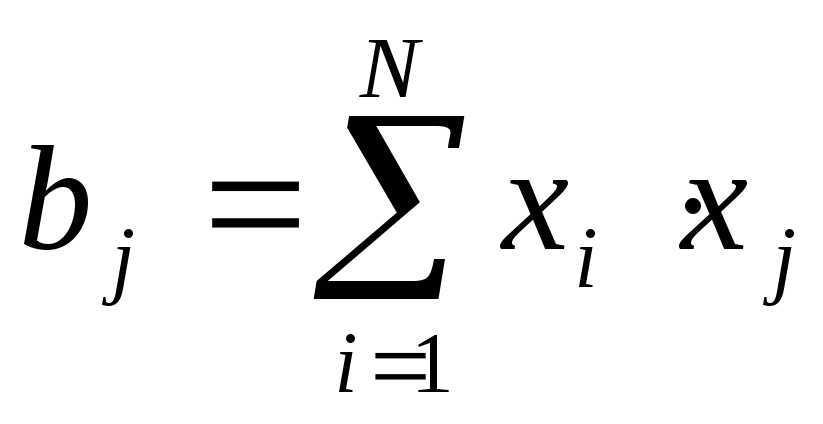 (j=1…k)
(j=1…k)