Базы / АТПиП лаба2 Камалтдинова Л.Л

МИНИМСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РТ

альметьевский государственный нефтяной институт

Кафедра АИТ

Лабораторная работа №2

Тема: «Расчет настройки каскадной САР методом незатухающих колебаний и оценка качества процессов регулирования»

Вариант 9

Выполнил:

студент группы 32-61

Камалтдинова Л.Л.

Проверил: ст. преподаватель

Орехова Л.Г.

Альметьевск 2015г.

1. Теоретическая часть.

Для повышения качества регулирования объектов с существенными инерционными свойствами и большим запаздыванием применяют каскадные САР.

Применение каскадной САР возможно в случае, если:

• имеется промежуточная регулируемая переменная , зависящая от того же самого регулирующего воздействия , что и основная регулируемая переменная (рис. 1. 1.);

• промежуточный канал регулирования является более быстродействующим, чем основной канал , т. е. рабочая частота регулятора промежуточной переменной выше рабочей частоты регулятора основной переменной.

На рис. 1. 1. Приняты следующие обозначения:

- вход объекта;

- основной регулируемый параметр;

- вспомогательный (промежуточный) регулируемый параметр;

- передаточная функция объекта по основному каналу;

- передаточная функция объекта по промежуточному каналу.

Предполагается, что возмущение действует по тому же каналу, что и регулирующее воздействие регулятора.

Структурная схема каскадной САР приведена на рис. 1.2. Регулятор является стабилизирующим (внутренним, вспомогательным), регулятор - корректирующим (внешним, основным). Регулирующее воздействие, вырабатываемое регулятором , является заданием регулятору .

Рис. 1. 1. Схема объекта регулирования.

. Рис. 1. 2. Структурная схема каскадной САР:

- регулирующее воздействие регулятора ;

- регулирующее воздействие регулятора .

Рис. 1.3. Каскадная система регулирования температуры на выходе рибойлера.

- регулятор температуры (основной );

- регулятор расхода (вспомогательный ).

Типичными примерами каскадных систем являются:

система регулирования температуры на выходе из рибойлера установки подготовки нефти и установки осушки газа с дополнительным воздействием по расходу пара (рис. 1. 3.);

система регулирования температуры на выходе трубчатой печи с дополнительным воздействием по температуре над перевальной стенкой;

система регулирования уровня в колоннах с дополнительным воздействием по расходу уходящего продукта.

2. Расчет параметров настройки регуляторов.

Расчет параметров настройки регуляторов и каскадной CAP осуществляется теми же методами, что и расчет настроек регулятора одноконтурной САР.

При этом двухконтурную каскадную систему (рис. 1.2) представля­ют в виде сочетания двух одноконтурных систем, в состав которых входят так называемые “эквивалентные объекты”.

Передаточная функция эквивалентного объекта в одноконтурной САР с регулятором (рис. 1. 4) определяется выражением:

. (2. 1)

При различной инерционности основного и промежуточного каналов первым членом правой части выражения (2.1) можно пренебречь.

Сравнение инерционности основного и промежуточного каналов производится на основании выполнения условия

. (2. 2)

В этом случае передаточная функция эквивалентного объекта для регулятора равна:

. (2. 3)

Рис. 1. 4. Структурная схема одноконтурной САР с регулятором .

Рис. 1. 5. Структурная схема одноконтурной CAP с регулятором .

Передаточная функция эквивалентного объекта в одноконтурной САР с регулятором (рис. 1.5) определяется выражением:

. (2. 4)

Если на рабочей частоте выполняется условие

, (2. 5)

то передаточная функция эквивалентного объекта для регулятора равна

. (2. 6)

При выполнении условия расчёт параметров настройки регуляторов каскадной САР осуществляется в следующем порядке:

1. Определяется передаточная функция эквивалентного объекта для основного регулятора по формуле (2. 6).

2. Рассчитываются настройки регулятора .

3.Рассчитываются настройки внутреннего регулятора , эквивалентный объект для которого определён формулой (2. 3).

4. Проверяется условие (2. 2). В случае его выполнения расчёт настроек регуляторов и считается законченным.

В противном случае настройки регуляторов уточняются для передаточных функций эквивалентных объектов, определяемых формулами (2. 1) и (2. 4).

3. Расчет параметров настройки регуляторов методом незатухающих колебаний (метод Циглера-Никольса).

Как и в предыдущем методе расчета, исходными данными являются передаточная функция регулятора с неизвестными параметрами.

Расчет производится в два этапа.

1. Расчет критической настройки П1_кр пропорциональной составляющей регулятора (П2=П3=0), при САР находится на границе устойчивости.

2. Определение по П1_кр рабочих настроек регуляторов по приближенным формулам.

Метод обеспечивает для большинства объектов степень затухания переходного процесса 0,75 и небольшую динамическую ошибку.

Определение П1_кр.

Как известно, замкнутая САР находится на границе устойчивости, если разомкнутая система устойчива и ее АФХ проходит через точку с координатами (-1;j0). Это условие, выполняемое на частоте _кр, называется критической, имеет вид:

(1.25)

Так как

(1.26)

то уравнение (1.25) можно представить как систему двух уравнений:

(1.27)

АФХ П-регулятора известна:

(1.29)

Из второго уравнения системы (1.29) находим _кр, из первого П1_кр:

(1.30)

Определение рабочих настроек регуляторов.

П-регулятор:

(1.31)

ПИ-регулятор:

(1.32)

ПИД-регулятор:

(1.33)

Задача:

Исходные данные:

- передаточная функция по основному каналу;

- передаточная функция по промежуточному каналу;

Рассчитать параметры настройки основного и промежуточного регуляторов.

Необходимо рассчитать параметры основного и промежуточного каналов. В качестве первого регулятора Р1 выбираем П - регулятор, а в качестве второго Р2 – ПИ-регулятор.

1. Определим передаточную функцию эквивалентного объекта для ПИ-регулятора (Р2):

2. Определяем настройки регулятора Р2 методом Циглера - Никольса. АФХ эквивалентного объекта в показательной форме:

Определим критическое значение параметра настройки регулятора. Система уравнений для расчета П1кр и ωкр имеет вид:

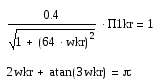
Из второго уравнения этой системы найдем ω_кр :

Подставим значение ω_кр = 0,581 первое уравнение системы и вычислим значение П1_кр:

Настроечные параметры регулятора Р2 равны:

3. Определяем настройки регулятора Р1 методом Циглера - Никольса:

АФХ эквивалентного объекта в показательной форме:

Определим критическое значение параметра настройки регулятора.

Система уравнений для расчета П2кр и ω2кр имеет вид:

Из второго уравнения этой системы найдем ωкр :

Подставим значение ω_2кр=1,224 в первое уравнение системы и вычислим значение П2_кр:

Настроечные параметры регулятора Р1 равны:

4. Проверим правильность выполнения условия:

Найдем численное значение правой части неравенства:

Найдем численное значение левой части неравенства:

Неравенство подтвердилось, так как:

3. Моделирование на ЭВМ

1. Одноконтурной САР

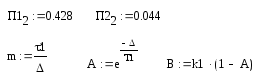
2. Каскадной САР

Сравнительный анализ качества ПП в исследуемых САР

Прямые показатели качества переходных процессов	Каскадная система	Одноконтурная система
Время переходного процесса tП	152	390
Статическая ошибка δстат	0	0
Максимальное отклонение в переходный период	0.28	1.2
Время достижения максимума tmax	40	38
Время запаздывания	3	9

Вывод

По результатам таблицы сравнения качества двух переходных процессов, видно, что применение каскадной САР является целесообразным, так как:

1. Максимальное отклонение за время переходного процесса у каскадной САР оказалось во много раз меньше, чем у одноконтурной (0,28 < 1.2).

2. Интегральная оценка каскадной САР больше чем у одноконтурной (0.215 > 0,032).

3. Время переходного процесса у каскадной САР намного меньше, чем у одноконтурной (152 < 390).

13